数据结构和算法：“变位词”判断问题

“变位词”判断问题

❖问题描述

所谓“变位词”是指两个词之间存在组成字母的重新排列关系

如：heart和earth，python和typhon 为了简单起见，假设参与判断的两个词仅由小写 字母构成，而且长度相等

❖解题目标：

写一个bool函数，以两个词作 为参数，返回这两个词是否变位词

❖可以很好展示同一问题的不同数量级算法

变位词解法：

解法1：逐字检查

❖解法思路

      将词1中的字符逐个到词2中检查是否存在 存在就“打勾”标记（防止重复检查） 如果每个字符都能找到，则两个词是变位词 只要有1个字符找不到，就不是变位词

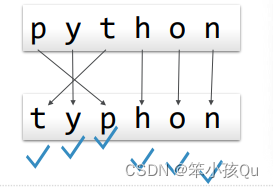
❖程序技巧

实现“打勾”标记：将词2对应字符设为None 由于字符串是不可变类型，需要先复制到列表中

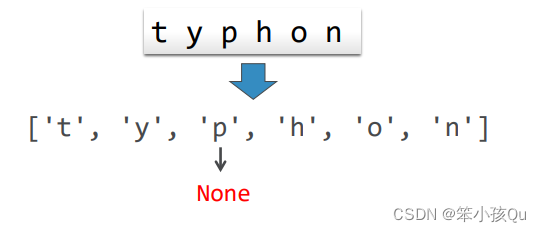
 ❖程序代码

❖算法分析

❖问题规模：词中包含的字符个数n

❖主要部分在于两重循环

      外层循环遍历s1每个字符，将内层循环执行n次

       而内层循环在s2中查找字符，每个字符的对比次 数，分别是1、2…n中的一个，而且各不相同

❖所以总执行次数是1+2+3+……+n

可知其数量级为O(n^2)

解法2：排序比较

 ❖解题思路

     将两个字符串都按照字母顺序排好序 再逐个字符对比是否相同，如果相同则是变位词 有任何不同就不是变位词

 ❖程序代码

❖算法分析

❖粗看上去，本算法只有一个循环，最多执 行n次，数量级是O(n)

       但循环前面的两个sort并不是无代价的 如果查询下后面的章节，会发现排序算法采用不 同的解决方案，其运行时间数量级差不多是 O(n2)或者O(n log n)，大过循环的O(n)

❖所以本算法时间主导的步骤是排序步骤

❖本算法的运行时间数量级就等于排序过程 的数量级O(n log n)

解法3：暴力法

❖暴力法解题思路为：穷尽所有可能组合

❖将s1中出现的字符进行全排列，再查看s2 是否出现在全排列列表中

❖这里最大困难是产生s1所有字符的全排列 根据组合数学的结论，如果n个字符进行全排列 ，其所有可能的字符串个数为n!

❖我们已知 n! 的增长速度甚至超过2n

例如，对于20个字符长的词来说，将产生 20!=2,432,902,008,176,640,000个候选词 如果每微秒处理1个候选词的话，需要近8万年时 间来做完所有的匹配。

❖结论：暴力法恐怕不能算是个好算法

 解法4：计数比较

❖解题思路：对比两个词中每个字母出现的 次数，如果26个字母出现的次数都相同的 话，这两个字符串就一定是变位词

❖具体做法：为每个词设置一个26位的计数 器，先检查每个词，在计数器中设定好每 个字母出现的次数

❖计数完成后，进入比较阶段，看两个字符 串的计数器是否相同，如果相同则输出是 变位词的结论

❖程序代码

❖算法分析

❖计数比较算法中有3个循环迭代，但不象 解法1那样存在嵌套循坏

         前两个循环用于对字符串进行计数，操作次数等 于字符串长度n 第3个循环用于计数器比较，操作次数总是26次

❖所以总操作次数T(n)=2n+26，其数量级 为O(n)

         这是一个线性数量级的算法，是4个变位词判断 算法中性能最优的

❖值得注意的是，本算法依赖于两个长度为 26的计数器列表，来保存字符计数，这相 比前3个算法需要更多的存储空间

       如果考虑由大字符集构成的词（如中文具有上万 不同字符），还会需要更多存储空间。

❖牺牲存储空间来换取运行时间，或者相反 ，这种在时间空间之间的取舍和权衡，在 选择问题解法的过程中经常会出现。