LeetCode-Largest Triangle Area

Description：
You have a list of points in the plane. Return the area of the largest triangle that can be formed by any 3 of the points.

Example:

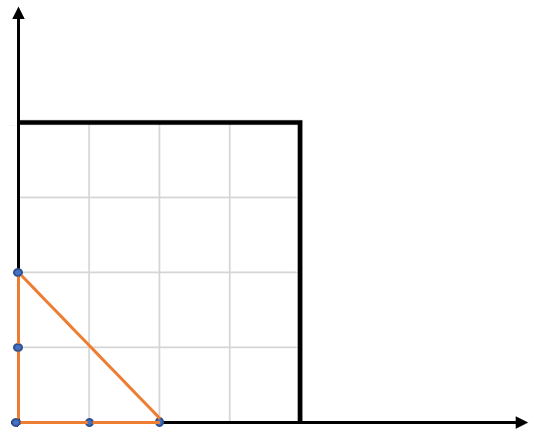
Input: points = [[0,0],[0,1],[1,0],[0,2],[2,0]]
Output: 2
Explanation: 
The five points are show in the figure below. The red triangle is the largest.

Notes:

• 3 <= points.length <= 50.
• No points will be duplicated.
• -50 <= points[i][j] <= 50.
• Answers within 10^-6 of the true value will be accepted as correct.

题意：在坐标轴中，给定一定数量的坐标点(x, y)，要求找出三个点，使这三个点构成的三角形的面积最大；

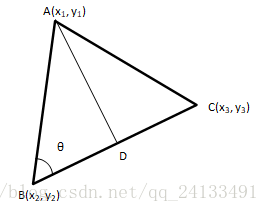
解法：假设我们选取的三个点为A(x₁，y₁)，B(x₂，y₂)，C(x₃，y₃)；D点是过A点作BC的垂线的交点；那么可以得到三角形的面积为：
$$S=\frac{1}{2}|BC||AD|$$
$$S=\frac{1}{2}|BC||BA|sin\theta$$
$$S=\frac{1}{2}|\overrightarrow{BC}\times \overrightarrow{BA}|$$
$$S=\frac{1}{2}|(x_3-x_2,y_3-y_2)\times (x_1-x_2,y_1-y_2)|$$
$$S=\frac{1}{2}|(x_3-x_2)(y_1-y_2)-(y_3-y_2)(x_1-x_2)|$$
$$S=\frac{1}{2}|x_1{y}_2+x_2{y}_3+x_3{y}_1-x_1{y}_3-x_2{y}_1-x_3{y}_2|$$

我们遍历所有可能的组合，返回面积最大的那个；

Java

class Solution {
    public double largestTriangleArea(int[][] points) {
        double result = 0L;
        for (int[] p1 : points)
            for (int[] p2 : points) 
                for (int[] p3 : points) {
                    result = Math.max(result, 0.5 * Math.abs(p1[0] * p2[1] + p2[0] * p3[1] + p3[0] * p1[1] -
                                                             p1[0] * p3[1] - p2[0] * p1[1] - p3[0] * p2[1]));
                }
        return result;
    }
}