590. N叉树的后序遍历

给定一个 N 叉树，返回其节点值的后序遍历。

例如，给定一个 3叉树 :

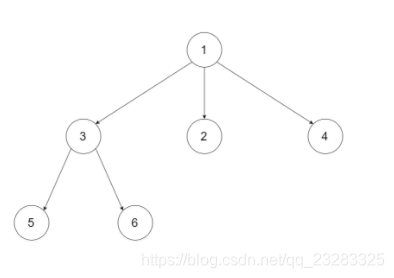
返回其后序遍历: [5,6,3,2,4,1].

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> children;

    Node() {}

    Node(int _val, vector<Node*> _children) {
        val = _val;
        children = _children;
    }
};
*/
class Solution {
public:
    vector<int> postorder(Node* root) {
        vector<int> result;
        if(root == NULL)
            return result;
        bianli(root, result);
        return result;
    }
    void bianli(Node *root, vector<int> &result)
    {
        if(root == NULL) 
            return ;
        for(auto iter : root->children)
            bianli(iter, result);
        result.push_back(root->val);
    }
};