名词定义
- 图:由点集 V 于边集 E 共同构成
- 顶点(vertex);
- 边(edge):用一个点对(v,w)表示,其中的v,w均属于V
- 邻接:w与v邻接,当且仅当 (v,w)属于E;v与w邻接,当且仅当(w,v)属于E
- 权,值:边的一种属性,可视为长度
- 路径:顶点的一个序列
,每个顶点均属于V,且
,路径的长为该序列的边数即n-1;
- 简单路径:所有顶点互异,但首尾可能相同;
- 环:特殊的边(v,v)称作环
- 圈:首尾相同的简单路径,且长度至少为一,如果是无向图,还要求边互异;
- 连通:从任一点出发均存在到达其他点的路径;
- 强连通:满足连通性质的有向图;
- 弱连通:有向图本身不连通,但忽略边的方向后的那个无向图(基础图)是连通的;
- 完全图:任意两点均存在边;
- DAG:有向无圈图(Directed Acyclic Graph)
- Dijkstra算法:有权图的最短路径算法,一种贪婪算法
- 稠密:边的数量相对很多
- 稀疏:边的数量相对很少
- 动作节点图:以节点表示需完成的动作,完成成本(通常是耗时)作为节点的属性,而边无权值。
- 事件节点图:以节点表示某些(可不止一个)动作开始或停止,边表示动作,此时边是有权值的。事件节点图常常会增加一些哑节点(无实际对应)和哑边(权值为0)来做辅助。
- 残余图:解决流问题的一种辅助图,表示尚未加入到结果中的那些边及其剩余流量值。
- 增广路径:残余图中的一条可从头到尾的路径,存在时即可被添加到结果中。
表示方式
以下图为例

邻接表
| 顶点 | 邻接点 |
|---|---|
| 0 | {2,4,5} |
| 1 | {4,5} |
| 2 | {0,3,4} |
| 3 | {2} |
| 4 | {0,1,2,5} |
| 5 | {0,1,4} |
点集与边集
点集:{0,1,2,3,4,5}
边集:{(2,3),(0,2),(0,4),(0,5),(2,4),(1,4),(1,5),(4,5)}
当图为无向图时,边集中元素表示两个点之间有一条边;
当图为有向图时,边集中元素表示前者指向后者(或后者指向前者)
经典算法
拓扑排序
现实情况中存在着一系列事情中需要先完成某些事,然后才能做另一些事的限制。比如有时学习一门课程需要先学习其他课程、炒青椒肉丝需要先切肉等等;
这一系列事可以用一张有向图来表达,比如下图
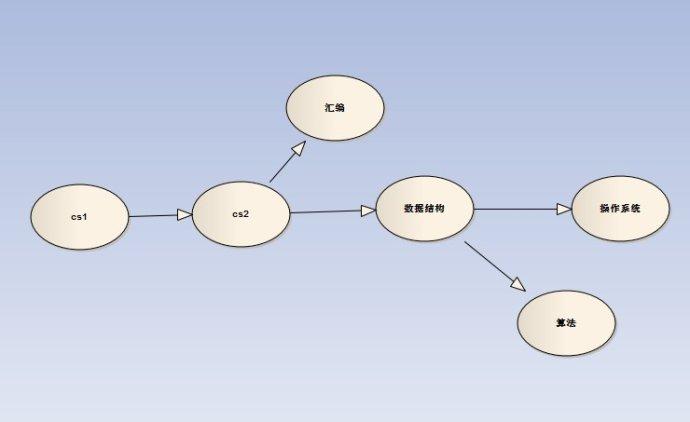
拓扑排序就是给出一个顶点序列,该序列满足:当存在(v->w)的边时,v需排在w的前面。
拓扑排序的正确结果并不唯一,只有满足上述条件即可。根据该条件可以看出,拓扑排序存在当且仅当图中无圈。
拓扑排序-图1 的一种结果可以是:cs1,cs2,数据结构,汇编,操作系统,算法
算法
解决拓扑排序问题的经典做法是为顶点增加一个入度的概念:指向点v的边数。
如果图是可以拓扑排序的,则必然存在入度为0的点(否则一定有环)。
算法步骤如下:
- 选取初始入度为0的点,推入队列中;
- 队列空吗?空则 7 ,不空则 3
- 从队列中取出点v,
- 将v添加到结果序列末尾
- 对于v的每一个下游点w,w的入度
,且当
=0时将
推入队列
- 回到2
- 对比结果序列的长度是否与点数一致,一致则排序成功,不一致则排序失败(存在圈)
最短路径
最短路径指给定一个图和一个起点,求起点到其他每个点的最短路径(有时只求长度,有时要给出路径上的点);
这里我们处理较简单的图,即没有负值边的图;
最短路径是广度优先搜索的典型应用。
无权图
无权图即每条边的权值都一样,此时路径长度等于边数。如下图所示
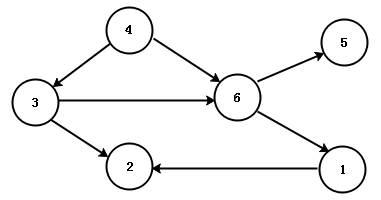
求最短路径问题的经典算法需要为点附加以下信息 :
- 唯一标识 i
- 是否已知 known
- 离给定起点的最短距离 d
- 上游点 p
算法步骤如下:
- 所有点的 d 设为
(起初所有点都视为离起点无穷远),known设为false , p设为null,
- 起点 s 的 d 设为 0;
- 将s推入队列
- 队列有数据吗,有进行5,无9
- 取出一个点 v
- v.known设为true
- 遍历v的邻接点w,如果
,则
,并将w推入队列
- 回到4
- 结束
如果要求的是起点s到指定终点e的最短路径,则可在遇到e并求得时结束。
有权图(Dijkstra算法)
有权图较之无权图稍复杂一些,主要是边的数量不再代表路径长度,边多的路径可能反而更短。
经典的解决方法是Dijkstra算法,这是一种贪婪算法。点的附加信息除无权图中4个,还需记录边的权值(v -> w 这条边的权值)
核心思想是每次搜索已知d且未处理的那些点中d最小的点,对其进行处理。
算法步骤
- 所有点的 d 设为
(起初所有点都视为离起点无穷远),known设为false , p设为null,
- 起点 s 的 d 设为 0;
- 是否还有未知的点,若有则做4,无则7
- 在未知的点中,取出d最小的点v
- v.known 设为 true
- 对v的所有邻接点w,若w未知且
,则
,
- 结束
第4步,取出最小d值点,这个的具体操作依据边的数量可以采用不同的数据结构,如果图是稠密的,则直接遍历列表效率较高;
而对于稀疏图,则可将点置于优先队列中,每次deleteMin取最小d值边。但引入一个问题,那就是
第6步更新v的邻接点w将比较麻烦,此时可以直接将更新过的w再插入优先队列,这又引入了可能重复处理的问题;
不过由于先后插入的两个w引用相同,故当最靠前的w弹出后,队列中的w全都将变成known的,于是可通过在deleteMin时过滤掉known的点来避免重复处理。
关键路径分析
关键路径分析是有向无圈图DAG的重要应用。可联系现实中的项目管理理解,从项目开始到结束,需要完成许多任务,有些任务之间有先后依赖,有些没有。无依赖的任务可以同时进行,有依赖的则后者必须等所有前置任务完成才能进行。
关键路径分析需回答的几个问题:
- 假设并行量无上限(人手充足),且每个任务均按规定时间要求完成,那么整体方案最早完成时间是何时?
- 哪些任务可以延迟而不使整个项目完成时间变长?可以延迟多久?
- 哪些任务延迟将项目整体完成时间延迟?(由无法延迟的任务组成的路径即关键路径)
对项目及下属任务的模拟,直观的抽象方式是使用动作节点图,如下图。

可以看出,若人手充足该项目最少耗时为10小时(A,C,F,H);
由此立即可以知道A,C,F,H的耗时一旦增加,整体项目完成耗时将增加,
而B单独增加2小时则不影响整体耗时。
若要用图论进行运算回答上述问题,最好是使用事件节点图。

事件节点图-1是完全的,即将每个动作都规定了起点和终点,这样比较直观且关系一定不会乱,但实际处理起来,多余的哑点和哑边将使算法效率降低,故可将其简化。
简化方式即去掉只由单个哑边进入的点,如“K开始”、“A开始”,而由两个及以上哑边进入的点则不能去掉,如“D开始”,“F开始”,有非哑边进入的点更不能去掉。

基于事件节点图的算法
1.计算事件节点的最早完成时间点。以 记录id为 i 的节点的最早完成时间,
记录从v事件到w事件的消耗时长。则可按以下公式计算各节点最早完成时间。
容易理解其含义,w的最早完成时间,取决于最晚到达它的那条路径。比如 “D开始” 的最早完成时间就是 max( 3+0 , 2+0)=3+0 ; 即取决于“A结束”到“D开始”这条路。
2.计算每个事件在不影响整体时间前提下的最晚完成时间点,以记录id为i的节点的最晚完成时间,
记录从v事件到w事件的消耗时长。则可按以下公式计算各节点最晚完成时间。
其含义这样理解,项目整体完成时间点减去本节点最晚完成时间点,就是剩余事件动作的时间,要给后续动作留足够时间,故取时间点最靠前的(即取min)
3.计算边的松弛时间,松弛时间即边代表的动作可独自延迟多久而不至于影响全局。








 本文介绍了图的基本概念,包括顶点、边和邻接关系,以及无向图和有向图的区别。重点讲解了拓扑排序的原理和应用,Dijkstra算法在无权和有权图中的最短路径求解,以及关键路径分析在DAG中的项目管理应用。通过实例和算法步骤详细阐述了这些核心概念和技术。
本文介绍了图的基本概念,包括顶点、边和邻接关系,以及无向图和有向图的区别。重点讲解了拓扑排序的原理和应用,Dijkstra算法在无权和有权图中的最短路径求解,以及关键路径分析在DAG中的项目管理应用。通过实例和算法步骤详细阐述了这些核心概念和技术。
















 7518
7518

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








