leetcode137:只出现一次的数字详解

原题连接：https://leetcode-cn.com/problems/single-number-ii/description/

一、题目说明

给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现了三次。找出那个只出现了一次的元素。

说明：

你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗？

示例 1:
   输入: [2,2,3,2]
   输出: 3
示例 2:
   输入: [0,1,0,1,0,1,99]
   输出: 99

二、思路解析

   学习评论区第一大佬的idea，采用状态机的方式解决这类问题。话不多说，开始推演。
1、首先这是一个N输入1输出的问题，我们将输入输出按照下图所示摆放：

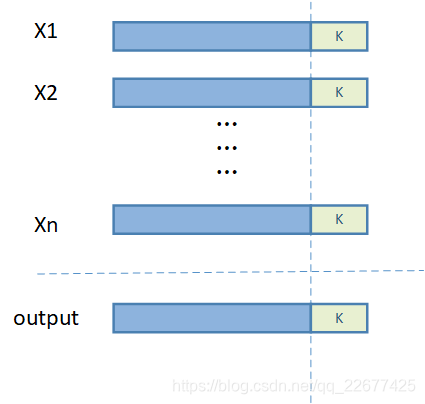
      输入输出都是int型，即长度为32bits，我们将其都分解为bit级。Output[k]受X[k]决定，是和X[k]有关的函数，假设这个函数是F（X[k]）。接下来我们就先讨论Output的第K位应该是0还是1，再由此延伸出如何计算Output整体。

3、函数F实现的功能其实也很简单，就是一个计数器的功能，如果出现一次1则加1，如果1的个数等于3则从0开始重新计数。那么为什么要这么做呢？因为按照题设，除了某个元素外所有的元素都会出现三次，那如果最后计数器的值是0就表明第K位为1的元素都出现了3次，所以这个特殊的元素的第K位就是0，即Output[K]的值等于0，相反Output[K]的值就是1。如果我们知道了Output每一位的值，我们也就得到了最终的结果啦。

三、状态机的概念

      上面提到的计数器实际上并不准确。因为计数器的值是从00—01—11—10—00，而我们的需求是 当1的个数等于3时从0开始重新计数，我们需要的状态改变是00—01—10—00（也可以是00—01—11—00或者其他的，只是用来区分三个状态）。因为状态有三种，所以我们需要2bits来表示，设低位为low，高位为high。接下来分别为low和high编写状态转换方程。
      状态方程的编写没有什么统一的模板，就是找规律啦，对于这道题来说，low是每有一个1则改变一次状态，但是！！！当high==1时是特例！所以low的方程如下
                  low = (low^X[k])&(~high);
（其中异或操作用来改变状态，~high用来应对特例）
      high的状态方程也差不多，相信你也可以动动手写出来了。这里就直接贴出来了(注意：这个high要写在low的后面)
                  high = (high^X[k])&(~low);

四、计算结果

     到这里我们也差不多搞定这道题了，因为Output的每一位执行的操作都是一样的，所以我们可以很直接的将low和high都扩展到32位。因此最终的代码如下：

int singleNumber(vector<int>& nums) {
    int low =0;int hi=0;
    for(int i=0;i<nums.size();i++)
    {
        low = (low^nums[i])&(~hi);
        hi = (hi^nums[i]) &(~low);
    }
    return low;
}