机器学习（一）— 决策树 & 随机森林

https://www.jianshu.com/p/907ab19751a8

https://blog.youkuaiyun.com/livan1234/article/details/80863222

决策树（Decision Tree）

决策树 通常包括三个步骤：特征选择、决策树的生成和决策树的修剪。

1、特征选择

2、决策树的生成

通过递归的选择最优特征，根据该特征对训练数据进行划分直到使得各个子数据集有一个最好的分类，最终生成特征树。

基于训练数据集生成决策树，生成的决策树要尽量大；

3、决策树的修剪

由于决策树的算法特性，为了防止模型过拟合，需要对已生成的决策树自下而上进行剪枝，将树变得更简单，提升模型的泛化能力。具体来说，就是去掉过于细分的叶节点，使其退回到父节点，甚至更高的节点，然后将父节点或更高的节点改为新的叶节点。如果数据集的特征较多，也可以在进行决策树学习之前，对数据集进行特征筛选。

用验证数据集对已生成的树进行剪枝并选择最优子树，这时损失函数最小作为剪枝的标准。

 

• 常用决策树算法

  决策树算法	算法描述
  ID3	其核心是在决策树的各级节点上，使用信息增益作为属性的选择标准，来帮助确定生成每个节点时所采用的合适属性。
  C4.5	C4.5决策树生成算法相对于ID3的重要改进是使用信息增益率来选择节点属性C4.5可以克服ID3的不足：ID3只使用于离散的描述属性，而从C4.5既可以处理离散的描述属性，也可以处理连续的描述
  CART	CART决策树是一种十分有效的非参数分类和回归方法，通过构建树、修剪树、评估树来构建一个二叉树。当终结点是连续变量时，该树为回归树；当终结点是分类变量，该树为分类树。

• 信息熵

在信息论中，熵是对不确定性的量度，在一条信息的熵越高则能传输越多的信息，反之，则意味着传输的信息越少。

熵越大，随机变量的不确定性就越大，

• ID3

  熵可以用来表示数据集的不确定性，熵越大，则数据集的不确定性越大。因此使用划分前后数据集熵的差值量度使用当前特征对于数据集进行划分的效果（类似于深度学习的代价函数）。

• C4.5

• CART

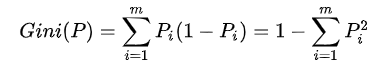
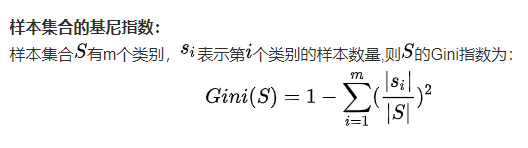
实例

  为了便于理解，利用以下数据集分别使用三种方法进行分类：

拥有房产	婚姻情况	年收入	能否偿还债务
是	单身	125	否
否	已婚	100	否
否	单身	70	否
是	已婚	120	否
否	离婚	95	是
否	已婚	60	否
是	离婚	220	否
否	单身	85	是
否	已婚	75	否
否	单身	90	是

  在进行具体分析之前，考虑到收入是数值类型，要使用决策树算法，需要先对该属性进行离散化。
  在机器学习算法中，一些分类算法（ID3、Apriori等）要求数据是分类属性形式，因此在处理分类问题时经常需要将一些连续属性变换为分类属性。一般来说，连续属性的离散化都是通过在数据集的值域内设定若干个离散的划分点，将值域划分为若干区间，然后用不同的符号或整数数值代表落在每个子区间中的数据值。所以，离散化最核心的两个问题是：如何确定分类数以及如何将连续属性映射到这些分类值。常用的离散化方法有等宽法，等频法以及一维聚类法等。

• 等宽离散化

 

• 据集如下：

拥有房产	婚姻情况	年收入	能否偿还债务
是	单身	中等收入	否
否	已婚	低收入	否
否	单身	低收入	否
是	已婚	中等收入	否
否	离婚	低收入	是
否	已婚	低收入	否
是	离婚	高收入	否
否	单身	低收入	是
否	已婚	低收入	否
否	单身	低收入	是

在实际使用时往往使用Pandas的cut()函数实现等宽离散化:

pd.cut(Income,3,labels=['低收入','中等收入','高收入'])

等宽法对于离群点比较敏感，倾向于不均匀地把属性值分布到各个区间，导致某些区间数据较多，某些区间数据很少，这显然不利用决策模型的建立。

 

• 等频率离散化

 等频法是将相同数量的属性取值放进每个区间，同样以收入数据的离散化为例：参考箱线图的分位点的概念，因为需要将收入属性的数值分为三个离散取值，需要选取四个分位点作为区间端点对数据进行划分，则每个分位点之间的分位点间隔为: 33.33\% 
相当于将一个长度为1的区间平均分为3个区间，于是得到四个分位点分别为：,

w = [1.0*i/3 for i in range(4)]
w = pd.Series(Income).describe(percentiles=w)[4:9]
# 以这几个分为点为区间端点将区间划分为三个子区间
w  = [w['0%'],w['33.3%'],w['66.7%'],w['100%']]
print(w)

# [60.0, 85.0, 100.0, 220.0]

对应收入属性的数据为：

拥有房产	婚姻情况	年收入	能否偿还债务
是	单身	高收入	否
否	已婚	中等收入	否
否	单身	低收入	否
是	已婚	高收入	否
否	离婚	中等收入	是
否	已婚	低收入	否
是	离婚	高收入	否
否	单身	低收入	是
否	已婚	低收入	否
否	单身	中等收入	是

 

 等频率离散化虽然避免了等宽离散化的数据分布不均匀的问题,却可能将相同的数据值分到不同的区间以满足每个区间具有相同数量的属性取值的要求。 

• 基于一维聚类的离散化
    基于一维聚类的离散化方法首先将连续属性的值用聚类算法进行聚类，然后再对聚类后得到的簇进行处理，将合并到一个簇的连续属性值做同一标记，聚类分析的离散化也需要用户指定簇的个数，从而决定产生的区间数。

 (0.0, 93.0] < (93.0, 165.0] < (165.0, 220.0]

• 计算对应特征选择准则

  在本次实例中选择使用基于聚类的离散化方法后得到的数据集进行指标计算。为了预测客户能否偿还债务，使用A（拥有房产）、B（婚姻情况）、C（年收入）等属性来进行数据集的划分最终构建决策树。

熵公式:采用CART 算法（也可采用ID3算法过程）

 

 

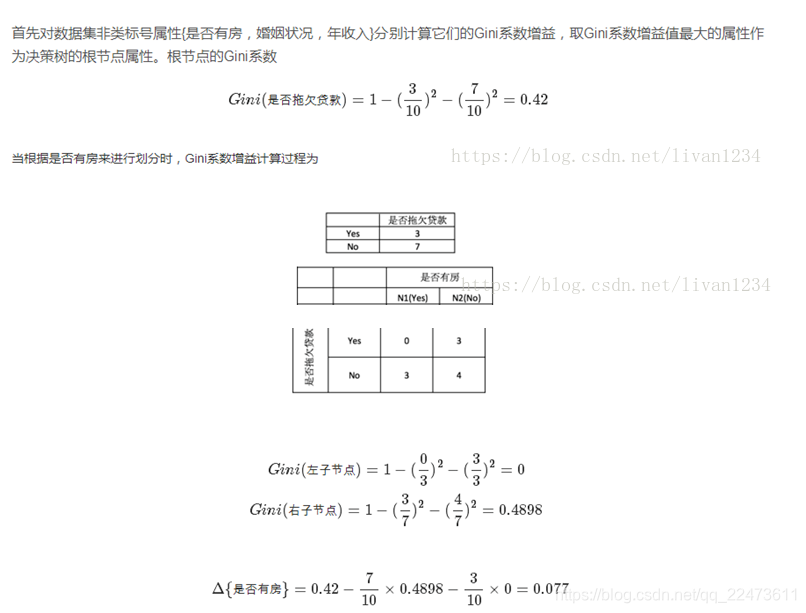
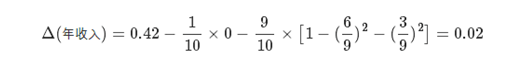
最后我们构建的CART如下图所示：

 

 

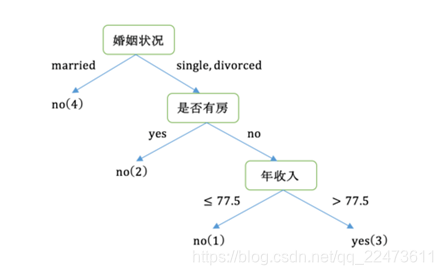
欠拟合：根本原因是特征维度过少，模型过于简单，导致拟合的函数无法满足训练集，误差较大； 
　　　　　　解决方法：增加特征维度，增加训练数据； 
过拟合：根本原因是特征维度过多，模型假设过于复杂，参数过多，训练数据过少，噪声过多，导致拟合的函数完美的预测训练集，但对新数据的测试集预测结果差。 过度的拟合了训练数据，而没有考虑到泛化能力。因为并不是树越高越好，因为树如果非常高的话，可能过拟合了。
　　　　　　解决方法：（1）减少特征维度；（2）正则化，降低参数值。

2、解决过拟合两种方法

剪枝

随机森林

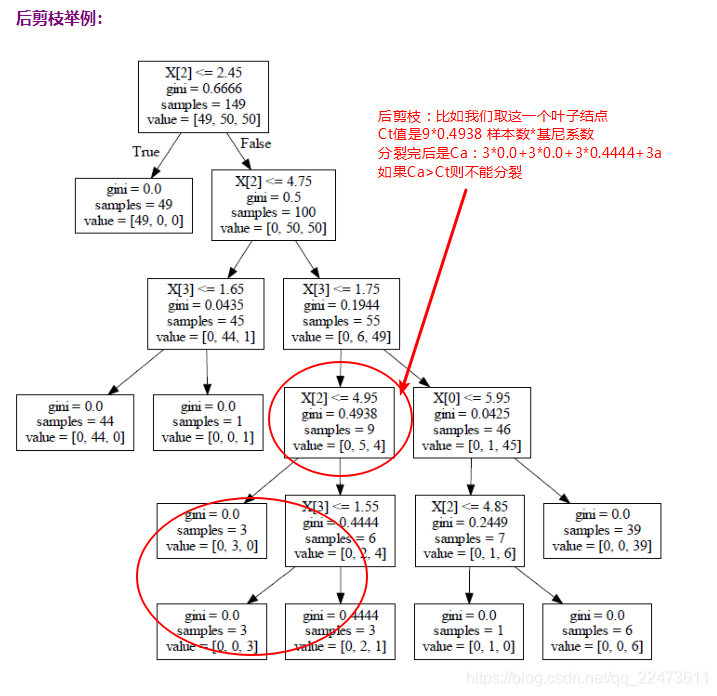
二、随机森林

 

Bagging思想的策略：

RandomForest(随机森林)是一种基于树模型的Bagging的优化版本，一棵树的生成肯定还是不如多棵树，因此就有了随机森林，解决决策树泛化能力弱的特点。(可以理解成三个臭皮匠顶过诸葛亮)

选取过程：

取某些特征的所有行作为每一个树的输入数据，采用放回抽样（bootstraping）得到训练数据，建立m棵CART决策树；这m个CART形成随机森林 ，每一个数中计算结果，少数服从多数，通过投票表决结果决定数据属于那一类。

  

随机森林之所以随机是因为两方面：样本随机+属性随机

 

随机森林的每一颗决策树之间是没有关联的。在得到森林之后，当有一个新的输入样本进入的时候，就让森林中的每一颗决策树分别进行判断，看看这个样本属于哪一类，然后看看哪一类被选择最多，则预测这个样本为那一类。一般来说，随机森林的判决性能优于决策树。