此主要讨论图像处理与分析。虽然计算机视觉部分的有些内容比如特 征提取等也可以归结到图像分析中来,但鉴于它们与计算机视觉的紧密联系,以 及它们的出处,没有把它们纳入到图像处理与分析中来。同样,这里面也有一些 也可以划归到计算机视觉中去。这都不重要,只要知道有这么个方法,能为自己 所用,或者从中得到灵感,这就够了。
8. Edge Detection
边缘检测也是图像处理中的一个基本任务。传统的边缘检测方法有基于梯度
算子,尤其是 Sobel 算子,以及经典的 Canny 边缘检测。到现在,Canny 边缘检 测及其思想仍在广泛使用。关于 Canny
算法的具体细节可以在 Sonka 的书以及 canny 自己的论文中找到,网上也可以搜到。最快最直接的方法就是看 OpenCV
的源代码,非常好懂。在边缘检测方面,Berkeley 的大牛 J Malik 和他的学生 在 2004 年的 PAMI
提出的方法效果非常好,当然也比较复杂。在复杂度要求不高 的情况下,还是值得一试的。MIT的Bill Freeman早期的代表作Steerable
Filter 在边缘检测方面效果也非常好,并且便于实现。这里给出了几篇比较好的文献,
包括一篇最新的综述。边缘检测是图像处理和计算机视觉中任何方向都无法逃避 的一个问题,这方面研究多深都不为过。
[1980] theory of edge detection
[1983 Canny Thesis] find edge
[1986 PAMI] A Computational Approach to Edge Detection
[1990 PAMI] Scale-space and edge detection using anisotropic diffusion
[1991 PAMI] The design and use of steerable filters
[1995 PR] Multiresolution edge detection techniques
[1996 TIP] Optimal edge detection in two-dimensional images
[1998 PAMI] Local Scale Control for Edge Detection and Blur Estimation
[2003 PAMI] Statistical edge detection_ learning and evaluating edge cues
[2004 IEEE] Edge Detection Revisited
[2004 PAMI] Design of steerable filters for feature detection using canny-like criteria
[2004 PAMI] Learning to Detect Natural Image Boundaries Using Local Brightness, Color, and Texture Cues
[2011 IVC] Edge and line oriented contour detection State of the art
翻译
可转向过滤器的设计和使用——http://tongtianta.site/upload
作者:William T. Freeman and Edward H. Adelson
摘要 -定向滤镜在许多早期视觉和图像处理任务中很有用。人们经常需要应用相同的滤波器,在自适应控制下旋转到不同的角度,或者希望计算不同方向的滤波器响应。我们提出了一种有效的体系结构,可以从基本滤波器的线性组合中合成任意方向的滤波器,从而允许将滤波器自适应地“引导”到任意方向,并根据方向解析地确定滤波器的输出。可控滤波器可以成对设计,以允许对相位和方向进行自适应控制。我们将展示如何设计和操纵滤镜,并展示其在多个任务中的使用示例:方向和相位分析,角度自适应滤镜,边缘检测和阴影形状。也可以构建自相似的可控金字塔表示。可以将相同的概念推广到3-D可控滤波器的设计,这在分析图像序列和体积数据时应该很有用。
索引词-早期视觉,边缘检测,滤波器设计,图像分析,方向分析,方向滤波器,阴影形状,纹理分析,小波。
Ⅰ 引言
定向滤镜用于许多视觉和图像处理任务,例如纹理分析,边缘检测,图像数据压缩,运动分析和图像增强。在许多这些任务中,在自适应控制和控制下应用任意定向的滤镜非常有用。检查作为方向和相位的函数的滤波器输出。我们将讨论允许以任意方向和相位合成滤波器的技术,并开发分析滤波器输出的方法。我们还将描述用于此类处理的高效架构,为二维和三维滤镜开发灵活的设计方法,并将滤镜应用于图像分析中的多个任务。这项工作的初步报告见[12]和[13]。
查找滤波器在许多方向上的响应的一种方法是应用同一滤波器的许多版本,每个版本在角度上的一些小旋转都彼此不同。一种更有效的方法是应用对应于几个角度的几个滤波器,并在响应之间进行内插。然后,需要知道需要多少个过滤器以及如何在响应之间正确地内插。使用正确的滤波器设置和正确的插值规则,就可以确定任意方向的滤波器的响应,而无需显式应用该滤波器。
我们使用“可控滤波器”一词来描述一类滤波器,其中任意方向的滤波器被合成为一组“基本滤波器”的线性组合。我们将显示二维和三维函数都是可控的以及控制一个给定滤波器需要多少个基本滤波器我们首先讨论二维情况。
Ⅱ 一个例子
作为介绍示例,请考虑用笛卡尔坐标x和y编写的二维圆对称高斯函数G:
为了方便起见,其中缩放比例和标准化常数已设置为1。定向导数算子是可操纵的,如众所周知的[8],[12],[16],[18],[21]-[24],[27],[34]。让我们将高斯在x方向上的n阶导数写为Gn。令(...)表示旋转算子,使得对于任何函数f(x,y), 都是f(x,y)绕原点旋转一个角度。高斯
都是f(x,y)绕原点旋转一个角度。高斯 的一阶x导数是
的一阶x导数是

旋转90°的相同功能是
这些功能如图1(a)和(b)所示。 显而易见,可以通过采用 和
和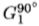 的线性组合来合成任意方向8的G1滤波器:
的线性组合来合成任意方向8的G1滤波器:
由于 和
和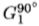 跨越了
跨越了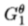 过滤器的集合,因此我们将它们称为
过滤器的集合,因此我们将它们称为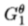 的基础过滤器。cos(
的基础过滤器。cos( )和sin(
)和sin( )项是这些基础过滤器的相应插值函数。
)项是这些基础过滤器的相应插值函数。
因为卷积是线性运算,所以我们可以通过对用 和
和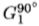 滤波的图像进行线性组合来合成以任意方向滤波的图像。
滤波的图像进行线性组合来合成以任意方向滤波的图像。
*代表卷积,如果

高斯滤波器的导数提供了可简化性的简单说明。 在下一部分中,我们将概括这些结果以涵盖各种各样的过滤器(有关此方法的最新扩展,请参见[36],[41])。

图1:可操纵文件的示例:(a)相对于高斯的x(水平)的 一阶导数; (b)
一阶导数; (b)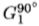 (即
(即 )旋转90°。 通过这两个滤波器的线性组合,可以创建
)旋转90°。 通过这两个滤波器的线性组合,可以创建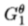 ,它是高斯一阶导数的任意旋转。 (c)
,它是高斯一阶导数的任意旋转。 (c) ,由
,由 形成。 用于从基本滤波器合成
形成。 用于从基本滤波器合成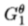 的相同线性组合也将从图像对基本滤波器的响应中合成图像对
的相同线性组合也将从图像对基本滤波器的响应中合成图像对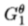 的响应。 (d)圆盘图像; (e)
的响应。 (d)圆盘图像; (e) (比上图小)盘旋(d);(f)
(比上图小)盘旋(d);(f)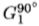 和(d)盘旋:(g)
和(d)盘旋:(g) 与(d)盘旋,得自 1/2(图(e)) +
与(d)盘旋,得自 1/2(图(e)) +  (图像(f))。
(图像(f))。
Ⅲ 二维转向定理
我们想要找到在什么条件下f(x,y)可以转向,即何时可以将其写成其旋转版本的线性和。
转向约束是
我们想知道什么函数f(x,y)可以满足(8),总和中需要多少项M,以及插值函数kj( )是什么。
)是什么。
我们将在极坐标 和
和 中工作。 令f 为可以在极角
中工作。 令f 为可以在极角 处以傅立叶级数展开的任何函数:
处以傅立叶级数展开的任何函数:
在附录A中,我们证明以下定理:
定理1:当且仅当插值函数k是解的解时,转向条件(8)才适用于以(9)形式扩展的函数

如果对于任何n,an(r)= 0,则应删除(10)左侧的对应的第(n)行和右侧的矩阵的第(n)行。
我们对控制特定函数f(r, )所需的最小数量的基础函数感兴趣。设T为正或负频率 -N≤n≤N 的数量,在极角傅里叶分解中,f(r,
)所需的最小数量的基础函数感兴趣。设T为正或负频率 -N≤n≤N 的数量,在极角傅里叶分解中,f(r, )具有非零系数 an(r)。例如,cos(
)具有非零系数 an(r)。例如,cos( )=
)= 的T = 2,而cos(
的T = 2,而cos( )+ 1 =
)+ 1 =  +e0 的T = 3。在附录B中,我们得出将引导 f(r,
+e0 的T = 3。在附录B中,我们得出将引导 f(r, )的任何形式的基本滤波器的最小数量,即以下等式成立:
)的任何形式的基本滤波器的最小数量,即以下等式成立:
其中gj(r, )可以是任何函数集。定理2给出结果。
)可以是任何函数集。定理2给出结果。
定理2:令T为可扩展为(9)形式的函数f(r, )的非零系数an(r)的数量。然后,足以使f(r,
)的非零系数an(r)的数量。然后,足以使f(r, )转向(11)的基函数的最小数量为T,即(11)中的M必须> = T。
)转向(11)的基函数的最小数量为T,即(11)中的M必须> = T。
使用函数本身的旋转形式作为基础函数,如(8)中的T基本函数方向;必须选择以使(10)中矩阵的列线性独立。在实践中,出于对称性和对噪声的鲁棒性的原因,我们选择在0和Π 之间夹角相等的基函数。注意,插值函数kj( )不依赖于滤波器f(r,
)不依赖于滤波器f(r, )的傅立叶角分解中的非零系数an(r)的值。
)的傅立叶角分解中的非零系数an(r)的值。
一维带限函数可以由与傅立叶项数(即自由度数)相对应的有限数量的样本表示。定理1和2表明,角度带限函数的行为相同。
我们通过重新推导Gi的转向方程来说明定理1的使用。在极坐标中,高斯的第一个导数是
由于 (r,
(r, )在极角
)在极角 的傅里叶分解中具有两个非零系数,因此根据定理1,两个基函数足以合成
的傅里叶分解中具有两个非零系数,因此根据定理1,两个基函数足以合成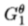 。插值函数可从(10)中找到,除第二行外的所有条目均被删除:
。插值函数可从(10)中找到,除第二行外的所有条目均被删除:
如果我们选择一个基函数定向为 1 = 0°,另一个基函数定向为
1 = 0°,另一个基函数定向为 2 = 90°,则(13)给出k1(
2 = 90°,则(13)给出k1( )= cos(
)= cos( )和k2(
)和k2( )= sin(
)= sin( )。因此,定理I告诉我们
)。因此,定理I告诉我们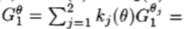
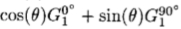 与(4)一致。
与(4)一致。
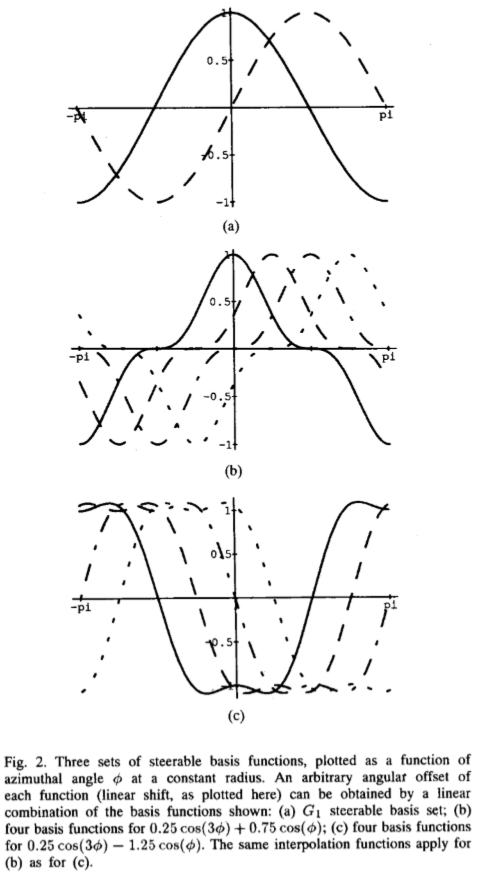
图2:三组可操纵的基础函数,它们是在恒定半径下作为方位角 的函数绘制的。 可以通过所示基础函数的线性组合来获得每个函数的任意角度偏移(线性偏移,如此处所示):(a)G1可转向基础集; (b)0.25cos(3
的函数绘制的。 可以通过所示基础函数的线性组合来获得每个函数的任意角度偏移(线性偏移,如此处所示):(a)G1可转向基础集; (b)0.25cos(3 )+ 0.75cos(
)+ 0.75cos( )的四个基函数;(c)0.25 cos(3
)的四个基函数;(c)0.25 cos(3 )-1.25cos(
)-1.25cos( )的四个基函数。 与(c)相同的插补函数适用于(b)。
)的四个基函数。 与(c)相同的插补函数适用于(b)。
图2显示了一些可控基本滤波器的1-D截面,它们是在恒定半径处作为角度 的函数绘制的。任何一条曲线的任意平移都可以写成曲线图上所示基础曲线的线性组合(滤波器的旋转对应于这些曲线图上的平移)。图2(a)显示了以恒定半径绘制的
的函数绘制的。任何一条曲线的任意平移都可以写成曲线图上所示基础曲线的线性组合(滤波器的旋转对应于这些曲线图上的平移)。图2(a)显示了以恒定半径绘制的 和
和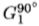 的一维切片的正弦变化。在这种情况下,操纵特性是对以下事实的重新陈述:两个正弦曲线的线性组合可以合成任意相位的正弦曲线。图2(b)和(c)是分别具有0.25cos(3
的一维切片的正弦变化。在这种情况下,操纵特性是对以下事实的重新陈述:两个正弦曲线的线性组合可以合成任意相位的正弦曲线。图2(b)和(c)是分别具有0.25cos(3 )+ 0.75cos(
)+ 0.75cos( )和0.25 cos(3
)和0.25 cos(3 )-1.25cos(
)-1.25cos( )的方位角分布的函数的可操纵基础集的1-D截面。由于每个函数在两个频率上都具有非零傅立叶系数,根据定理1,四个基函数足以满足转向要求,因为两个函数都包含相同频率(即使幅度不同)的正弦曲线,所以它们使用相同的kj(
)的方位角分布的函数的可操纵基础集的1-D截面。由于每个函数在两个频率上都具有非零傅立叶系数,根据定理1,四个基函数足以满足转向要求,因为两个函数都包含相同频率(即使幅度不同)的正弦曲线,所以它们使用相同的kj( )插值系数。
)插值系数。
对于用笛卡尔坐标x和y [12]表示为多项式的函数,有一个定理1的版本很方便。在附录C中,我们证明以下定理:
定理3:令f(x,y)= W(r)PN(r,y),其中W(r)是任意窗口函数,PN(x,y)是x和y中的N阶多项式,其系数可能取决于r。 2N + 1个基函数的线性组合足以合成旋转到任意角度的f(x,y)= W(r)PN(x,y)。等式(10)给出了插值函数kj( )。如果PN(x,y)仅包含偶数[奇数]阶项(n + m偶数[奇数]的项xnym),则N + 1个基函数就足够了,并且(10)可以修改为仅包含偶数左侧列向量和右侧矩阵的[奇数]行(从零开始计数)。
)。如果PN(x,y)仅包含偶数[奇数]阶项(n + m偶数[奇数]的项xnym),则N + 1个基函数就足够了,并且(10)可以修改为仅包含偶数左侧列向量和右侧矩阵的[奇数]行(从零开始计数)。
定理3允许通过将所需滤波器与多项式乘以旋转对称窗函数进行拟合来设计可控滤波器,这比在极坐标中使用傅立叶级数要简单。但是,定理3不能保证找到可以操纵滤波器的最小基函数数。用傅立叶级数表示该函数可以明确说明操纵该函数所需的最小基本滤波器数。在多项式表示中,多项式阶数仅表示足以进行转向的多个基函数。例如,将以极坐标表示形式编写的角对称函数x2 + y2视为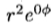 。定理2表示仅需一个基函数即可对其进行转向;仅使用多项式阶数的定理3仅表示足以进行转向的基函数为2 + 1 = 3。
。定理2表示仅需一个基函数即可对其进行转向;仅使用多项式阶数的定理3仅表示足以进行转向的基函数为2 + 1 = 3。
以上定理表明,可操纵性是多种函数的属性,即,所有函数都可以表示为角度的傅立叶级数,或者表示为径向对称窗口函数的x和y的多项式展开。由于每个高斯导数都是一个多项式(Hermite多项式[32])乘以一个径向对称的窗函数,因此它们是可导的。
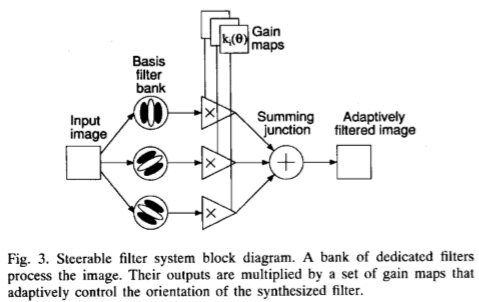
图3:可调滤波器系统框图。 一排专用滤镜可处理图像。 它们的输出乘以一组增益图,这些增益图可自适应地控制合成滤波器的方向。
图3显示了使用可控滤波器的一般体系结构(参见Koenderink和van Doorn [22]-[24],他们将这种体系结构与高斯派生算法结合使用;以及Knutsson等人,[21],将其与相关滤波器一起使用)。前端由一堆永久性的专用基础滤波器组成,这些滤波器始终对图像进行卷积处理。它们的输出乘以一组增益掩码,在每个位置和时间应用适当的插值函数。最终求和产生自适应滤波的图像。
本文介绍的可控滤波器的另一种方法是将函数的所有旋转投影到正交基函数的完整集合上,例如Hermite函数或刻面模型中使用的多项式[16]。然后可以通过更改膨胀系数来过滤过滤器。这种扩展允许对文件管理器进行灵活控制,但是出于转向的目的,它们通常需要比定理2给出的最小数量更多的基本函数。例如,2N + 1个基本函数足以操纵任何N阶多项式,而完整的集合2-D多项式基函数的个数将需要(N + 1)(N + 2)/ 2个基函数(对于每个阶数0<=N,n + 1个基函数)。此外,一般分解可能需要额外的基本函数,以适合该函数的旋转对称组件,当使用函数的旋转形式本身作为基本函数时,不需要额外的基本函数来进行操纵。
IV 设计转向过滤器
给定基础过滤器,所有在角频率上有带宽限制的函数都是可操纵的。然而,实际上,最有用的功能是那些需要少量基本过滤器的功能。
例如,我们将基于高斯G2的二阶导数的频率响应设计可控正交对。如果一对滤波器具有相同的频率响应,但相位相差90°(即彼此是希尔伯特互斥体,则是正交的(4)),这种滤波器对可以独立于相位分析频谱强度,并允许合成具有任意相位的频率响应的滤波器,它们在运动,纹理和方向分析中都有应用[1],[3],[11],[17],[19],[31],[38]。高斯导数对于图像分析是有用的功能[22]-[24],[45],并且它们的可控正交对对许多视觉任务将很有用。
首先,我们为高斯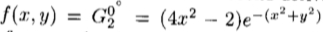 的二阶导数设计一个可操纵的基础集。这是二阶偶数奇偶多项式和一个径向对称的高斯窗的乘积;因此,根据定理3,三个基函数就足够了。公式(10)对于插值函数kj(
的二阶导数设计一个可操纵的基础集。这是二阶偶数奇偶多项式和一个径向对称的高斯窗的乘积;因此,根据定理3,三个基函数就足够了。公式(10)对于插值函数kj( )变为
)变为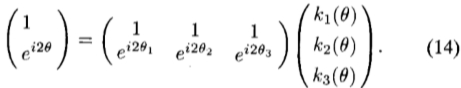
要求(14)的实部和虚部都一致,就可以得到一个由三个方程组成的系统。使用 1 = 0°,
1 = 0°, 2 = 60°和
2 = 60°和 3 = 120°求解系统,得出
3 = 120°求解系统,得出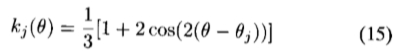
我们有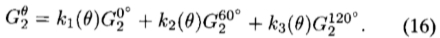
通过找到与多项式乘以高斯的最小平方,可以形成G2的希尔伯特变换的近似值。我们使用三阶奇偶校验多项式找到了令人满意的近似值(总误差功率为总信号功率的1%),该多项式可以通过四个基函数进行控制,我们将此近似值称为H2。附录F中其他几个多项式的阶数
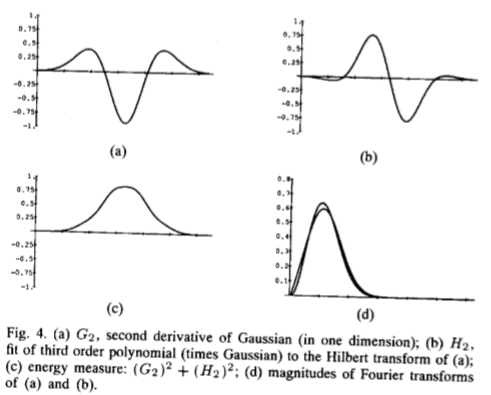
图4.(a)G2,高斯二阶导数(在一维中); (b)H2。 三阶多项式(乘高斯)对(a)的希尔伯特反演的拟合; (c)能量测量:(G2)2+(H2)2; (d)(a)和(b)的傅立叶变换的宏。
图4(a)和(b)显示了G2和H2的一维切片。 H2对G2的希尔伯特变换的拟合质量相当好,如图4(c)所示的光滑的,类似高斯的能量函数(G2)2+(H2)2以及每个函数的傅立叶光谱,如图4(d)所示。
G2和H2的七个基本函数足以在相位和方向上任意移动G2。图5中显示了这七个基函数及其傅里叶变换的幅度。表I和II列出了基于高斯导数及其希尔伯特变换的几阶导数的其他正交对。
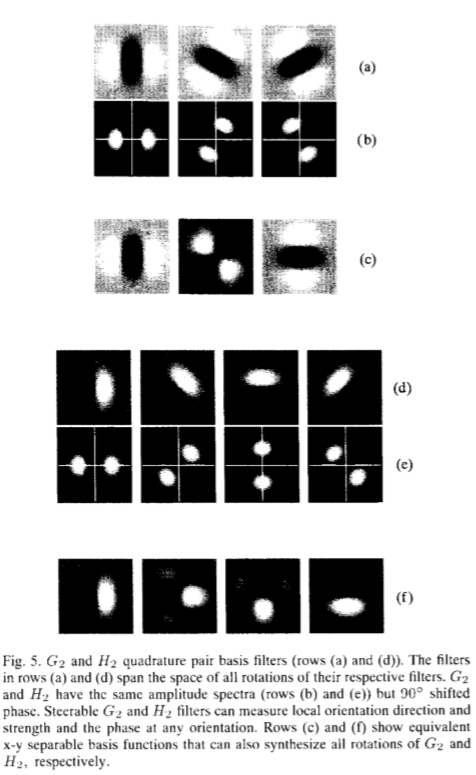
图5:G2和H2正交对基滤波器(行(a)和(d)。行(a)和(d)中的滤波器跨越其各自滤波器的所有旋转空间)G2和H2具有相同的幅度 光谱(行(b)和(e)),但相移90°。可操纵的G2和H2滤波器可以测量局部取向方向和强度以及任意取向的相位;行(c)和(f)显示了等效的xy可分离基函数 也可以分别合成G2和H2的所有旋转。
A.设计可分离的导向接头
对于大多数可操纵的过滤器而言,基本过滤器并非都是x-y可分离的,这会带来很高的计算成本。对于机器视觉应用,我们只希望有x-y个可分离的基函数。
我们首先注意到,对于所有可以在x和y中以多项式形式编写的函数f,都有x-y可分离的基础,尽管它可能有许多基础函数。将旋转公式应用于多项式的每个x和y项,将得出x和y的幂的乘积之和,其系数是旋转角度的函数: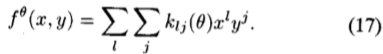
旋转多项式中的每个x和y乘积可以认为是x-y可分离的基函数,其系数klj( )是插值函数。
)是插值函数。
但是,在许多情况下,存在一个x-y可分离的基集,该基集仅包含最少数量的基本滤波器,但跨越了感兴趣功能的所有旋转空间。这样的可分离基础允许以高计算效率来应用可转向滤波器。图5的(c)和(f)行显示了G2和H2滤波器的x-y可分离基集。表Ⅲ,Ⅴ,Ⅶ和Ⅸ 给出了G2,H2,G4和H4基本滤波器的x-y可分离版本的功能形式和数字滤波器值。在附录D中,我们导出了这些x-y可分离函数的控制公式,并显示了如何找到可分离基函数。
B 离散空间过滤器
转向定理是针对连续函数得出的,可能有人担心,当一个函数使用离散采样函数时会出现新的困难。但是,如果连续函数是可操纵的,则它的采样版本可以以完全相同的方式操纵,因为空间采样和操纵的顺序是可互换的。一组空间采样基函数的加权和等于连续基函数加权和的空间采样。因此,通过简单地对连续滤波器进行采样就可以获得数字可控滤波器。表Ⅲ,Ⅴ,Ⅶ和Ⅸ中给出了G2,H2,G4和H4的空间采样版本。
滤波器也可以在频域中设计,其中可以将设计的径向部分和角度部分分开[19]。传统的滤波器设计技术[25],[33]允许设计具有所需径向响应的圆形对称二维滤波器。然后,可以在该滤波器上施加必要的角度变化,以通过频率采样[25]设置可控制的基准(如果角度响应相对平滑)。对频率采样响应进行反变换,得到滤波器内核。
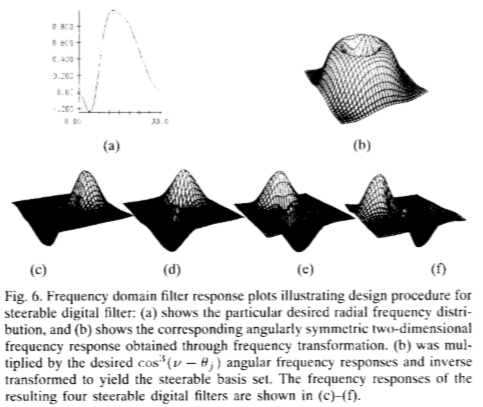
图6:频域滤波器响应图说明了可控数字滤波器的设计过程:(a)显示了特定的所需径向频率分布,(b)显示了通过频率变换获得的相应的角对称二维频率响应。 (b)乘以所需的cos3(v- j)角频率响应,然后逆变换以得出可操纵的基集。 (c)-(f)中显示了所得的四个可控数字滤波器的频率响应。
j)角频率响应,然后逆变换以得出可操纵的基集。 (c)-(f)中显示了所得的四个可控数字滤波器的频率响应。
图6显示了一个示例。滤波器被设计为可转向的,自反转金字塔图像分解的一部分[41],下面将对此进行描述。多尺度分解的约束导致径向频率响应如图6(a)所示。我们使用频率变换方法[25]将一维滤波器转换为几乎成角度对称的二维滤波器(见图6(b))。
选择了径向频带之后,我们接下来通过施加cos3(v)的角度变化将频带分为四个定向子频带,其中y是频率的方位角。该函数具有四个角频率(±3和±1),因此,根据定理1,需要四个基本函数来进行转向。我们对径向对称核进行傅立叶变换,再乘以四个所需的cos3(v- j)角响应,然后进行逆变换以获得基本滤波器脉冲响应。图6(c)-(f)显示了所得数字可控滤波器的频率幅度响应。
j)角响应,然后进行逆变换以获得基本滤波器脉冲响应。图6(c)-(f)显示了所得数字可控滤波器的频率幅度响应。
C.用于多尺度分解的可控金字塔
我们已经使用了可控滤波器来形成多尺度自反转金字塔分解[41]。将分解的每个滤波器一次应用于信号给出变换系数;第二次应用每个滤波器(滤波器抽头值反映在原点附近),并将结果相加即可重建图像的低通版本。由于金字塔的所有滤波器都是带通的,因此必须重新添加高通残留图像以重建原始图像(与[43]一样)。为了实现这种分解,我们设计了极性可分离设计的角度和径向分量,以使每个滤波器的响应平方在频率平面上相加。
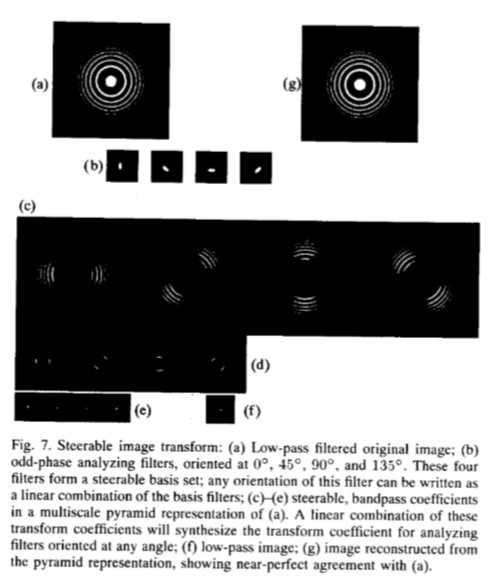
图7:可转换的图像变换:(a)低通滤波后的原始图像; (b)分别位于0°,45°,90°和135的奇相分析滤波器。这四个滤波器构成了可操纵的基集;该滤波器的任何方向都可以写成基滤波器的线性组合; (c)-(e)(a)的多尺度金字塔表示中的可控带通系数。 这些变换系数的线性组合将合成变换系数,以分析以任何角度定向的滤波器。 (f)低通图像; (g)从金字塔表示重建的图像,显示与(a)接近完美的一致性。
图7显示了可操纵的金字塔表示。在金字塔的每个级别上的四个带通滤波器形成一个可操纵的基础集。金字塔基础滤波器的方向为0°,45°,90°,135°,但是可以从四个基础滤波器输出的线性组合中找到任何滤波器方向的系数。当在每个级别再次应用基本滤镜时,金字塔会以接近完美的一致性折叠回原始图像的滤镜版本。可操纵的金字塔图像变换允许在所有范围内控制方向分析。
可控金字塔是一种图像变换,其所有基本函数都是通过单个函数的扩张,平移和旋转来得出的;它与其他分解(例如小波变换[15],[26]和皮质变换[43])具有某些属性。关于自相似图像分解的大多数工作都涉及离散正交函数,例如正交镜像滤波器(QMF)和小波[10],[26],[40],[42]。对于图像编码应用[2],[26],[44],这样的金字塔可能非常有效。这些表示通常是在矩形网格上使用x-y可分离的滤波器构建的,这大大限制了可以实现的方向调整的质量。 Simoncelli和他的同事[2],[39]已经基于放置在六边形格子上的滤波器设计了QMF金字塔;除了正交和自相似之外,这些金字塔在所有波段上都具有良好的方向调整。但是,基本函数不可操纵,因此,该表示对于方向分析不是最佳的。 [9],[14],[28],[43]描述了具有方向调整的非正交金字塔。
与基于QMF的金字塔不同,此处描述的可操纵金字塔明显过剩。如果不计算残差图像,则表示中的系数是原始图像的5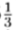 倍(与Laplacian金字塔[5]相比,过完整度是1
倍(与Laplacian金字塔[5]相比,过完整度是1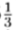 倍,但对于四个方向中的每个方向)。过高的完整性会限制其效率,但会增加其在许多图像处理任务中的便利性。尽管它不是正交的,但仍然是自反转的,这意味着用于构建金字塔表示的滤镜与用于重建的滤镜相同。
倍,但对于四个方向中的每个方向)。过高的完整性会限制其效率,但会增加其在许多图像处理任务中的便利性。尽管它不是正交的,但仍然是自反转的,这意味着用于构建金字塔表示的滤镜与用于重建的滤镜相同。
Ⅴ 应用
转向过滤器对于早期视觉中的许多任务很有用。我们在下面介绍了四个应用程序-方向和相位分析,角度自适应滤波,边缘检测和阴影形状。
A.分析当地取向
方向分析是早期视觉的重要任务[18],[19],[21],[46]。 Knutsson和Granlund [19]设计了一种优雅的方法,用于组合正交对的输出以提取方向量度。我们描述了一种相关方法,该方法可以最佳利用第四节中设计的过滤器。我们通过转向角为 的正交带通滤波器对的平方输出来测量沿特定方向的定向强度。我们将此频谱功率称为“定向能量” E(
的正交带通滤波器对的平方输出来测量沿特定方向的定向强度。我们将此频谱功率称为“定向能量” E( )。
)。
使用高斯的n阶导数及其希尔伯特变换作为带通滤波器,我们得到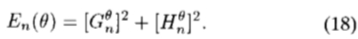
写 作为基本滤波器的总和输出时间插值函数,(18)简化为角度的傅立叶级数,其中由于平方运算,仅出现偶数频率:
作为基本滤波器的总和输出时间插值函数,(18)简化为角度的傅立叶级数,其中由于平方运算,仅出现偶数频率: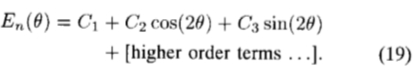
我们使用最低频率项来近似主导方向(使En( )最大化的方向)的方向
)最大化的方向)的方向 d和强度S
d和强度S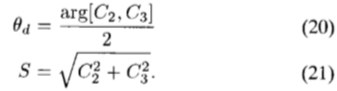
如果本地仅存在一个方向,则此近似值是精确的。

图8:(a)爱因斯坦的原始图像; (b)(a)的定向图,该定向图使用傅立叶级数展开中的最低阶项针对由G2和H2测得的定向能量制成。表ⅩⅠ给出了这些术语的公式。
图8(b)显示了使用此方法导出的方向图,使用G2和H2来测量E2( )。线长与S成正比,S是沿该方向的对比度。测得的方向和强度可准确反映输入图像的方向结构。定向角的测量直接从基本滤波器的输出进行,而无需实际执行转向操作。表XI列出了C2和C3作为x-y可分离G2和H2基本滤波器输出的基本滤波器输出的函数。
)。线长与S成正比,S是沿该方向的对比度。测得的方向和强度可准确反映输入图像的方向结构。定向角的测量直接从基本滤波器的输出进行,而无需实际执行转向操作。表XI列出了C2和C3作为x-y可分离G2和H2基本滤波器输出的基本滤波器输出的函数。
1)多个方向:在包含角和透明或重叠对象的区域中,在给定位置可能存在多个方向。诸如G2之类的滤镜由于其有限的角度分辨率而无法发出信号指示某个点上存在两个方向。为了对方位进行更高分辨率的分析,可以使用具有较窄频率调谐的可控滤波器,例如高斯G4的四阶导数。这种方法允许在单个点分析多个定向结构。
附录G中给出了可控正交滤波器对G4 和 H4的滤波器抽头和分析形式。(H4是5阶多项式乘以高斯到G4的希尔伯特变换的最小二乘拟合)。
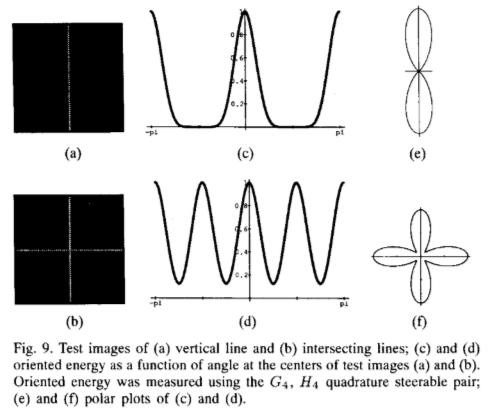
图9:(a)垂直线和(b)相交线的测试图像; (c)和(d)定向能量与测试图像(a)和(b)中心的角度成函数关系。 定向能量是使用G4,H4正交可控对测量的。 (e)和(f)(c)和(d)的极坐标图。
图9显示了两个测试图像(一条垂直线和一条十字线)以及它们的定向能量与角度的关系,它们在中心使用G4,H4正交对在直角坐标和极坐标中进行了测量。请注意,从小花形状可以看出,可操纵的过滤器足以描述十字的多个方向。
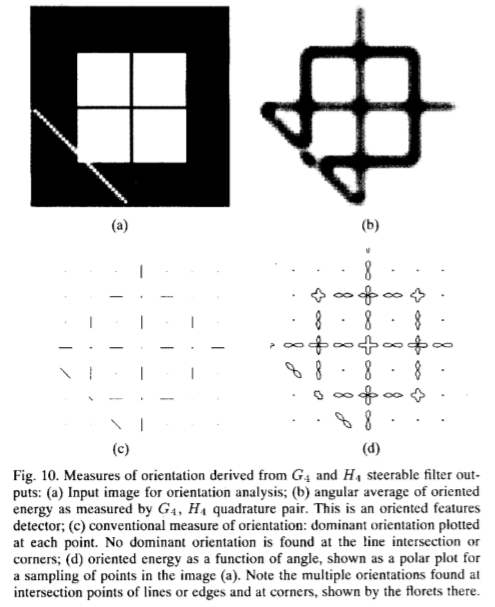
图10:从G4和H4得出的方向测量值,可操纵的滤波器输出:(a)用于方向分析的输入图像; (b)用G4,H4正交对测量的定向能的角均值。 这是一个定向特征检测器;(c)常规的定向度量:在每个点上绘制的主导方向。 在直线相交处或拐角处未发现主导方向;(d)定向能量随角度变化,显示为图像中点采样的极坐标图(a)。 注意在直线或边线的交点和拐角处发现的多个方向,如那里的小花所示。
图10显示了使用G4,H4正交对的测试图像(a)及其定向能量的几种度量。图10(b)显示了定向能量的dc分量,它是(18)的角平均值,因为我们使用的是正交对,所以该能量量度同时响应线和边。取向,根据(18)的最低阶傅立叶项计算,每个点仅允许一个取向,在取向结构的相交处未检测到主导取向。图10(d)显示了各点取向能量分布的极坐标图请注意,此度量捕获了相交和拐角处存在的多个方向,如小花所示。
可以通过为观察到的每个方向构造一个不同的正交对来计算这些量度。但是,使用可控滤波器大大降低了计算量。

图11:(a)纹理图像; (b)每四个像素(a)的定向能量的极坐标图。 每幅图均通过定向能量所有角度上的平均值进行归一化;(c)(a)的细节(缩放和模糊); (d)归一化极坐标图,显示每个像素的(c)取向能量。
图11显示了纹理的细节,并且纹理图像中每个像素处都有相应的极性方向图,从而提供了纹理细节的丰富描述。注意,一个优势方向的小花与另一优势方向的小花被同时存在两个方向的小花隔开。
B.角度自适应滤波
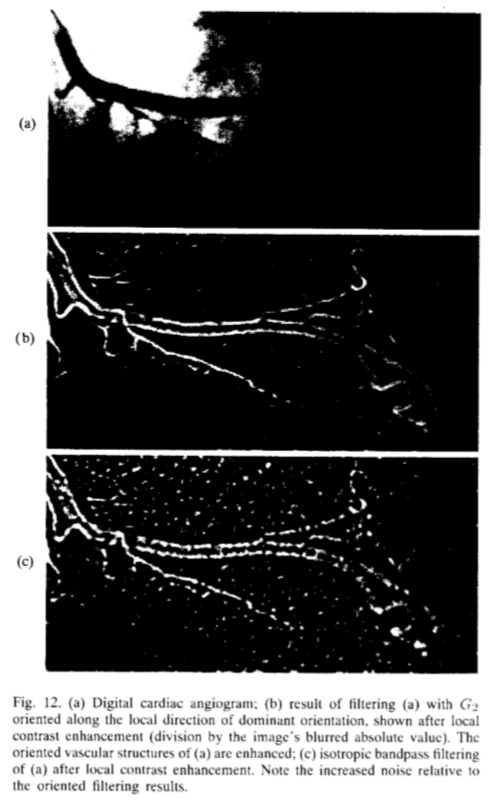
图12:(a)心脏数字血管造影:(b)过滤结果(a)G2沿显性方向的局部方向取向,在局部对比度增强后除以图像(绝对值模糊)。 (a)的定向血管结构得到增强;(c)(a)局部对比增强后各向同性带通滤波。 请注意,相对于定向滤波结果,噪声增加了。
可以通过角度自适应滤波[18],[21],[27]去除噪声并增强定向结构。可操纵的过滤器为这种处理提供了一种有效的方法。图12(a)示出了数字心脏血管造影。从G2和H2基本滤波器的输出,我们发现图像中每个点的主导方向,如第V-A节所述。 (为了抑制噪声,我们在空间上模糊了(21)中使用的傅立叶系数C2和C3)。
然后,我们采用由(15)和(16)给出的G2基本滤波器输出的适当组合,以沿主导方向的局部方向自适应地操纵G2。此步骤不需要其他过滤。为了增强局部对比度,我们将滤波后的图像除以其绝对值的局部平均值。结果(见图12(b))突出显示了血管造影的定向血管结构。找到主导方向,沿其引导G2并得出增强图像的整个过程仅涉及图像通过基本滤波器的一次通过。结果与相同频率通带的各向同性滤波器的输出相比,噪声要小得多(请参见图12(c),以相同的方式增强对比度)。
C.轮廓检测
具有方向调整功能的滤波器通常用于检测线条和边缘[6],[16]。一种广受欢迎的特征检测器是Canny的边缘算子[6],该算子经过优化可检测台阶边缘。 Canny的系统还可以与不同的滤镜选择一起使用,以检测台阶边缘以外的特征。
当与边缘配合使用时,经过优化以与边缘配合使用的滤镜将产生虚假响应。例如,当Canny边缘滤镜应用于一条线而不是一条边缘时,它将在其输出中产生两个极值而不是一个极值,并且每个极值都移到实际线位置的一侧。另一方面,如果为检测线而优化了一个滤波器,它将给出边缘的虚假响应。由于自然图像包含线条,边缘和其他轮廓的混合,因此通常希望找到一种对各种轮廓类型做出适当响应的轮廓检测器。线性滤波器不能完成此任务,但是从正交对得出的局部能量度量可以很好地完成任务。 Morrone等人[30],[31]已经表明,局部能量测量在恒定相位的点处给出峰值响应,该响应是空间频率的函数,并且它们对应于人类观察者将轮廓定位的点。 Perona和Malik [37]表明,对于各种边缘类型,能量测量是最佳的。我们已经描述了使用正交对可控滤波器对局部能量量度的提取。现在,我们希望使用可控的能量度量来生成稀疏的图像描述,并将结果与诸如Canny's这样的系统的结果进行比较。
在进行比较时,我们必须牢记Canny的完整方案涉及三个阶段:过滤阶段,初始决策阶段以及清理候选边缘的复杂后处理阶段。过滤器只是大量后处理设备的前端。因此,为了进行比较,我们删除了Canny的滤波阶段,并替换了可控能源度量的输出;我们保留了后处理阶段的完整性。
我们从麻省理工学院人工智能实验室获得了Canny边缘检测器的Lisp代码。
对于轮廓检测器,我们使用G2和H2正交可控基集。我们首先在每一个位置找到主导方向的角度 d,乘以可转向正交对的最大响应角度,如第V-A节所述。然后,我们找到在主导方向上随处可见的正交对滤波器响应的平方幅度:
d,乘以可转向正交对的最大响应角度,如第V-A节所述。然后,我们找到在主导方向上随处可见的正交对滤波器响应的平方幅度: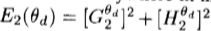 。如果E2(
。如果E2( d)在垂直于局部方向
d)在垂直于局部方向 d的方向上处于局部最大值,则给定点(x0,y0)是潜在的轮廓点。然后,像Canny方法一样,使用E2(
d的方向上处于局部最大值,则给定点(x0,y0)是潜在的轮廓点。然后,像Canny方法一样,使用E2( d)的值作为阈值的基础而不是梯度幅度,使用磁滞对局部最大值点进行阈值化。
d)的值作为阈值的基础而不是梯度幅度,使用磁滞对局部最大值点进行阈值化。
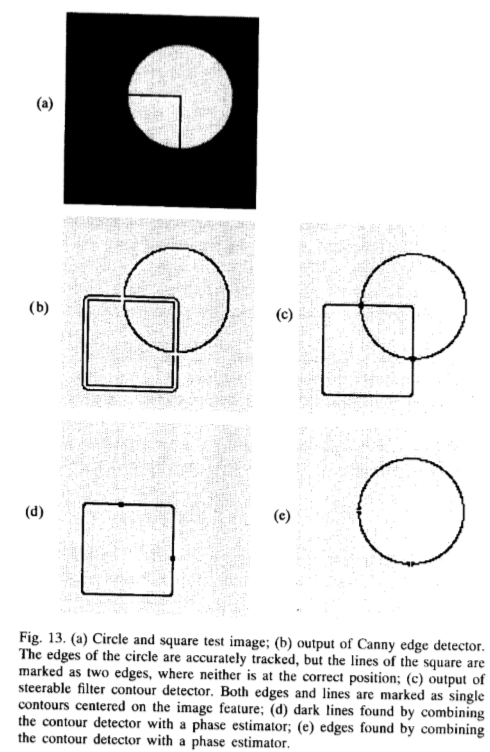
图13:(a)圆形和方形测试图像; (b)Canmy边缘检测器的输出。 圆的边缘被精确地跟踪,但是正方形的线被标记为两个边缘,两个边缘都不在正确的位置。 (c)转向滤波器轮廓检测器的输出。 边缘和线条都标记为以图像特征为中心的单个轮廓。 (d)通过组合轮廓检测器和相位估计器而发现的暗线; (e)通过结合轮廓检测器和相位估计器发现的边缘。
图13(a)显示了一个由实心圆和空心正方形组成的测试图像。 Canny边缘检测器的响应如图13(b)所示。它正确地找到了圆的边缘,但发出信号在定义正方形的线的两侧上出现双边缘。图13(c)显示了使用可控正交对的输出。新的检测器以正确地以圆形和正方形为中心的单个值进行响应,从而对相同信息进行了更清晰,更稀疏的描述。
因为G2和H2的响应指示局部相位,所以我们可以使用它们将轮廓进一步分类为边缘,暗线或亮线。沿主要方向的转向G2和H2给出轮廓点的相位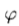
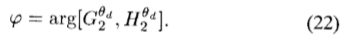
为了优先选择线条或边缘,我们按相位偏好因子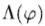 缩放了能量幅度E2(
缩放了能量幅度E2( d)
d)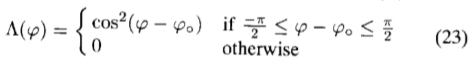
其中
阈值处理阶段与以前一样进行。图13示出了这样的处理的结果,选择(d)中的暗线和(e)中的边缘。 (正方形上的斑点是由于单个点上的多个方向所致,可以由后期处理稀疏运算符将其删除。)
D.阴影形状分析
Pentland [35]观察到,在许多情况下,表面的反射率函数近似线性,在这种情况下,距离图像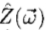 的傅立叶变换与强度图像
的傅立叶变换与强度图像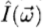 的傅立叶变换有关。通过线性变换,包括根据频率改变相位和缩放比例
的傅立叶变换有关。通过线性变换,包括根据频率改变相位和缩放比例

其中,wl是在光源方向上频率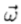 的分量。在这种情况下,阴影形状的分析可以通过Pentland在傅里叶域中实现的过滤操作来执行。他还指出,使用类似Gabor的滤波器可以完成相同过程的局部近似。
的分量。在这种情况下,阴影形状的分析可以通过Pentland在傅里叶域中实现的过滤操作来执行。他还指出,使用类似Gabor的滤波器可以完成相同过程的局部近似。
我们可以从阴影中描述这种形状,如下所示:感兴趣的表面Z(x,y)被认为是基本小波的总和,我们可以称其为“小块” bj(x,y)。阴影处理将这些小波变换为一组新的基本小波,我们可以将其称为“阴影” sj(x,y)。根据(25)的转换,每个子项与它的阴影相关:bj(x,y)→sj(x,y)。由于此着色过程是线性的,因此保持了叠加,并且很容易从观察到的强度图像转换回基础范围图像。只需将强度图像 I(x,y)分解为阴影系数aj: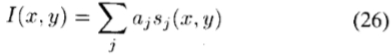
并使用这些系数以子集基础集重建感兴趣的表面: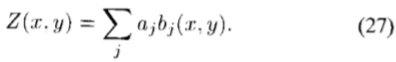
上述的可操纵金字塔为实现此目标提供了一种方便的方法。图7的可转向滤波器是阴影。根据(25)缩放比例的可控正交对配对近似于相应的凸点。
由于可控金字塔变换是自反转的,因此应用阴影滤波器可以得出系数aj。可操纵性使人们可以轻松适应不同的照明方向,从而确定哪个子弹片对应于哪个阴影。图14显示了使用图7中所示的金字塔分解应用的阴影形状算法。范围图像成功捕获了对象遗物的基本特征。

图14:(a)使用可控图像变换进行阴影阴影线性分析的图像输入。 (使用转向来适应不同的光线方向):(b)生成的距离图显示为低分辨率3-D图; (c)像素强度显示表面高度的相同范围图。 这种简单的机制使用生物学上合理的滤镜,可以正确得出图像表面特征。
VI 三维可转向滤光片
体积空间数据和时间图像序列需要三维处理。与二维数据一样,滤波器自适应定向的能力有很多应用(例如[20])。对于图像的时间序列,时空方向对应于速度[1];因此,我们希望可转向滤波器在运动分析中很有用。
在三个维度中,我们希望求解的转向方程
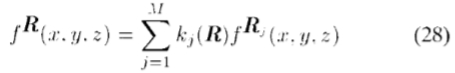
在应用三维旋转R后要解决的情况下,fR(x,y,z)为f(x,y,z),每个Rj标识第j个基准的方向功能。
在二维中,所需基本滤波器的数量取决于函数的角傅立叶分解中存在的不同正弦波的数量。在三个维度上,我们可以在一系列球谐函数中进行类似的扩展。球谐函数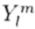 形成了球上函数的完整的正交基[7],[29],并广泛用于量子力学(它们是角动量算符的本征函数)。球谐函数的旋转公式[7]显示,阶为l 的2l + 1个球谐函数的线性组合可以合成任何球谐函数
形成了球上函数的完整的正交基[7],[29],并广泛用于量子力学(它们是角动量算符的本征函数)。球谐函数的旋转公式[7]显示,阶为l 的2l + 1个球谐函数的线性组合可以合成任何球谐函数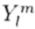 的任意旋转。
的任意旋转。
与在二维情况下一样,为写为多项式乘窗函数的函数开发控制公式很方便。作为过滤器的特别感兴趣的是具有旋转对称轴的功能。这些函数通过变换R旋转,使其对称轴沿余弦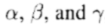 方向指向,可以表示为
方向指向,可以表示为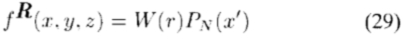
其中W(r)是任何球对称函数,r = 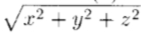 是PN(x')中的N阶多项式
是PN(x')中的N阶多项式
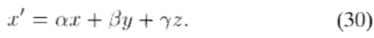
将函数形式(29)代入三维操纵方程(28)后,可以得出以下多项式定理,用于将轴对称函数写成多项式乘以球对称窗函数(有关证明,请参阅附录E)。
定理4:给定三维轴对称函数f(x,y.z)= W(r)PN(x),其中PN(x)是x中的偶数或奇数对称N阶多项式。设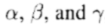 为fR(r,y.z)对称轴的方向余弦,而
为fR(r,y.z)对称轴的方向余弦,而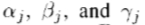 为fRj(r,y.z)对称轴的方向余弦。然后,转向方程
为fRj(r,y.z)对称轴的方向余弦。然后,转向方程
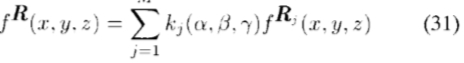
仅当且仅当
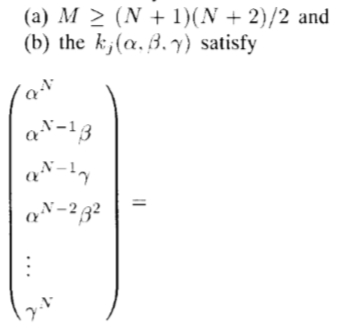
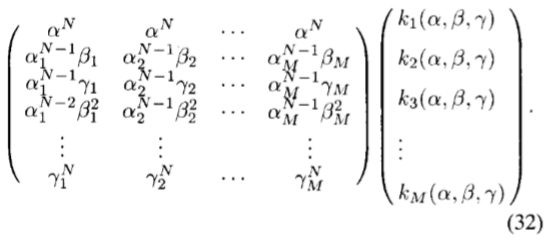
通过添加足以操纵偶数和奇数对称多项式的基函数的数量,从定理4可以得出:(N + 1)2个基函数足以操纵f(x,y,z)= W(r)PN( x),其中PN(x)是一般的N阶多项式。定理4允许设计和操纵任意轴向对称的三维滤波器。例如,可以设计高斯G2的二阶导数的三维版本,并为其希尔伯特变换H2拟合三阶多项式最小二乘。由于G2可以写为高斯窗函数的二阶偶校验多项式,因此根据定理4,六个基函数足以将其控制在三个维度上。十个基本函数将控制H2。
三维过滤可能需要大量计算。对于不可分离的内核,计算成本随着内核大小的立方而增长。但是,对于可分离的内核,成本仅随内核大小线性增长。因此,开发x-y-z可分离的可转向滤波器很重要。球对称高斯函数可以写为x,y和z的乘积。 如果加权函数W(r)是高斯函数,则通过将(30)替换为(29)中的x,可以将(29)形式的函数fR(x,y,z)写为可分离基函数的和。 。
Ⅶ 总结
可控滤镜可用于涉及定向滤镜的各种操作。旋转至任意角度的定向滤镜形成为基础滤镜的线性组合。一旦知道了基本滤波器的响应,就可以轻松找到转向(旋转)到任意角度的滤波器的响应。可以使用类似的技术来控制滤波器的相位。我们已经表明,给定足够的基本滤波器,大多数滤波器可以用这种方式进行控制,并且我们已经描述了如何确定所需的基本函数的最小数量以及如何在角度之间进行插值。可控滤镜可应用于早期视觉和图像分析中的许多问题。由于旋转滤镜的合成是分析性和精确的,因此与组合定向滤镜在不同方向上的临时方法相比,可控滤镜为图像分析提供了优势。
我们设计了可控正交对滤波器,并使用它们来分析方向,自适应滤波以增强方向结构并检测轮廓。这些处理方案在初始通过基本滤波器后不需要额外的卷积。轮廓检测器利用正交对以单个响应标记线条和边缘,并可用于将轮廓进一步分类为暗线,亮线或边缘。
人们还可以构建自相似的可控金字塔表示,可以将其视为可控小波变换,从而允许在所有尺度上分析和操纵定向结构。可操纵的金字塔可用于局部线性阴影形状分析。转向性能可适应照明方向。
转向可概括为三个维度,我们给出了用于转向任意旋转对称函数的公式。基函数可以在x-y-z中分离,从而为大型滤波器提供了巨大的计算优势。这些3-D滤波器应在运动分析和体积数据分析中找到应用。
附录A
定理证明1
将f(r, )(9)的展开代入转向约束(8),并将两侧投影到 -N<=m<=N 的复指数
)(9)的展开代入转向约束(8),并将两侧投影到 -N<=m<=N 的复指数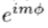 上,得出一组联立线性方程组:
上,得出一组联立线性方程组:
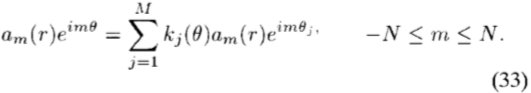
如果am(r)= 0大约m,那么我们可以从集合中删除该约束; 否则,将两边除以am(r)。 上面的约束对于-m和m是相同的; 因此,在不失一般性的情况下,我们仅考虑(33)中的 0≤m≤N 的正频率。 这给出了定理1的(10)。一个人也可以从(33)开始并从中推导操纵条件,这表明该定理的结论在且仅当前提成立时成立。
附录B
定理证明2
我们希望找到可以覆盖给定滤波器f(r, )的所有旋转的最小数量的基本滤波器。 令gj(r,
)的所有旋转的最小数量的基本滤波器。 令gj(r, ),0≤j≤M 是M个基函数的任意集合。 我们想要找到满足(11)的最小数M。 使用f(r,
),0≤j≤M 是M个基函数的任意集合。 我们想要找到满足(11)的最小数M。 使用f(r, )(9)的展开式,将(11)的两侧投影到
)(9)的展开式,将(11)的两侧投影到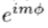 上,并除以am(r)
上,并除以am(r)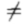 0得出以下约束:
0得出以下约束:
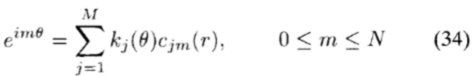
其中cjm(r)是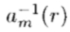 乘以基函数gj(r,
乘以基函数gj(r, )在
)在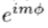 上的投影。
上的投影。
将(34)代入复指数的正交关系中,我们可以编写以下矩阵方程:
其中,I 是一个T乘T恒等矩阵; C是具有元素clj(r)的T乘M矩阵; K为M乘M,元素为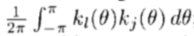 ; Ct为C转置; T为am(r)
; Ct为C转置; T为am(r)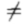 0的正或负频率m的数量。
0的正或负频率m的数量。
由于I 的等级为T,因此K必须至少等级为T;因此,为了进行转向,我们必须根据需要设置M>=T。
附录C
定理证明3
考虑术语ckyn-k,其中0≤k≤n。 可以使用x = rcos( )和y = rsin(
)和y = rsin( )在极坐标中重写
)在极坐标中重写
可以证明,以傅立叶级数表示的正弦和余弦幂的乘积只能包含频率n ,(n-2)
,(n-2) ,...,-(n-2)
,...,-(n-2) ,-n
,-n 。 因此,对于-N≤m ≤N而言,仅包含偶数项的N阶多项式只能具有偶数角频率m。 根据定理1,最多需要N + 1个基函数进行操纵。 类似地,N + 1个基函数对于仅具有奇校验位的多项式就足够了。 一般的N阶多项式可以包含绝对值小于或等于N的所有角频率,并且最多需要2N + 1个基函数来进行转向。
。 因此,对于-N≤m ≤N而言,仅包含偶数项的N阶多项式只能具有偶数角频率m。 根据定理1,最多需要N + 1个基函数进行操纵。 类似地,N + 1个基函数对于仅具有奇校验位的多项式就足够了。 一般的N阶多项式可以包含绝对值小于或等于N的所有角频率,并且最多需要2N + 1个基函数来进行转向。
附录D
X和y可分隔的基础函数
我们展示了如何找到一些多项式滤波器的转向公式和x-y可分离基函数,我们仅考虑偶数或奇数奇偶校验滤波器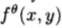 的情况,可以写成
的情况,可以写成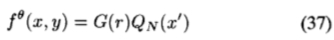
其中G(r)是高斯函数(因此x-y可分离),而QN(x')是N中的N阶多项式
根据定理3,N + 1个函数可以构成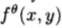 的基集。 我们假设存在一个N + 1个x-y可分离滤波器的基集(并非对所有函数都成立)。 然后会有一些可分离的基函数Rj(x)Sj(y)
的基集。 我们假设存在一个N + 1个x-y可分离滤波器的基集(并非对所有函数都成立)。 然后会有一些可分离的基函数Rj(x)Sj(y)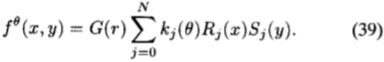
通过将(37)中的x和y的最高阶乘积与(39)的高阶乘积相等,即x(N-j)yj 其中 0≤j≤N的系数,可以找到内插函数kj( )。 )到(37)中,fe(r,y)中的(x')N项将产生N + 1个x和N 个y的不同乘积,因为
)。 )到(37)中,fe(r,y)中的(x')N项将产生N + 1个x和N 个y的不同乘积,因为
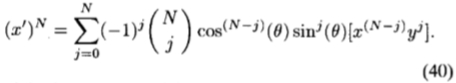
每个基函数Rj(x)Sj(y)只能贡献n阶的x和y的幂的乘积(否则,Rj(x)Sj(y)将是r和y的阶高的多项式N)。 因此,我们必须
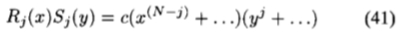
其中c是常数。 因此,(39)表明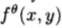 中最高阶项x(N-j)yj的系数为kj(
中最高阶项x(N-j)yj的系数为kj( )。 (低阶项可以出现在多个可分离的基函数中;因此,它们的系数将是不同的kj(
)。 (低阶项可以出现在多个可分离的基函数中;因此,它们的系数将是不同的kj( )的总和。)使用(37)中的(40)得出正弦和余弦的系数相同。 两者相等
)的总和。)使用(37)中的(40)得出正弦和余弦的系数相同。 两者相等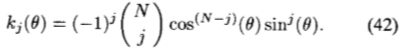
为了从原始滤波器f(x,y)中找到可分离的基函数Rj(x)Sj(y),我们注意到从可分离的基函数(39)的转向方程中,我们有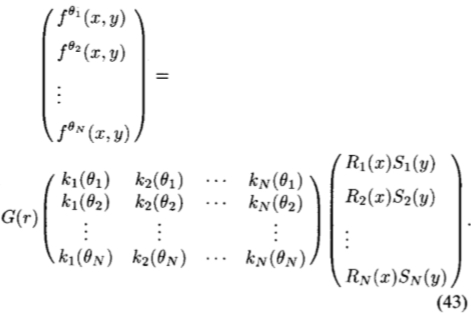
通过将(43)右边的k( )的矩阵求逆,Rj(x)Sj(y)可以写为
)的矩阵求逆,Rj(x)Sj(y)可以写为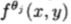 的线性组合。
的线性组合。
附录E
定理证明4
首先,仅等于(31)的最高阶项(将两边除以W(r)之后),我们得到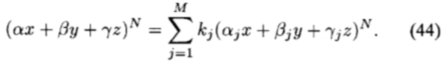
扩展两侧求和的N次方,并等于x,y和z的幂,得出约束(32)。
由(31)中的任何低阶多项式fR和fRj得出的约束方程将线性依赖于(32)的约束。 可以看出如下。 对于p + g + r <N,考虑(31)中的xpyqzr的系数。 排除共同因素,我们有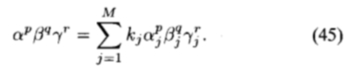
因为假定PN(x')具有偶数或奇数对称性,所以x' 的幂只能相差偶数个整数。 考虑由(31)阶p + g + r + 2中的项得出的系数。 至少将存在以下三个方程式:
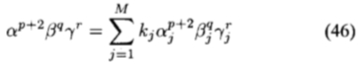
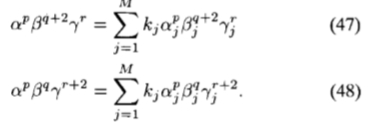
现在利用方向余弦的平方和为1的事实:将 和
和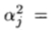
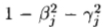 代入(46),然后将(47)和(48)相加得到(45) )。因此,由多项式阶数n的项得出的每个约束方程均线性地依赖于多项式阶数n + 2的约束方程式,因此,如果满足最高阶项(32)的约束且多项式PN(x ')包含偶数或奇数阶的项,则(31)成立,因为(32)中有(N + 1)(N + 2)/ 2个约束方程,我们必须有M>=(N + 1)(N +2)/ 2。一个人可以从(32)回到(31),因此,当且仅当前提成立时,定理结论成立。
代入(46),然后将(47)和(48)相加得到(45) )。因此,由多项式阶数n的项得出的每个约束方程均线性地依赖于多项式阶数n + 2的约束方程式,因此,如果满足最高阶项(32)的约束且多项式PN(x ')包含偶数或奇数阶的项,则(31)成立,因为(32)中有(N + 1)(N + 2)/ 2个约束方程,我们必须有M>=(N + 1)(N +2)/ 2。一个人可以从(32)回到(31),因此,当且仅当前提成立时,定理结论成立。
附录F
指导偶数或奇偶校验多项式的公式
表Ⅰ
需要根据基础函数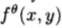 合成
合成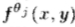 的(8)中的插值函数kj(
的(8)中的插值函数kj( ),其中f(x,y)是一个多项式x和y(是任何窗口函数W( r))
),其中f(x,y)是一个多项式x和y(是任何窗口函数W( r))
仅具有偶数或奇偶校验条款。 (假设n + 1个基函数的方向在0和Π 之间均匀间隔,即 j=(j-1)Π /(n + 1),其中 j = 1,2,... n + 1。在这些条件下,术语中显而易见的模式将继续适用于所有多项式。)
j=(j-1)Π /(n + 1),其中 j = 1,2,... n + 1。在这些条件下,术语中显而易见的模式将继续适用于所有多项式。)

附录G
可转向正交滤波器对
表Ⅱ
几个高斯导数和多项式拟合它们的希尔贝克变换(沿X轴进行的变换和导数)。 (对所列函数进行了规范化处理,以使它们平方的所有空间上的积分等于1。要操纵每个函数,请使用(8)和表1中的相应kj( )。)
)。)


图15:三对可控正交滤波器对,列于表Ⅱ。
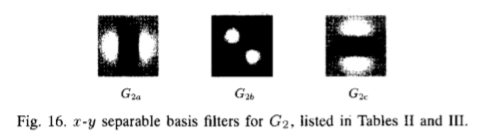
图16:G2的x-y可分离基本滤波器,在表II 和表Ⅲ 中列出
表Ⅲ
高斯第二阶导数的x-y可分离基集和插值函数。 (要创建沿角度 旋转的高斯二阶导数,请使用:
旋转的高斯二阶导数,请使用: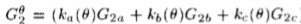 )。kb(
)。kb( )中的负号选择方向 正
)中的负号选择方向 正 表示逆时针旋转。)
表示逆时针旋转。)

表 Ⅳ
G2 x-y可分离基组的9—TAP过滤器。 (滤镜f1 和f2 具有偶数对称性; f3具有奇数对称性。这些滤镜取自表III,采样间隔为0.67。使用表Ⅲ 的插值函数。)
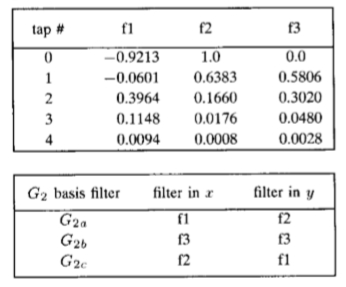
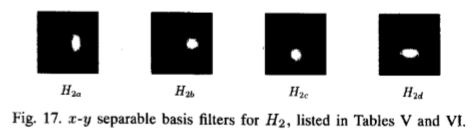
图17:H2的x-y可分离基本滤波器,在表V和Ⅵ中列出

图18:G4的x-y可分离基本滤波器,列于表VIl和Ⅷ
表Ⅴ
H2基集:高斯第二导数的Hilbert变换的x-y可分离基集和内插函数。 (要合成沿方向 定向的过滤器,请使用:
定向的过滤器,请使用: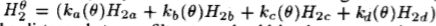 。
。
滤波器抽头之间的距离应与高斯滤波器的正交对导数使用的距离相同。)

表 Ⅵ
用于H2的x-y可分离基础集的9-TAP过滤器。 (抽头0为0.0的滤波器具有大约抽头0的奇对称性;其他滤波器具有偶数对称。这些滤波器取自表V,样本间距为0.67。使用表V的插值函数。)
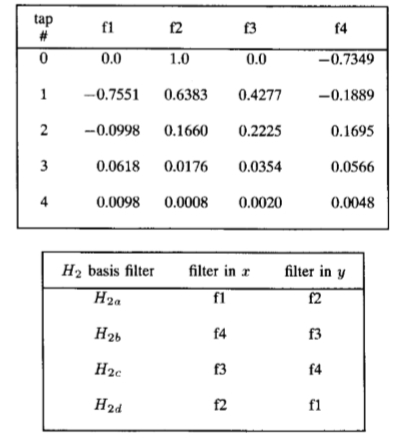
表 Ⅶ
高斯四阶导数的X-Y可分离基集和插值函数。 (要创建旋转角度为 的高斯的四阶导数,请使用:
的高斯的四阶导数,请使用: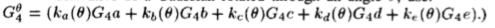 )
)

表 Ⅷ
G4的x-y可分离基础集的13-TAP滤波器。(抽头0为0.0的滤波器关于抽头0具有奇数对称性;其他具有偶数对称性。这些滤波器取自表Vll,采样间隔为0.5。 表VII的内插函数。)


图19:表IX和表X中列出的H4的x-y可分离基础文件。
表 IX
H4:基数集:x-y可分离基数集和高斯四阶导数的Hilbert变换拟合的插值函数。 (要合成沿方向 定向的滤波器,请使用:
定向的滤波器,请使用: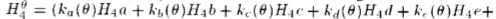
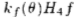 )。
)。
尽管H4函数不能精确地x-y分离,但是这些可分离函数非常接近H4。)

表 X
H4的x-y可分离基础集的13-TAP过滤器。 (抽头0为0.0的滤波器具有大约抽头0的奇对称性;其他滤波器具有偶数对称。这些滤波器取自表IX,采样间隔为0.5。使用表IX的插值函数。)
附录一
G2和H2定向能的傅里叶级数的低阶术语
表 ⅩⅠ
G2,H2正交滤镜对的F型傅里叶定向能量E,是角度 的功能。 (G2a,G2b,…和H2a,H2b,…是 表 IV和VI 中列出的x-y可分离基滤波器的输出,
的功能。 (G2a,G2b,…和H2a,H2b,…是 表 IV和VI 中列出的x-y可分离基滤波器的输出, = 0是垂直方向,并沿逆时针方向增加。)
= 0是垂直方向,并沿逆时针方向增加。)

致谢
作者与J. Bergen,D。Heeger,J.Koenderink,J.Lubin,A.Pentland,R.Picard和E.Simoncelli进行了有益的对话。 我们感谢G.E. Medical Systems(密尔沃基)的P.Granfors提供了图12(a)的数字心脏血管造影照片。 我们感谢匿名裁判的意见,这对本文有所改善。
参考文献
[1] E.H.Adelson and J.R.Bergen, "Spatiotemporal energy models for the perception of motion." J.Opt.Soc.Am.A,vol.2,no.2, pp.284-299, 1985.
[2] E.H.Adelson.E.Simoncelli,and R.Hingorani, “Orthogonal pyramid transforms for image coding." in Proc.SPIE-Vis.Comm.Image Proc. ll,1987,pp.50-58.
[3] A.C.Bovik, “Multichannel texture analysis using localized spatial filters,”IEEE Patt.Anal. Machine Intell,vol.12,no.1,pp.55-73, 1990.
[4] R.N.Bracewell,The Fourier Transform and its Applications.New York: McGraw-Hill,1978.
[5] P.J.Burt and E.H.Adelson, "The Laplacian pyramid as a compact image code.” IEEE Trans. Commun,vol.31,no.4,pp.532-540.1983.
[6] J.F.Canny, "A computational approach to cdge detection." IEEE Pat. Anal.Machine Intell, vol.8,no.6,pp.679-698,1986.
[7] R.Courant and D. Hilbert, Methods of Mathematical Physics, vol.1. New York:Wiley Interscience,1953.
[8] P.Daniclsson and O.Seger. “Rotation invariance in gradient and higher order derivative detectors," Comp. Vision Graphics Image Processing,vol.49,pp.198-221,1990.
[9] J.G.Daugman,"Complete discrete 2-d Gabor transforms by neural networks for image analysis and compression,IEEE Trans.Acoust. Speech Signal Proc, vol.36,no.7,pp.1169-1179,1988.
[10] D.Esteban and C.Galand, "Application of quadrature mirror filters to split band voice coding schemes, in Proc.ICASSP,1977,pp.191-195.
[11] D.Fleet and A.Jepson, "Computation of normal velocity from local phase information," in Proc.IEEE CVPR(San Diego,CA),1989,pp. 379-386.
[12] W.T.Freeman and E.H.Adelson, “Steerable filters," in Topical Mtg. Image Understanding Machine Vision.Opt.Soc.Amer.,Tech.Digest Series, vol.14, June 1989.
[13] ——, "Steerable filters for early vision,image analysis,and wavelet decomposition," in Proc.3rd It.Conf.Comput.Vision (Osaka,Japan), 1990.
[14] G.H.Granlund,“In search of a general picture procesing operator.” .Coyp.Graphics lmage Processing,vol.8,pp.155-173,1978.
[15] A.Grossmann and J.Morlet,“Decomposition of Hardy functions into square integrable wavelets of constant shape,"SIAM J.Math,vol.15, pp.723-736,1984.
[16] R.M.Haralick,"The digital step edge from zero crossings of second directional derivatives,"IEEE Patt.Anal.Machine Intell,Vol.6,no.1, pp.58-68,1984.
[17] D.1.Hecger."Optical flow using spatiotemporal filters,"Int.J.Comp. .Vision,vol.1,no.4,pp.279-302,1988.
[18] M.Kass and A.Witkin,"Analyzing oriented patterms,"Comp.Vision Graphics lmage Processing,vol.37,pp.362-385,1987.
[19] H.Knutsson and G.H.Granlund,"Texture analysis using two. dimensional quadrature filters,"in IEEE Comput.Soc.Workshop Comp. Architecture Patt.Anal.Image Database Mgmt,1983,pp.206-213.
[20] H.Knutsson,L.Haglund,and G.H.Granlund,“Tensor fheld controlled image sequence enhancement,"in SSAB Symp.Image Anal.(Linkoping. Sweden),Mar.1990.
[21] H.Knutsson,R.Wilson,and G.H.Granlund,"Anisotropic nonstationary image estimation and its applications:Part 1-Restoration of noisy images,”IEEE Trans.Commun.,vol.31,no.3,pp.388-397,1983.
[22] J.J.Koenderink,"Design for a sensorium,”in W.von Seelen,B.Shaw. and U.M.Leinhos(Eds.),Org.Neural Networks,Verlagsgeselschaft mbH,1988,pp.185-207.
[23] ——,"Operational significance of receptive field assemblies,"Biol. Cybern,vol.58,pp.163-171,1988.
[24] J.J.Koenderink and A.J.van Doorm,“Representation of local geometry in the visual system,"Biol.Cybern.,vol.55,pp.367-375,1987.
[25] J.Lim,Two-Dimensional Signal and image Procesing.Englewood Cliffs,NJ:Prentice-Hall,1990.
[26] S.G.Mallat,"A theory for multiresolution signal decomposition:The wavelet representation,”IEEE Pat.Anal.Machine Intell,vol.11,no. 47,pp.674-693,1989.
[27] J.B.Martens,"Applications of polynomial transforms in image coding and computer vision,"in Proc.SPIE(Cambridge,MA),1989,vol.1199, pp.1279-1290.
[28] "The Hermite transform-Theory,IEEE Trans.Acoust.Speech Signal Proc,vol.38,no.9,pp.1595-1606,1990.
[29] E.Merzbacher,Quantum Mechanics.New York:Wiley,1970.
[30] M.C.Morrone and D.C.Burr,“Feature detection in human vision:A phase-dependent energy model,"Proc.R.Soc.London B,vol.235,pp. 221-245,1988.
[31] M.C.Morrone and R.A.Owens,“Feature detection from local energy, Patt.Recog.Lett.,vol.6,pp.303-313,1987.
[32] P.M.Morse and H.Feshback,Methods of Theoretical Physics,vol.1. New York:McGraw-Hill,1953.
[33] A.V.Oppenheim and R.W.Schafer,Digital Signal Processing. Englewood Cliffs,NJ:Prentice-Hall,1975.
[34] A.P.Pentland,"Local shading analysis,”IEEE Patt.Anal. Machine Intell.,vol.6,no.2,pp.170-187,1984.
[35] ——,"Linear shape from shading"lnt.J.Comp.Vision,vol.1,no.4, pp.153-162,1990.
[36] p.Perona,“Finite representation of deformable functions,"Tech.Rep. 90-034,Int.Comput.Sci.Inst.,Berkeley,CA,1990.
[37] P.Perona and J.Malik,“Detecting and localizing edges composed of steps,peaks and roofs,"in Proc.3rd Int.Conf. Comput.Vision (Osaka, Japan),1990.
[38] T.Sanger,"Stereo disparity computation using Gabor filters."Biol Cybern.,vol.59,pp.405-418,1988.
[39] E.P.Simoncelli and E.H.Adelson,"Non-separable extensions of quadrature mirror filters to multiple dimensions,"Proc.IEEE,vol.78, no.4,pp.652-664,1990.
[40] ——,Subband transforms,"in J.W.Woods(Ed.),Subband lmage Coding.Norwell,MA:Kluwer,1990,ch.4.
[41] E.P.Simoncelli,W.T.Freeman,E.H.Adelson,and D.J.Heeger, “Shiftable multi-scale transforms,"Vision Modeling Tech.Rep.161, .Media Lab.,Mass.Inst.Technol.,Cambridge.MA.1991.
[42] M.Veterli,"Multidimensional subband coding:Some theory and algorithms,”Signal Processing,vol.6,no.2,pp.97-112,1984.
[43] A.B.Watson,"The cortex transform:Rapid computation of simulated neural images,"Comput.Vision Graphics lImage Processing,vol.39, pp.311-327,1987.
[44] J.W.Woods and S.D.O'Neil,"Subband coding of images,"IEEE .Trans.Acoust.Speech Signal Proc.,vol.34,no.5,pp.1278-1288,1986.
[45] R.A.Young,"Simulation of human retinal function with the Gaussian derivative model,in PrOc.IEEE Comput.Soc.Conf. Comput.Vision Patt. Recog.,1986,pp.564-569,1986.
[46] S.W.Zucker,“Early orientation selection:Tangent fields and the dimensionality of their support,"Comp.Vision.Graphics lImage Processing. vol.32,pp.74-103,1985.




















 1138
1138

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








