PAT-2019年冬季考试-甲级 7-4 Cartesian Tree (30分)——小根堆的中序遍历求层序遍历

7-4 Cartesian Tree (30分)

A Cartesian tree is a binary tree constructed from a sequence of distinct numbers. The tree is heap-ordered, and an inorder traversal returns the original sequence. For example, given the sequence { 8, 15, 3, 4, 1, 5, 12, 10, 18, 6 }, the min-heap Cartesian tree is shown by the figure.

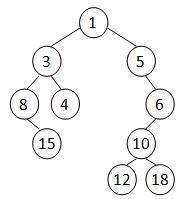
Your job is to output the level-order traversal sequence of the min-heap Cartesian tree.

Input Specification:
Each input file contains one test case. Each case starts from giving a positive integer N (≤30), and then N distinct numbers in the next line, separated by a space. All the numbers are in the range of int.

Output Specification:
For each test case, print in a line the level-order traversal sequence of the min-heap Cartesian tree. All the numbers in a line must be separated by exactly one space, and there must be no extra space at the beginning or the end of the line.

Sample Input:

10
8 15 3 4 1 5 12 10 18 6

Sample Output:

1 3 5 8 4 6 15 10 12 18

题意：

7-4笛卡尔树（30分）

笛卡尔树是由一系列不同的数字构成的二叉树。树是按堆排序的，按顺序遍历返回原始序列。例如，给定序列{8、15、3、4、1、5、12、10、18、6}，最小堆笛卡尔树如图所示。

您的工作是输出最小堆笛卡尔树的级别顺序遍历序列。

输入规格：

每个输入文件包含一个测试用例。每种情况从给出一个正整数N（≤30）开始，然后在下一行中给出N个不同的数字，用空格隔开。所有的数字都在整数范围内。

输出规格：

对于每个测试用例，一行打印最小堆笛卡尔树的级别顺序遍历序列。一行中的所有数字必须用一个空格隔开，并且行的开头或结尾不能有多余的空格。

思路：

利用最小堆的性质，根为当前子树最小的值，得到根的下标，而中序遍历为LNR，得到根下标即可分开左子树和右子树。