递归算法及例题入门

全文参考自bilibili作者连烟
算法笔记总目录

一、概述

1 . 概念

• 编程语言中，函数Func(Type a,……)直接或间接调用函数本身，则该函数称为递归函数。
• 一种计算过程，如果其中每一步都要用到前一步或前几步的结果，称为递归的。用递归过程定义的函数，称为递归函数，例如连加、连乘及阶乘等。凡是递归的函数，都是可计算的，即能行的。

2 . 递归调用原理
递归调用原理视频讲解地址
函数调用栈实例：主函数main()调用funcA()，funcA()调用funcB()，funcB()再自我调用（递归）

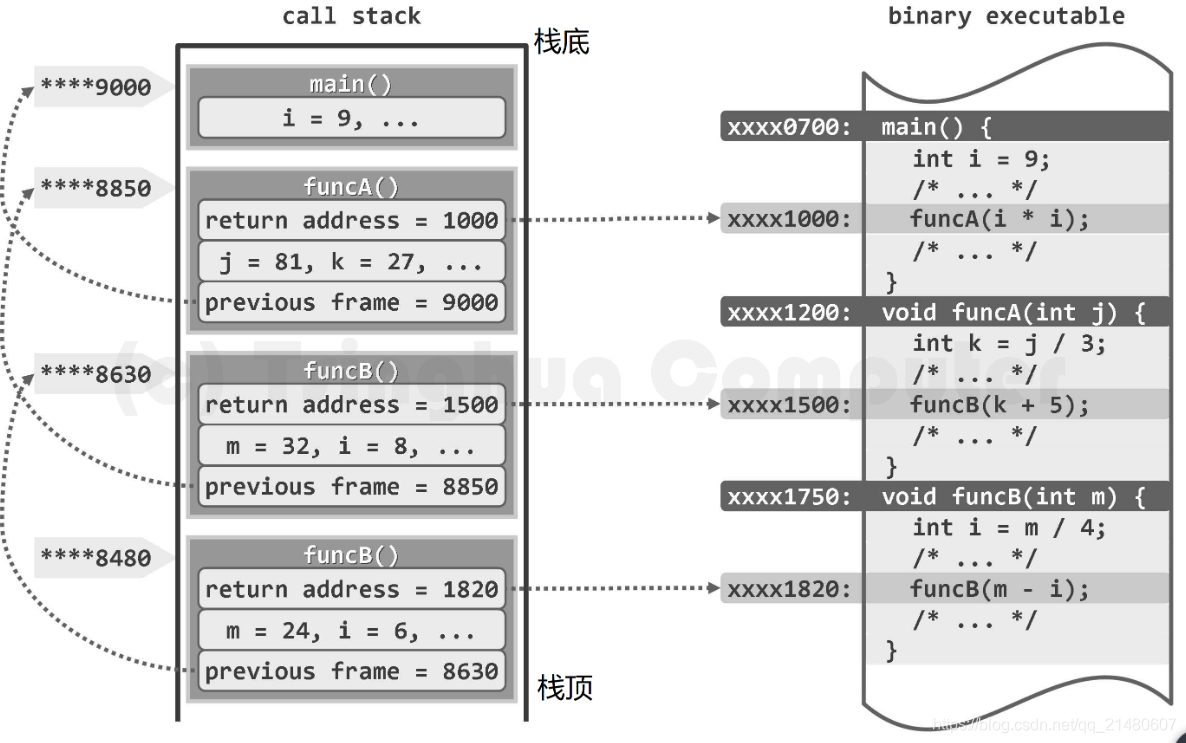
函数调用栈的基本单位是帧（frame）。每次函数调用时，都会相应地创建一帧， 记录该函数实例在二进制程序中的返回地址（return address），以及局部变量、传入参数等， 并将该帧压入调用栈。若在该函数返回之前又发生新的调用，则同样地要将与新函数对应的一帧压入栈中，成为新的栈顶。函数一旦运行完毕，对应的帧随即弹出，运行控制权将被交还给该函 数的上层调用函数，并按照该帧中记录的返回地址确定在二进制程序中继续执行的位置。

在任一时刻，调用栈中的各帧，依次对应于那些尚未返回的调用实例，亦即当时的活跃函数实例（active function instance）。特别地，位于栈底的那帧必然对应于入口主函数main()， 若它从调用栈中弹出，则意味着整个程序的运行结束，此后控制权将交还给操作系统。

此外，调用栈中各帧还需存放其它内容。比如，因各帧规模不一，它们还需记录前一帧的起始地址，以保证其出栈之后前一帧能正确地恢复。

作为函数调用的特殊形式，递归也可借助上述调用栈得以实现。比如在上图中，对应于 funcB()的自我调用，也会新压入一帧。可见，同一函数可能同时拥有多个实例，并在调用栈中 各自占有一帧。这些帧的结构完全相同，但其中同名的参数或变量，都是独立的副本。比如在 funcB()的两个实例中，入口参数m和内部变量i各有一个副本。

3 . 递归三要素及关键点
三要素：

1. 一定有一种可以退出程序的情况；
2. 总是在尝试将一个问题化简到更小的规模
3. 父问题与子问题不能有重叠的部分

关键点：1.确定好条件。2.找到循环的是哪些。

• 边界条件：确定递归到何时终止，也称为递归出口。
• 递归模式：大问题是如何分解为小问题的，也称为递归体。递归函数只有具备了这两个要素，才能在有限次计算后得出结果。

二、例题

1 . 计算阶乘(factorial)

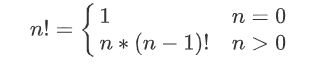
#include <stdio.h>

int fact(int n){
    if (n == 0) return 1;
    return n * fact(n - 1);
}

int main(){
    int ans = fact(10); //调用（递归）函数
    printf("%d\n", ans);
    return 0;
}

计算斐波那契数列

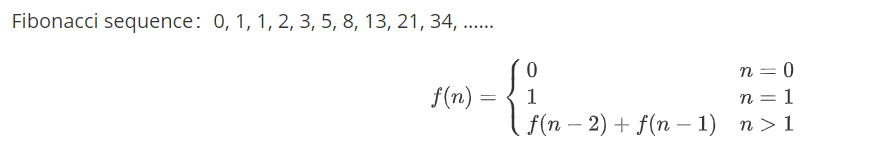
#include <stdio.h>

int fib(int n) {
    if (n == 0) return 0;
    if (n == 1) return 1;
    return fib(n - 2) + fib(n - 1);
}

int main() {
    for (int i = 0; i < 10; i++) {
        printf("%d ", fib(i));
    }
    printf("\n");
    return 0;
}