分治算法_适用于分治法求解的问题,经分解得到的子问题往往是相互独立的-优快云博客

本文深入探讨分治算法的设计思想，列举其适用条件，并通过经典问题如二分搜索、大整数乘法、Strassen矩阵乘法等进行实例解析。同时，文章详细介绍了分治法的基本步骤，复杂性分析，以及设计程序时的思维过程。

概述参考博客地址
 算法笔记总目录

一、分治算法的设计思想：

分–将问题分解为规模更小的子问题；
治–将这些规模更小的子问题逐个击破；
合–将已解决的子问题合并，最终得出“母”问题的解；

减而治之（每次让问题的规模减1）
分而治之（每次让问题的规模减半）（归并排序的思想）

二、分治法适用的情况

分治法所能解决的问题一般具有以下几个特征：

该问题的规模缩小到一定的程度就可以容易地解决
该问题可以分解为若干个规模较小的相同问题，即该问题具有最优子结构性质。
利用该问题分解出的子问题的解可以合并为该问题的解；
该问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子子问题。

第一条特征是绝大多数问题都可以满足的，因为问题的计算复杂性一般是随着问题规模的增加而增加；

第二条特征是应用分治法的前提它也是大多数问题可以满足的，此特征反映了递归思想的应用；、

第三条特征是关键，能否利用分治法完全取决于问题是否具有第三条特征，如果具备了第一条和第二条特征，而不具备第三条特征，则可以考虑用贪心法或动态规划法。

第四条特征涉及到分治法的效率，如果各子问题是不独立的则分治法要做许多不必要的工作，重复地解公共的子问题，此时虽然可用分治法，但一般用动态规划法较好。

三、可使用分治法求解的一些经典问题

（1）二分搜索
（2）大整数乘法
（3）Strassen矩阵乘法
（4）棋盘覆盖
（5）合并排序
（6）快速排序
（7）线性时间选择
（8）最接近点对问题
（9）循环赛日程表
（10）汉诺塔

四、分治法的基本步骤

分治法在每一层递归上都有三个步骤：

step1 分解：将原问题分解为若干个规模较小，相互独立，与原问题形式相同的子问题；

step2 解决：若子问题规模较小而容易被解决则直接解，否则递归地解各个子问题

step3 合并：将各个子问题的解合并为原问题的解。

它的一般的算法设计模式如下：

Divide-and-Conquer(P)

1. if |P|≤n0

2. then return(ADHOC(P))

3. 将P分解为较小的子问题 P1 ,P2 ,…,Pk

4. for i←1 to k

5. do yi ← Divide-and-Conquer(Pi) △ 递归解决Pi

6. T ← MERGE(y1,y2,…,yk) △ 合并子问题

7. return(T)

其中|P|表示问题P的规模；n0为一阈值，表示当问题P的规模不超过n0时，问题已容易直接解出，不必再继续分解。ADHOC(P)是该分治法中的基本子算法，用于直接解小规模的问题P。因此，当P的规模不超过n0时直接用算法ADHOC(P)求解。算法MERGE(y1,y2,…,yk)是该分治法中的合并子算法，用于将P的子问题P1 ,P2 ,…,Pk的相应的解y1,y2,…,yk合并为P的解。

五、分治法的复杂性分析

一个分治法将规模为n的问题分成k个规模为n／m的子问题去解。设分解阀值n0=1，且adhoc解规模为1的问题耗费1个单位时间。再设将原问题分解为k个子问题以及用merge将k个子问题的解合并为原问题的解需用f(n)个单位时间。用T(n)表示该分治法解规模为|P|=n的问题所需的计算时间，则有：

T（n）= k T(n/m)+f(n)

通过迭代法求得方程的解

六、依据分治法设计程序时的思维过程

实际上就是类似于数学归纳法，找到解决本问题的求解方程公式，然后根据方程公式设计递归程序。
1、一定是先找到最小问题规模时的求解方法
2、然后考虑随着问题规模增大时的求解方法
3、找到求解的递归函数式后（各种规模或因子），设计递归程序即可。

七、例题

更多例题

1.走楼梯

题目描述：
一个台阶总共有n级，如果一次可以跳1级，也可以跳2级。求总共有多少总跳法。
第一行输入T，表示有多少个测试数据。接下来T行，每行输入一个数n，表示台阶的阶数。
输出时每一行对应一个输出。

样例输入：
3
5
8
10

样例输出：
8
34
89

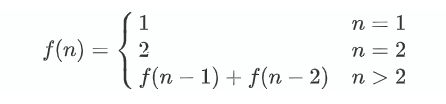
在这里插入图片描述

#include <stdio.h>

int solve(int n) {
	if (n == 1) return 1;
	if (n == 2) return 2;
	return solve(n - 1) + solve(n - 2);
}

int main() {
	int T;
	scanf("%d", &T);
	while (T--) {
		int n;
		scanf("%d", &n);
		int ans = solve(n);
		printf("%d\n", ans);
	}
	return 0;
}

2.全排列
博客讲解
题目描述：1234有多少种全排列

#include<string.h>
#include<stdio.h>
int k=0;
char a[100];
long long count=0;//全排列个数的计数
void s(char a[],int i,int k)//将第i个字符和第k个字符交换
{
    char t=a[i];
    a[i]=a[k];
    a[k]=t;
}
void f(char a[],int k,int n)
{
    if(k==n-1)//深度控制，此时框里面只有一个字符了，所以只有一种情况，所以输出
    {
       puts(a);
       count++;
    }
    int i;
    for(i=k;i<n;i++)
    {
        s(a,i,k);
        f(a,k+1,n);
        s(a,i,k);//复原，就将交换后的序列除去第一个元素放入到下一次递归中去了，递归完成了再进行下一次循环。这是某一次循环程序所做的工作，这里有一个问题，那就是在进入到下一次循环时，序列是被改变了。可是，如果我们要假定第一位的所有可能性的话，那么，就必须是在建立在这些序列的初始状态一致的情况下,所以每次交换后，要还原，确保初始状态一致。
    }
}
int main()
{
    gets(a);
    int l=strlen(a);//字符串长度
    f(a,k,l);
    printf("全排列个数:%lld\n",count);
    return 0;
}

3 . 二分搜索.
参考博客地址
给指定数字序列进行元素查找

/**
 * 二分查找 查找数字81
 */
public class TwoFenSearch3 {
 
    public static void main(String[] args) {
        int a[] = { 3,5,11,17,21,23,28,30,32,50,64,78,81,95,101};
        int target = 81;
        int start = 0;
        int end = a.length-1;
        int result = search(start,end,target,a);
        System.out.println(a[result]);
    }
 
    public static int search(int start,int end,int target,int a[]){
        if(start <= end) {
            int mid = (start + end) / 2;
            if (a[mid] == target) {
                return mid;
            } else if (target > a[mid]) {
                //target >和=都判断过了a[mid] 那么下次开始的位置应该越过mid的后一个位置
                return search(mid + 1, end, target, a);
            } else if (target < a[mid]) {
                //target <和=都判断过了a[mid] 那么下次结束的位置应该越过end到mid的前一个位置
                return search(start, mid - 1, target, a);
            }
        }
 
        return -1;
    }
}