数位dp-CodeForces - 55D-数%每位==0的个数，数位dp余数模板

最新推荐文章于 2022-01-26 23:31:56 发布

原创最新推荐文章于 2022-01-26 23:31:56 发布 · 279 阅读

1 ·

CC 4.0 BY-SA版权

数位dp 专栏收录该内容

6 篇文章

订阅专栏

博客围绕计算L到R区间内Beautiful numbers（能被自身所有非零数位整除的数）的数量展开。指出整除处理较难，通过取MOD（LCM{1,2,9}=2520）缩小范围，得出只需存x % MOD，还可对LCM{}离散化，用dp[20][3000][50]保存状态。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目链接：http://codeforces.com/problemset/problem/55/D
题目大意：Beautiful numbers定义：能被自身所有非零数位整除的数。就比如15是Beautiful numbers，因为15可以被1,5整除，14不是，因为14不能被4整除。

问：L到R区间内有多少个Beautiful numbers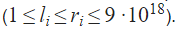 在这里插入图片描述
思路：
这个题就是整除比较难处理。

1： int MOD = LCM{1,2,9} = 5 * 7 * 8 * 9 = 2520
2：按照定义，数字x为Beautiful ： x % LCM{digit[xi]} = 0 即 x % MOD % LCM{digit[xi]} = 0，所以可以只需存x % MOD，范围缩小了。

那么统计已经出现的LCM{}和MOD就行了。
由2可以推出结论：n%a = (n%k * a)%a (k!=0)
a = LCM {}, 因为所有的LCM{}都是2520的因数。所以：2520=k * LCM{}。

我们要确定:n%LCM{}==0, 只要确定（n%2520）%LCM{}==0就可以了。

那么状态就很好表示了，只有保存n%2520就可以了。

这个前面不要13的倍数那道题用过。

当然LCM{}可以离散化一下，只有48个。

dp[20][3000][50]就可以保存所有的状态了。

#include <bits/stdc++.h>
#define LL long long
using namespace std;
const int mod=2520;

int a[20];
int index[3000];//1...9的各种lcm可以离散化处理，只有48个
LL dp[20][3000][50];
void LCMCSL()
{
    int cut=0;
    for(int i=1;i<=mod;i++)
    {
        if(mod%i==0)
        {
            index[i]=cut++;
        }
    }
}

LL LCM(LL a, LL b)
{
    if(a==0)
    {
        return b;
    }
    return a/__gcd(a, b)*b;
}

LL dfs(int pos, int mod, int Lcm, int mt)
{
    if(pos==-1)
    {
        return mod%Lcm==0;
    }

    if(!mt&&dp[pos][mod][index[Lcm]]!=-1)
    {
        return dp[pos][mod][index[Lcm]];
    }

    int Len=mt?a[pos]:9;
    LL ans=0;
    for(int i=0;i<=Len;i++)
    {
        ans+=dfs(pos-1, (mod*10+i)%2520, LCM(i, Lcm), i==a[pos]&&mt);
    }

    if(!mt)
    {
        dp[pos][mod][index[Lcm]]=ans;
    }

    return ans;

}

LL slove(LL x)
{
    int pos=0;
    while(x)
    {
        a[pos++]=x%10;
        x/=10;
    }

    return dfs(pos-1, 0, 1, 1);
}

int main()
{
    LCMCSL();
    int T;
    memset(dp, -1, sizeof(dp));
    scanf("%d",&T);
    while(T--)
    {
        LL L, R;
        scanf("%lld%lld",&L,&R);

        printf("%lld\n", slove(R)-slove(L-1));
    }

    return 0;
}