概率专题 dp: n个事件至少有k个事件成立的概率-优快云博客

本文链接：https://blog.youkuaiyun.com/qq_21433411/article/details/90143685

本文介绍了一种使用容斥原理和动态规划算法来计算飞机救援任务中至少k个发动机重启成功的概率的方法。通过分析每个救援队的成功概率，利用dp[i][j]表示前i个发动机能重启j个发动机的概率，最终求得dp[n][j]（k<=j<=n）的和即为所求概率。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目链接：https://ac.nowcoder.com/acm/contest/892/B
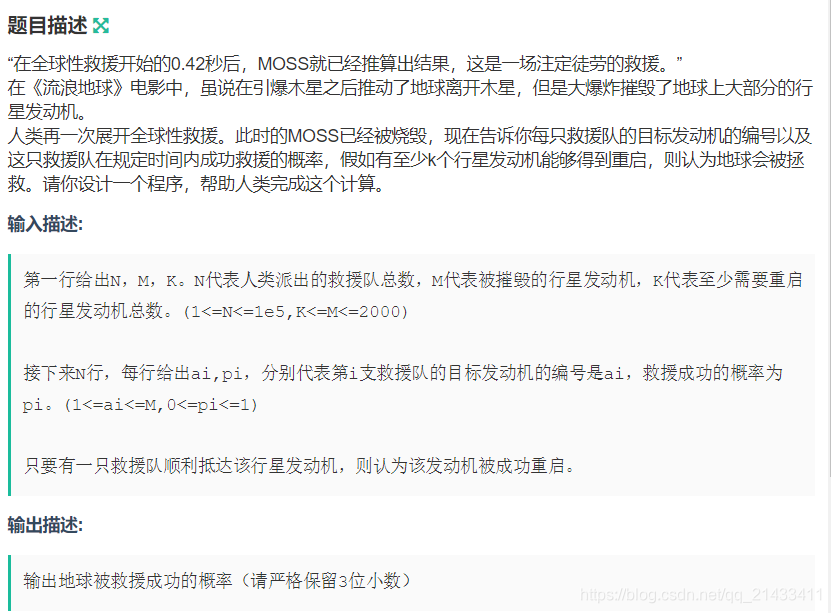
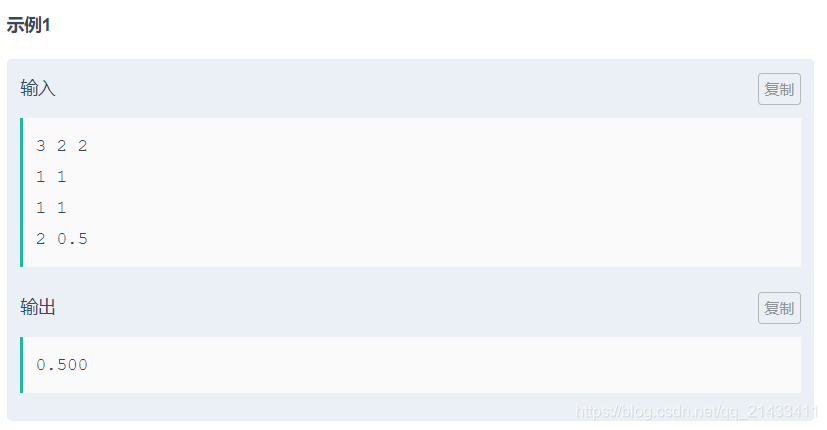
题目大意：
在这里插入图片描述

思路：
可以把每个发动机不能重启的概率求出来,每个救援队都不能成功。
用容斥求出成功的概率p[i]。

for(int i=1;i<=m;i++)
    {
        double s=1;
        for(int j=0;j<v[i].size();j++)
        {
            s*=(1-v[i][j]);
        }
        p[i]=1.0-(s);
    }

dp[i][j]表示前i个发动机能重启j个发动机的概率。

memset(dp, 0, sizeof(dp));
dp[0][0]=1;
for(int i=1;i<=m;i++)
{
    for(int j=0;j<=i;j++)
    {
        if(j==0)
        {
            dp[i][j]=dp[i-1][j]*(1-p[i]);
        }
        else
        {
            dp[i][j]=dp[i-1][j-1]*p[i]+dp[i-1][j]*(1-p[i]);
        }
    }
}

如果求dp[n][j]（k<=j<=n）的和就行了。

#include<bits/stdc++.h>
#define LL long long
using namespace std;

double dp[2005][2005];
double p[2005];
vector<double> v[100005];

int main()
{
    int n, m, k, a;
    double pp;
    scanf("%d%d%d",&n,&m,&k);
    for(int i=0;i<n;i++)
    {
        scanf("%d%lf",&a,&pp);
        v[a].push_back(pp);
    }
    for(int i=1;i<=m;i++)
    {
        double s=1;
        for(int j=0;j<v[i].size();j++)
        {
            s*=(1-v[i][j]);
        }
        p[i]=1.0-(s);
    }
    memset(dp, 0, sizeof(dp));
    dp[0][0]=1;
    for(int i=1;i<=m;i++)
    {
        for(int j=0;j<=i;j++)
        {
            if(j==0)
            {
                dp[i][j]=dp[i-1][j]*(1-p[i]);
            }
            else
            {
                dp[i][j]=dp[i-1][j-1]*p[i]+dp[i-1][j]*(1-p[i]);
            }
        }
    }
    double ans=0;
    for(int i=k;i<=m;i++)
    {
        ans+=dp[m][i];
    }
    printf("%.3f\n",ans);

    return 0;
}