半素数：区间筛+唯一分解定理

最新推荐文章于 2025-07-10 10:51:09 发布

原创最新推荐文章于 2025-07-10 10:51:09 发布 · 1.3k 阅读

5 ·

CC 4.0 BY-SA版权

数论专栏收录该内容

17 篇文章

订阅专栏

本文详细解析了半素数的概念及其筛选方法，通过埃氏筛法原理，阐述了如何在指定区间内高效筛选出半素数。文章深入讨论了唯一分解定理的应用，以及如何结合区间筛法实现半素数的有效识别。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目链接：https://ac.nowcoder.com/acm/contest/637/C
题目大意：
在这里插入图片描述

首先我们要知道什么是唯一分解定理：
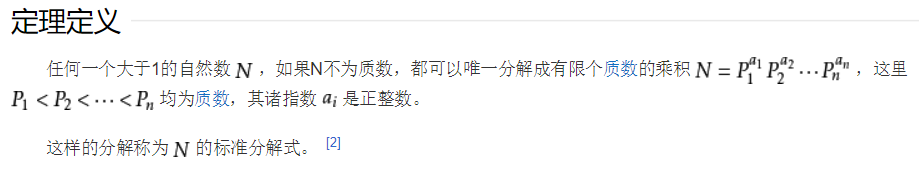
在这里插入图片描述
所以可以由唯一分解定理可以推出：

推论一：若一个数可以进行因数分解，则得到的两个数一定是有一个>=sqrt(x),另一个<=sqrt(x).

推论二：若一个数可以进行素因数分解：分解成(P1^a1) * (P2^a2) * (P2^a2)。

(1)如果Pi中有并且只有一个素因数>sprt(n),那么它的幂一定为1。如果为2那么P ^2 > n 显然是不可能存在的。

(2)还有一种可能就是没有>sprt(n)素因数。但是此时，除非P1=sqrt(n)，不然n的素因数一定>2，因为2个<sqrt(n)的乘积不可能==n。

所以我们确定半素数的分解形式：p^2或者p*q并且p<sqrt(n)，q>sqrt(n)。

然后我们要知道什么是埃氏筛：

介绍：埃拉托斯特尼筛法，利用当前已经找到的素数，从后面的数中筛去当前素数的倍数，由预备知识一可知，当前素数已经是筛去数的质因子，如此下去能筛除所有之后的合数，是一种比较快的筛法，O(nloglogn) 。

区间筛法：利用埃氏筛的思想，求区间[L, R]的素数，可以打出[2, 根号®]的素数，然后筛出区间[L, R]的合数，由推论一可以知道：[L, R]的合数其中有一个素数<=sqrt(x)。所以一定能够筛掉合数。

进入正题：
我们首先筛出[L, R]中每一个X只有一个素因数<=sqrt(X)的数，利用区间筛的思想，一个数只能有一个<=sqrt(X)的素因数。如果被<=sqrt(X)的素因数标记两次，那么这个数就一定不是半素数（一个素因数只会标记一次）。

memset(vis, 0, sizeof(vis));
for(int i=0;i<tot&&prime[i]*prime[i]<=R;i++)
{
    LL u=prime[i];
    LL v=max(u*u, L);//因为要对于一个因数u，我们只能筛满足u<=sqrt(v)的所有v，所以v>=u*u
    for(LL j=(v+(u-v%u)%u);j<=R;j+=u)//j=区间[v, R]内第一个大等于u的倍数
    {
        if(vis[j-L]==0)
        {
            vis[j-L]=u;
        }
        else		//标记两次
        {
            vis[j-L]=-1;
        }
    }
}

现在我们得到了区间[L, R]只有一个素因数<=sqrt(X)的数。
我们就要判断它是不是p*q或者p^2。

根据唯一分解定理：
如果一个只有一个素因数<=sqrt(X)的数p。
那么他的分解形式：q>sqrt(X)
(p^k1)*(q^k2)。根据推论二（1）可以找到k2==0或者1。

所以半素数满足半素数的只有
（1）k1=2	k2=0：	p^2
（2）k1=1	k2=1:	p*q

for(LL i=L;i<=R;i++)
    {
        if(vis[i-L]>0)
        {
            LL x=i/vis[i-L];//假设p=vis[i-L]
            if(x==vis[i-L]||x%vis[i-L])//如果x==vis[i-L];那么是p^2
            //如果是p^k*q并且k>2，那么x=p^(k-1)*q一定是p的倍数。x%vis[i-L]==turn，那么说明：k==1。那么是：p*q。这样所有的半素数就筛出来了。
            {
                v.push_back(vis[i-L]);
                v.push_back(x);
            }
        }
    }

全部代码：

#include <bits/stdc++.h>
using namespace std;
#define LL long long
const int maxn=100001;
LL vis[maxn];
int tot=0;
int prime[maxn];

void PRI()
{
    memset(vis, 0, sizeof(vis));
    for(int i=2;i<maxn;i++)
    {
        if(!vis[i])
        {
            prime[tot++]=i;
        }
        for(int j=0;j<tot&&i*prime[j]<maxn;j++)
        {
            vis[i*prime[j]]=1;
            if(i%prime[j]==0)
            {
                break;
            }
        }
    }
}

vector<LL> v;

void dfs(LL L, LL R)
{
    memset(vis, 0, sizeof(vis));
    for(int i=0;i<tot&&prime[i]*prime[i]<=R;i++)
    {
        LL u=prime[i];
        LL v=max(u*u, L);
        for(LL j=(v+(u-v%u)%u);j<=R;j+=u)
        {
            if(vis[j-L]==0)
            {
                vis[j-L]=u;
            }
            else
            {
                vis[j-L]=-1;
            }
        }
    }
    for(LL i=L;i<=R;i++)
    {
        if(vis[i-L]>0)
        {
            LL x=i/vis[i-L];
            if(x==vis[i-L]||x%vis[i-L])
            {
                v.push_back(vis[i-L]);
                v.push_back(x);
            }
        }
    }
}

int main()
{
    PRI();
    LL L, R;
    cin>>L>>R;
    dfs(L, R);
    printf("%d\n",v.size()/2);
    for(int i=0;i<v.size();i+=2)
    {
        printf("%lld %lld %lld\n",v[i]*v[i+1],v[i],v[i+1]);
    }

    return 0;
}