代码随想录算法训练营第十六天|104.二叉树的最大深度| 111.二叉树的最小深度|222.完全二叉树的节点个数

什么是深度，什么是高度，如何求深度，如何求高度？

• 高度和深度是相反的表示，深度是从上到下数的，而高度是从下往上数。
• 深度是二叉树中任意一个结点到根结点之间的距离。
• 树的深度和高度是相等的，而对其他节点来说深度和高度不一定相等。
• 求高度用后序遍历；求深度用前序遍历

104.二叉树的最大深度

题目：给定一个二叉树 root ，返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

C#递归算法：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    public int MaxDepth(TreeNode root)
    {
       if (root == null) {
            return 0;
        }
        return Math.Max(MaxDepth(root.left), MaxDepth(root.right)) + 1;
    }
}

---

111. 二叉树的最小深度

题目：给定一个二叉树，找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明：叶子节点是指没有子节点的节点。
示例一：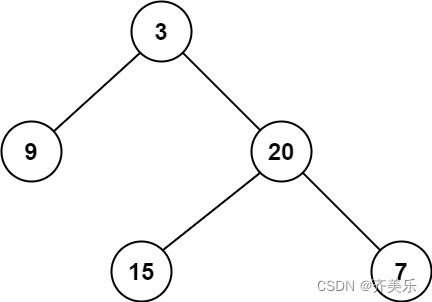

输入：root = [3,9,20,null,null,15,7]
输出：2

思路：最小深度等于最小高度，可以使用后续递归遍历。
C#递归代码：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    // 确定递归参数和返回值
    public int MinDepth(TreeNode root) {
        //确定递归终止条件
        if(root == null) return 0;
        //左子树处理
        int leftHeight = MinDepth(root.left);
        //右子树处理
        int rightHeight = MinDepth(root.right);
        //中间结点处理
        if(root.left == null) return 1+rightHeight;
        if(root.right == null) return 1+leftHeight;
        // 左右结点都不为null
        return 1+Math.Min(leftHeight,rightHeight);
    }
}

---

222. 完全二叉树的节点个数

题目：给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。
示例 1：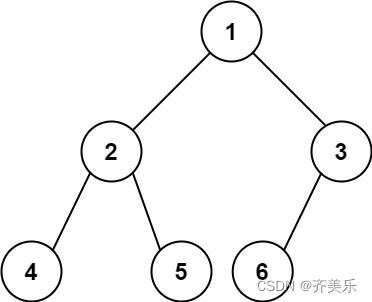

输入：root = [1,2,3,4,5,6]
输出：6

思路一：暴力解法，迭代法层序遍历，遇到一个元素就加一。
思路二：暴力解法，递归遍历。
思路三：完全二叉树只有两种情况，情况一：就是满二叉树，情况二：最后一层叶子节点没有满。

• 对于情况一，可以直接用2^深度 - 1来计算，注意这里根节点深度为1。
• 对于情况二，分别递归左孩子，和右孩子，递归到某一深度一定会有左孩子或者右孩子为满二叉树，然后依然可以按照情况1来计算。
  完全二叉树（一）如图：
  

C#代码，思路一：

public class Solution {
    public int CountNodes(TreeNode root) {
        int result = 0;
        if(root == null) return result;
        var queue = new Queue<TreeNode>();
        queue.Enqueue(root);
        while(queue.Any())
        {
            int len = queue.Count;
            while(len > 0)
            {
                result++;
                var node = queue.Dequeue();
                if(node.left!=null) queue.Enqueue(node.left);
                if(node.right!= null) queue.Enqueue(node.right);
                len--;
            }
        }
        return result;
    }
}

C#代码，思路二：后序递归遍历

public class Solution {
    public int CountNodes(TreeNode root) {
        if(root == null) return 0;
        int leftCount = CountNodes(root.left);
        int rightCount = CountNodes(root.right);
        return 1+leftCount+rightCount;
    }
}

C#代码，思路三

public class Solution {
    public int CountNodes(TreeNode root) {
        if(root == null) return 0;
        //利用完全二叉树性质
        var curLeft = root.left;
        var curRight = root.right;
        int leftDepth = 0;
        int rigthDepth = 0;
        while(curLeft != null)
        {
            curLeft = curLeft.left;
            leftDepth++;
        }
        while(curRight != null)
        {
            curRight = curRight.right;
            rigthDepth++;
        }
        if(leftDepth == rigthDepth) return (2<<leftDepth) - 1;
        //左
        int leftCount = CountNodes(root.left);
        //右
        int rightCount = CountNodes(root.right);
        //中
        return 1+leftCount+rightCount;
    }
}