常见动态规划问题分析与代码

动态规划（Dynamic Programming，简称DP），虽然抽象后进行求解的思路并不复杂，但具体的形式千差万别，找出问题的子结构以及通过子结构重新构造最优解的过程很难统一。
本文主要是对一些常见的动态规划题目的收集。

动态规划求解的一般思路

动态规划求解的一般思路：
判断问题的子结构（也可看作状态），当具有最优子结构时，动态规划可能适用。
求解重叠子问题。一个递归算法不断地调用同一问题，递归可以转化为查表从而利用子问题的解。分治法则不同，每次递归都产生新的问题。
重新构造一个最优解。

备忘录法

动态规划的一种变形，使用自顶向下的策略，更像递归算法。
初始化时表中填入一个特殊值表示待填入，当递归算法第一次遇到一个子问题时，计算并填表；以后每次遇到时只需返回以前填入的值。

1.硬币找零

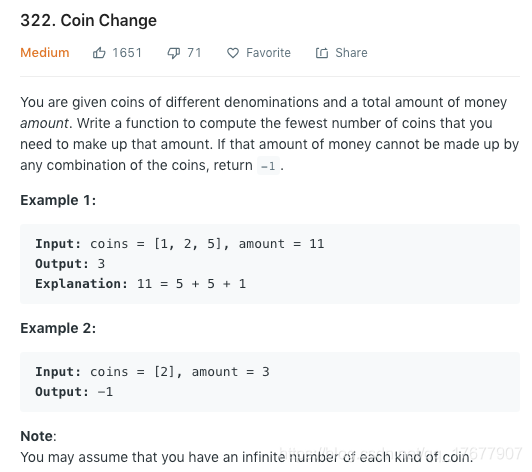
给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1。

思路

代码

2.字符串相似度/编辑距离（edit distance）

3.最长公共子序列(Longest Common Subsequence,lcs)

扩展1：输出所有lcs

扩展2：通过LCS获得最长递增自子序列

4.最长递增子序列（Longest Increasing Subsequence,lis）

扩展：求解lis的加速

5.最大连续子序列和/积