详解SVM系列（四）：线性支持向量机与软间隔最大化

线性支持向量机

线性可分问题的支持向量机学习方法，对线性不可分训练数据是不适用的，因为这时上述方法的不等式约束并不能都成立。
举2个例子：

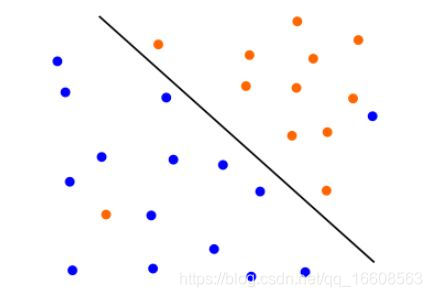
如果没有混入异常点，导致不能线性可分，则数据可以按上面的实线来做超平面分离的。

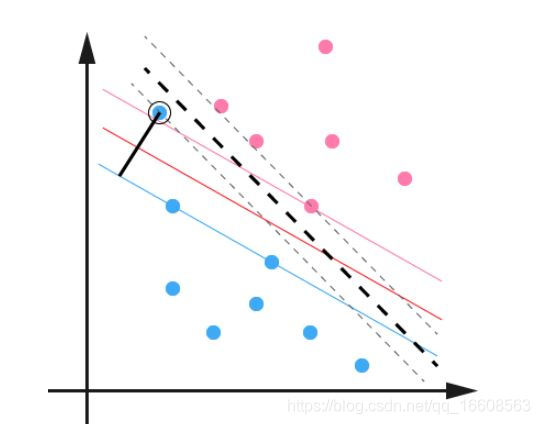
这种情况虽然不是不可分的，但是由于其中的一个蓝色点不满足线性可分支持向量机中的不等式约束，导致模型的泛化效果很差。
正常情况下（没有那个蓝色异常点）分离超平面应该是红色的那条线，由于异常点的存在，实际得到的分离超平面是黑色的粗虚线。（间隔不同啊，所以泛化性能也不一样）

软间隔最大化

怎么解决呢？
对硬间隔最大化做出一些让步：放宽SVM的限制，可以允许存在一些误分类的点。
线性不可分意味着某些样本点$(x_i,y_i)$不能满足函数间隔大于等于1的约束条件，为了解决这个问题，可以对每个样本点$(x_i,y_i)$引进一个松弛变量${\zeta }_i\ge 0$,使得函数间隔加上松弛变量大于等于1.这样约束条件变为
$y_i(w{x}_i+b)\ge 1-{\zeta }_i$
松弛变量的引入就是i为了对付那些离群点的，其他点（姑且称作正常点）的松弛变量都是0
同时，对每一个松弛变量${\zeta }_i$，支付一个代价${\zeta }_i$。目标函数由原来的$\frac{||w|{|}^2}{2}$变成
$\frac{||w|{|}^2}{2}+C\sum _{i=1}^N{\zeta }_i$ -------------------------（式1）
这里,C称为惩罚参数，一般由应用问题决定。
C值大的时候对误分类的惩罚大，这时候间隔会变小
C值小时对误分类的惩罚变小，间隔相应的变大。

式1的意义在于使间隔尽量大，同时使误分类的个数尽量少。
线性不可分的线性支持向量机的学习问题变成下面的凸二次规划问题：
${min}_{w,b,\zeta }\frac{||w|{|}^2}{2}+C\sum _{i=1}^N{\zeta }_i$ -----------------------------(式2)
$s.t:y_i(w{x}_i+b)\ge 1-{\zeta }_i$