深度学习：ResNet：Deep Residual for Image Recognition

1 abstract

将层改为residual functions，模型更容易优化

模型越深越好，是VGG的8倍。模型复杂度比VGG更低

是2015年ImageNet 的1st

深度是获胜的关键

2 indroduction

模型的深度丰富了模型的features

深模型的问题：梯度消失或爆炸，难找到最优值，现有方案：normalized initlalization ,intermediate

更深： 精度无法进一步提高，损失值比浅层更大

3 解决： 优化F(X) 比优化F(x) +x 的难度更高

+x的部分：

identify function

跳跃一层或者多层layers

不增加parameters

不增加复杂度计算

容易实现

让损失值和预测精度都随着深度更好。

总共152层，复杂程度比VGG更低。

3.1 多层layers=H(x),约等于a residual function==F(x)=H(x)-x=F(x）+x

 

3.2 identity maping by shortcut

shortcut block的流程：y=F(x,{wi})+x, 其中

plain block  没有x，在深度，参数，成本没有差别

pooling 的因素会改变input，output的维数，用Ws 来补齐x 需要的维度

F(x,{w}) 中的layer 可以是FC，也可以是Conv layers

3.3  network 结构

普通版：大量连续相同的conv layer，input和output 的shape 相同，当feature map 减半，filter 的数量就翻倍。普通版的filter 更少，计算复杂度更低，运算量更少(VGG 18%)

Resnet: 增加了 shortcout connection，维度不同的时候用Ws 补齐（padding with Zeros）1*1 的convolution

3.4 代码实现：

数据处理： rescale： 最短边从S=randomized[256,480] 之间抽样，得到更多的图； 224*224 修剪； 翻转；所有样本的像素减去均值； 标准颜色扩充处理。

conv layer： BN 激活

sgd,lr=0.1 ,当error 不降的时候，降10倍，60万iteration，weight decay =0.0001 momentum =0.9，没有drouout

4.1 ImageNet classification

plain network ：

x2 是代表2个block

stride=2 让模型缩小一半

BN 避免了梯度小时，也没有影响预测精度，但是深模型的training error 很高。可能是很低的convergence rate 造成的，

RseNet： ResNet converge faster 在反向传递中产生效果，zero padding

Bottleneck 的设计目的： 加速计算；1*1 conv ，3*3 conv，1*1 conv；先缩小，再放大还原；相比于两个3*3 的conv 并没有增加计算量，bottleneck +identity short cut 很完美；

50层的layer ResNet ：

换成了bottleneck block

101 和152 的layer： 增加了bottleneck block 的数量，复杂性大幅度低于VGG16-19.没有degradation。预测精度大幅度提高，

 

5 why Resnet works

梯度消失或爆炸导致反向传递的时候很难更新

Resnet 梯度消失时，返回自己，可以进行参数更新。相同颜色的shape一致。

参考： https://www.bilibili.com/video/av16274698

https://www.bilibili.com/video/av16275481

https://www.bilibili.com/video/av16284825

https://www.bilibili.com/video/av16186719?from=search&seid=11680144772516069001

问题1： ResNet 好在哪里？

https://www.zhihu.com/question/52375139

1 使网络更容易在某些层学到恒等变换(identity mapping) 。在某些层执行恒等变换是一种构造性解，使更深的模型的性能至少不低于较浅的模型。

2 残差网络是很多浅层网络的集成，层数的指数级那么多，主要的实验证据是：把Resnet 中某些层直接删掉，模型的性能几乎不下降。

3 残差网络使信息更容易在各层之间流动，包括在前向传播时提供特征重用，在反向传播时缓解梯度信号消失。

q2 ：Batch normalization 先归一化然后恢复有何意义

前一层参数的改变导致后一层数据分布的改变称为 Internal covariate shift，用BN 解决：在网络的每一层输入的时候，又插入了一次归一化层，

但是会影响到本层网络A 所学到的特征，比如网络中间某一层学习到特征本身就分布在S型型激活函数的两侧，你强制把它归一化处理，标准化也限制在了1，把数据变换成了分布于S 函数的中间部分，这就相当于学习到的特征分布被搞坏了，那么就要做变换重构，引入可学习的参数γ、β，这就是算法。

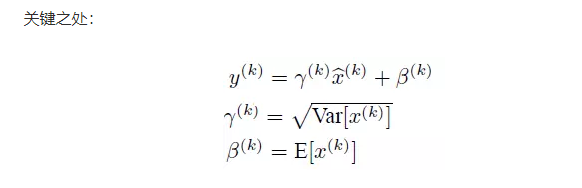
通过学习到的重构参数，可以恢复出原始的某一层所学到的特征的。

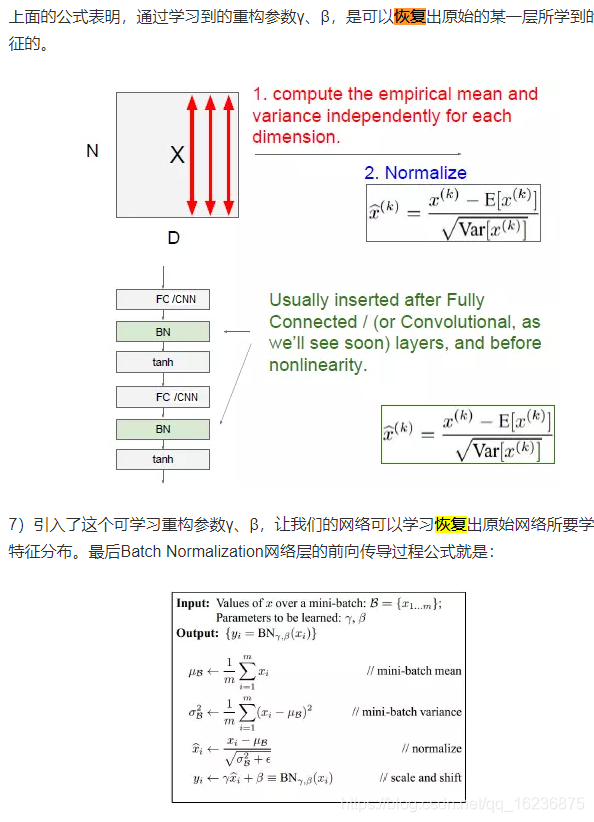
BN 层是对每个神经元做归一化处理，甚至只需要对某个神经元进行归一化，而不是对一整层网络的神经元进行归一化，既然BN 是对单个神经元的运算，那么在CNN 中，假如某一层卷积层有6个特征图，每个特征图的大小是100*100，这就相当于这一层网络有6*100*100 个神经元，如果采用BN，就会有6*100*100个参数γ、β。因此CNN 上BN的使用，就是使用了类似权重共享的策略，把一整张特征图当作一个神经元来处理。

https://www.jianshu.com/p/05f3e7ddf1e1