本文介绍了逻辑回归模型，它是一种预测值限定在[0,1]之间的回归模型，常用于分类问题。逻辑回归通过逻辑方程限制预测概率，并采用最大似然估计作为目标函数。损失函数通常取负对数似然，优化方法包括梯度下降，如批量梯度下降（BGD）、随机梯度下降（SGD）和小批量梯度下降（MBGD）。"
109344516,9500662,复消色差透镜设计与优化,"['光学设计', '光学感测', '复消色差', '玻璃特性']
逻辑回归模型
- 回归即 y = f ( x ) y=f(x) y=f(x)表明自变量与因变量的关系
- 最简单的回归是线性回归 h θ ( x ) = θ T x h_\theta(x)=\theta^Tx hθ(x)=θTx
- 缺点:对异常值敏感，主要是由于线性回归在整个实数域内敏感度一致，而分类范围，需要在[0,1]
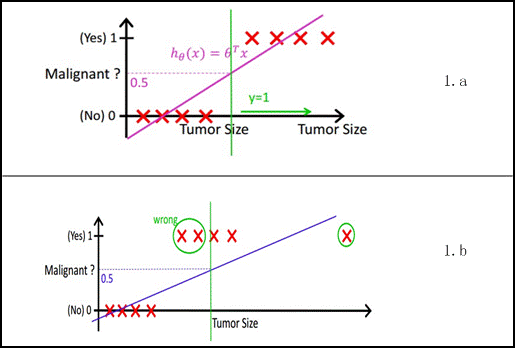
- 逻辑回归：将预测值限定为[0,1]间的一种回归模型
- 逻辑曲线在z=0时，十分敏感，在z>>0或z<<0处，都不敏感，将预测值限定为(0,1)。
- 逻辑方程： g ( z ) = 1 1 + e − z g(z)=\frac{1}{1+e^{-z}} g(z)=1+e−z1
- 逻辑回归模型： h θ ( x ) = 1 1 + e − θ T x ∈ [ 0 , 1 ] h_\theta(x)=\frac{1}{1+e^{-\theta^Tx}}\in[0,1] hθ(x)=1+e−θTx1∈[0,1]，可理解为预测为1的概率
- 目标函数：最大化似然概率
m a x L ( θ ) = m a x ∏ i = 1 m p ( y i ∣ x i , θ ) T w o C l a s s i f y : p ( y i ∣ x i , θ ) = p 1 = p ( y = 1 ∣ x , θ ) = h θ ( x ) p 0 = p ( y = 0 ∣ x , θ ) = 1 − h θ ( x ) = h θ ( x ) y i ( 1 − h θ ( x ) ) 1 − y i maxL(\theta)=max\prod_{i=1}^{m}p(y_i|x_i,\theta) \\ TwoClassify:p(y_i|x_i,\theta)=\frac{p_1 = p(y=1|x,\theta) = h_\theta(x)}{p_0 = p(y=0|x,\theta) = 1 - h_\theta(x)}=h_\theta(x)^{y_i}(1-h_\theta(x))^{1-y_i} maxL(θ)=maxi=1∏mp(yi
最低0.47元/天 解锁文章
扫一扫
1108
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
