Huffman Tree——文件压缩

最新推荐文章于 2022-08-24 20:25:30 发布

青云衣兮白霓裳

最新推荐文章于 2022-08-24 20:25:30 发布

阅读量590

点赞数

CC 4.0 BY-SA版权

分类专栏： C++ 文章标签：文件压缩 Huffman 堆解压缩

本文链接：https://blog.youkuaiyun.com/qq_15000103/article/details/79723004

本文介绍了Huffman树的压缩和解压缩原理，并通过代码实现展示了其在文件压缩中的实战应用，尤其是在文本文件上的操作。然而，该方法目前不适用于图片和音频文件的压缩与解压缩。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1 Huffman树的压缩和解压缩原理

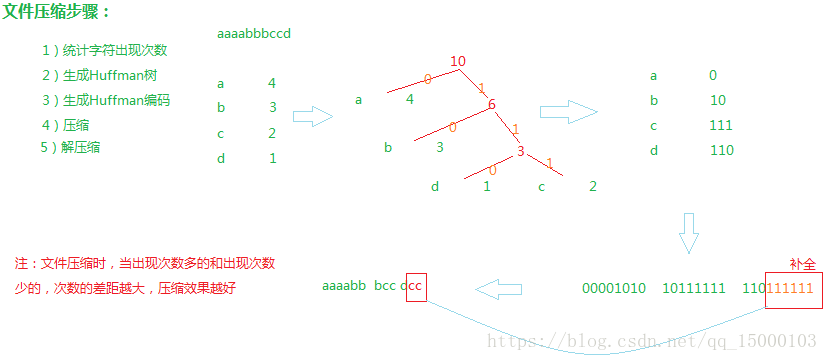
这里写图片描述
2 文件压缩（Huffman树的实战应用）
* 代码实现*

//Heap.h
#pragma once
#include <iostream>
#include<string>
#include<vector>
#include"assert.h"
using namespace std;

template<class T, class Compare>
class Heap
{
public:
    Heap()
        :_a(0)
    {   }

    //建堆  
    Heap(T* a, int sz)
    {
        _a.resize(sz);
        int i = 0;
        for (i = 0; i < sz; i++)
        {
            _a[i] = a[i];
        }
        for (i = (_a.size() - 2) / 2; i >= 0; i--)//外层循环，每次传入根结点下标。（_a.size()-2）/2即为最后一个非叶子结点下标。  
        {
            AdjustDown(i);
        }
    }

    void AdjustDown(int root)//向下调整
    {
        Compare com;
        int parent = root;
        int child = parent * 2 + 1;
        while (child < _a.size())
        {
            if (child + 1 < _a.size()
                && com(_a[child + 1], _a[child]))//比较孩子
            {
                ++child;
            }
            if (com(_a[child], _a[parent]))
            {
                swap(_a[child], _a[parent]);
                parent = child;
                child = parent * 2 + 1;
            }
            else   //表示父亲大于孩子
            {
                break;
            }
        }
    }
    void AdjustUp(int child)//向上调整
    {
        Compare com;
        int parent = (child - 1) / 2;
        while (child > 0)//这里的parent不可能为负数
        {
            //if (_a[child]>_a[parent])
            if (com(_a[child], _a[parent]))
            {
                swap(_a[child], _a[parent]);
                child = parent;
                parent = (child - 1) / 2;
            }
            else
            {
                break;
            }
        }
    }
    void Push(const T&x)
    {
        _a.push_back(x);
        AdjustUp(_a.size() - 1);
    }
    void Pop()
    {
        assert(!_a.empty());
        swap(_a[0], _a[_a.size() - 1]);
        _a.pop_back();
        AdjustDown(0);
    }

    const T&Top()
    {
        return _a[0];
    }

    size_t Size()
    {
        return _a.size();
    }
private:
    vector<T> _a;//层序存储
};
template<class T>