题目要求
1.按要求完成下面的各项需求。
已知有一个苹果的数据集,保存在apple.txt文件中,t1是含糖量,t2是含水量,y标签表示苹果的好坏:1表示好,0表示不好
利用支持向量机模型,完成以下要求:
完成数据集的加载、初始化,洗牌,将数据集合理分割成训练集和测试集
实现调用库函数进行分类
分别求出训练集和测试集的准确率
画出整个样本数据并画出分界线
(二)评分要求
1.完成数据集的加载和初始化(8分)
2.将数据集洗牌(6分),合理分割成训练集和测试集(6分)
3.正确调用SVM库函数并训练模型(30分)
4.分别求出训练集和测试集的准确率(20分)
5.画出整个样本数据并画出分界线(30分)
数据准备
0.697,0.46,1
0.774,0.376,1
0.634,0.264,1
0.608,0.318,1
0.556,0.215,1
0.403,0.237,1
0.481,0.149,1
0.437,0.211,1
0.666,0.091,0
0.243,0.267,0
0.245,0.057,0
0.343,0.099,0
0.639,0.161,0
0.657,0.198,0
0.36,0.37,0
0.593,0.042,0
0.719,0.103,0
题目总结
对于调库实现svm的SVC分类器来说,其实是很简单的,重点在于对数据的前期处理。
这里需要注意的是,直接调库使用的数据,标签值不需要转成列向量,训练值也不需要拼接x0=1那一列,将特征值数据和标签值直接传入就好。
另一个重点在于画图。需要画出等高线,还需要画出等值面,这些需要一些前期准备,比如画布范围的选择,均等值的划分,点到判定边界距离的求解,等。画起来比较繁琐,需要多加练习。
代码及注释如下:
import numpy as np
from matplotlib import pyplot as plt
from sklearn.svm import SVC
# 设置中文字体和负号正确显示
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 读取数据
data = np.loadtxt(r'smt.txt',delimiter=',')
# 定义数据处理函数
def preprocess(data):
# 数据提取
X = data[:,:-1]
y = data[:,-1]
# 特征缩放
X -= np.mean(X,axis=0)
X /= np.std(X,axis=0,ddof=1)
# 数据初始化
m = len(X)
X = np.c_[X]
y = np.c_[y]
# 洗牌
np.random.seed(3)
o = np.random.permutation(m)
X = X[o]
y = y[o]
# 数据切割
d = int(0.7 * m)
X_train,X_test = np.split(X,[d])
y_train,y_test = np.split(y,[d])
return X,y.ravel(),X_train,X_test,y_train.ravel(),y_test.ravel()
# 调用数据处理函数获得处理好的数据
X,y,X_train,X_test,y_train,y_test = preprocess(data)
# 创建svm模型
model = SVC(C=5,kernel='rbf')
# 跑数据
model.fit(X_train,y_train)
# 4.分别求出训练集和测试集的准确率(20分)
print('训练集的准确率是:',model.score(X_train,y_train))
print('测试集的准确率是:',model.score(X_test,y_test))
# 5.画出整个样本数据并画出分界线(30分)
# 画图部分
# 首先确定画布范围
x1_min,x1_max = np.min(X[:,0]),np.max(X[:,0])
x2_min,x2_max = np.min(X[:,1]),np.max(X[:,1])
# 将画布切分成200*200
x1,x2 = np.mgrid[x1_min:x1_max:200j,x2_min:x2_max:200j]
# 拼成坐标
x1x2 = np.c_[x1.ravel(),x2.ravel()]
z = model.decision_function(x1x2)
z = z.reshape(x1.shape)
# 画散点
plt.scatter(X[:,0],X[:,1],zorder=10,c=y)
plt.scatter(X_test[:,0],X_test[:,1],edgecolors='k',facecolor='none',s=100)
# 画面
plt.contourf(x1,x2,z>=0,cmap=plt.cm.Paired)
# 画线
plt.contour(x1,x2,z,levels=[-1,0,1])
plt.show()
关于核函数的选择
对于这组数据,由于数据较少,所以刚开始选择的是线性核,但是在调试各种参数以后,模型表现的并不好,所以此时要考虑换一个核函数试一下。
最终我选定了‘rbf’核函数,表现很好。
总结,对于不同的数据,在数据处理好的情况下,先从简单的模型选起,简单总比复杂好,但是,模型过于简单,数据拟合程度较差,应该逐步加大模型的复杂程度。
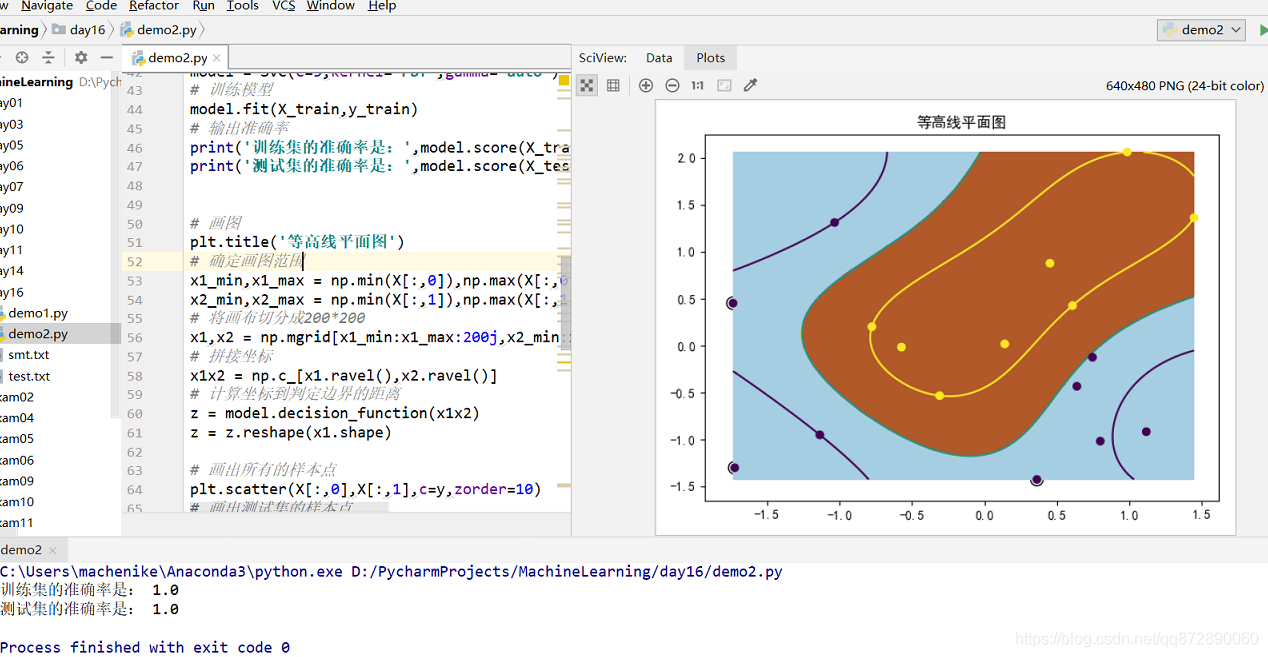





 本文探讨了在机器学习中使用支持向量机(SVM)进行分类时的模型选择和训练过程。重点在于数据的前期处理,如不需要转换标签列向量和添加x0列。在画图方面,强调了等高线和等值面的绘制。通过实践,发现线性核对数据拟合不足,改用'rbf'核函数后效果显著提升。总结经验,应根据数据逐步调整模型复杂度。
本文探讨了在机器学习中使用支持向量机(SVM)进行分类时的模型选择和训练过程。重点在于数据的前期处理,如不需要转换标签列向量和添加x0列。在画图方面,强调了等高线和等值面的绘制。通过实践,发现线性核对数据拟合不足,改用'rbf'核函数后效果显著提升。总结经验,应根据数据逐步调整模型复杂度。
















 651
651

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








