cf519F(二分答案+莫比乌斯反演+线性容斥)

最新推荐文章于 2023-05-15 21:22:33 发布

qkoqhh

最新推荐文章于 2023-05-15 21:22:33 发布

阅读量453

点赞数

分类专栏：二分数论

本文链接：https://blog.youkuaiyun.com/qkoqhh/article/details/83515421

版权

数论同时被 2 个专栏收录

35 篇文章

订阅专栏

二分

14 篇文章

订阅专栏

题意：从一个序列中的最小互斥序列（即所有数的gcd为1）的长度

这个一看就是比较套路的题，还是有不少地方得学的。。

然后显然需要二分答案，考虑选取长度为k的序列的gcd，设gcd为d的选取方案为f(d)，然而f(d)并不好求

而如果设选取的gcd为d的倍数的方案数为g(d)，那么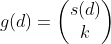 $g(d)=\begin{pmatrix} s(d)\\ k \end{pmatrix}$ ，其中s(d)为原序列中能被d整除的个数，这个可以直接对每个数分解因子得到。。（这个思路其实和https://blog.youkuaiyun.com/qkoqhh/article/details/82227846比较类似

然后g求出来之后就能求f了，因为

$g(d)=\sum_{d|k}f(k)$

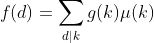
$f(d)=\sum_{d|k}g(k)\mu (k)$

而只需要判断f(1)是否大于0就能够二分check了。。

复杂度O(nsqrt(n)+nlogn)

/**
 *　　　　　　　　┏┓　　 　┏┓
 * 　　　　　　　┏┛┗━━━━━━━┛┗━━━┓
 * 　　　　　　　┃　　　　　　　┃ 　
 * 　　　　　　　┃　　　━　　 　┃
 * 　　　　　　　┃　＞　　　＜　┃
 * 　　　　　　　┃　　　　　　　┃
 * 　　　　　　　┃...　⌒　... 　┃
 * 　　　　　　　┃　　　　　　　┃
 * 　　　　　　　┗━┓　　　┏━┛
 * 　　　　　　　　　┃　　　┃　Code is far away from bug with the animal protecting　　　　　　　　　　
 * 　　　　　　　　　┃　　　┃   神兽保佑,代码无bug
 * 　　　　　　　　　┃　　　┃　　　　　　　　　　　
 * 　　　　　　　　　┃　　　┃  　　　　　　
 * 　　　　　　　　　┃　　　┃
 * 　　　　　　　　　┃　　　┃　　　　　　　　　　　
 * 　　　　　　　　　┃　　　┗━━━┓
 * 　　　　　　　　　┃　　　　　　　┣┓
 * 　　　　　　　　　┃　　　　　　　┏┛
 * 　　　　　　　　　┗┓┓┏━┳┓┏┛
 * 　　　　　　　　　　┃┫┫　┃┫┫
 * 　　　　　　　　　　┗┻┛　┗┻┛
 */
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<queue>
#include<cmath>
#include<map>
#include<stack>
#include<set>
#include<bitset>
#define inc(i,l,r) for(int i=l;i<=r;i++)
#define dec(i,l,r) for(int i=l;i>=r;i--)
#define link(x) for(edge *j=h[x];j;j=j->next)
#define mem(a) memset(a,0,sizeof(a))
#define ll long long
#define eps 1e-8
#define succ(x) (1LL<<(x))
#define lowbit(x) (x&(-x))
#define sqr(x) ((x)*(x))
#define mid ((x+y)/2)
#define NM 300005
#define nm 100005
#define pi 3.1415926535897931
using namespace std;
const ll inf=1e9+7;
ll read(){
    ll x=0,f=1;char ch=getchar();
    while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
    while(isdigit(ch))x=x*10+ch-'0',ch=getchar();
    return f*x;
}





int n,m,ans,_x,s[NM],mu[NM],tot,prime[NM];
ll p[NM],inv[NM],invp[NM],g[NM];
bool v[NM];


void init(){
    m=3e5;p[1]=inv[1]=invp[1]=p[0]=invp[0]=1;
    inc(i,2,m)p[i]=p[i-1]*i%inf,inv[i]=inv[inf%i]*(inf-inf/i)%inf,invp[i]=invp[i-1]*inv[i]%inf;
    mu[1]=1;
    inc(i,2,m){
	if(!v[i])prime[++tot]=i,mu[i]=-1;
	inc(j,1,tot){
	    if(i*prime[j]>m)break;
	    v[i*prime[j]]++;
	    if(i%prime[j]==0)mu[i*prime[j]]=0;else mu[i*prime[j]]=-mu[i];
	}
    }
}

ll check(int t){
    ll k=0;
    inc(i,1,m)if(s[i]>=t)g[i]=p[s[i]]*invp[t]%inf*invp[s[i]-t]%inf;else g[i]=0;
    inc(i,1,m)k+=g[i]*mu[i],k%=inf;
    return k;
}

int main(){
    init();
    n=read();
    inc(i,1,n){
	_x=read();
	for(int j=1;sqr(j)<=_x;j++)if(_x%j==0){
	    s[j]++;if(sqr(j)<_x)s[_x/j]++;
	}
    }
    ans=-1;
    for(int x=1,y=n;x<=y;)
	if(check(mid))ans=mid,y=mid-1;else x=mid+1;
    return 0*printf("%d\n",ans);
}

F. Make It One

time limit per test

3 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Janusz is a businessman. He owns a company "Januszex", which produces games for teenagers. Last hit of Januszex was a cool one-person game "Make it one". The player is given a sequence of n

integers ai

It is allowed to select any subset of them, and the score is equal to the greatest common divisor of selected elements. The goal is to take as little elements as it is possible, getting the score 1

. Now Janusz wonders, for given sequence, how much elements should the player choose?

Input

The first line contains an only integer n

(1≤n≤300000

) — the number of integers in the sequence.

The second line contains n

integers a1,a2,…,an (1≤ai≤300000

Output

If there is no subset of the given sequence with gcd equal to 1

, output -1.

Otherwise, output exactly one integer — the size of the smallest subset with gcd equal to 1

Examples