七种距离度量全解析：从氏到汉明，算法选得好，模型搓澡不费脑！

原创于 2025-06-09 10:13:41 发布 · 812 阅读

24 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #人工智能 #欧式距离 #曼哈顿距离 #机器学习 #切比雪夫距离 #汉明距离

大家好！今天我们来聊聊机器学习中的"距离"——不是你和女神的距离，而是数据点之间的数学距离！这些距离度量就像不同性格的朋友，有的直来直去，有的拐弯抹角，有的甚至自带"滤镜"。准备好你的计算器，让我们一起开启这场"距离社交"之旅吧！😎

📐 1. 欧氏距离 (Euclidean Distance) - 直男式距离

定义：两点之间的直线距离，就像你问路时得到的"直走500米右转"的回答。

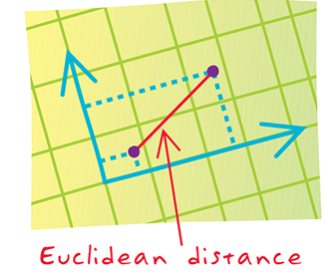
公式：

（简单来说，就是先平方，再求和，最后开根号）

举个栗子🌰：
二维点 A(1,2) 和 B(4,6) 的距离：

特点：

优点：直观易懂，计算简单
缺点：对特征尺度敏感（身高和体重不能直接比）
适合场景：低维空间，特征尺度相近时，KNN聚类、图像相似度计算

比喻：就像直男约会，直奔主题不绕弯子😏

🚦 2. 曼哈顿距离 (Manhattan Distance) - 出租车司机式距离

定义：两点在标准坐标系上的绝对轴距总和。就像在曼哈顿街区要从一个十字路口开车到另一个十字路口，驾驶距离显然不是两点间的直线距离。这个实际驾驶距离就是“曼哈顿距离”。曼哈顿距离也称为“城市街区距离”(City Block distance)。

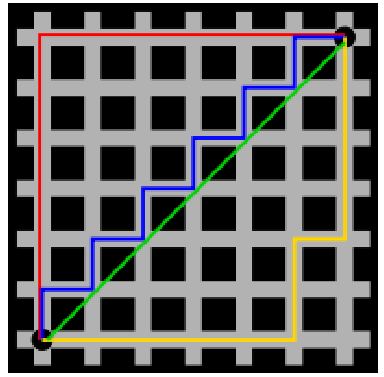
公式：

（简单来说，就是各维度差值的绝对值之和）

举个栗子🌰：
从纽约路口(1,2)到(4,6)：

特点：

优点：计算简单，对异常值不敏感
缺点：忽略了"对角线捷径"
适合场景：高维数据，特征尺度差异大时

比喻：就像出租车司机，只走横平竖直的路🚖

🏰 3. 切比雪夫距离 (Chebyshev Distance) - 国际象棋王式距离

定义：国际象棋中，国王可以直行、横行、斜行，所以国王走一步可以移动到相邻8个方格中的任意一个。这个距离就叫切比雪夫距离。

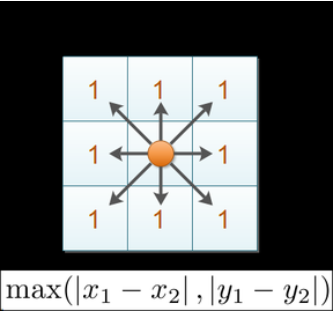
公式：

（简单来说，就是各维度差值的最大值）

举个栗子🌰：
点(1,2)到(4,6)：

特点：

优点：对极端值敏感
缺点：忽略了其他维度的差异
适合场景：棋盘游戏、某些特定优化问题

比喻：就像国际象棋王，只关心最远的那个威胁👑

🌌 4. 闵可夫斯基距离 (Minkowski Distance) - 距离界的变形金刚

定义：是以上欧氏距离、曼哈顿距离、切比雪夫距离的"超级赛亚人"形态，通过参数p控制变形。所以闵氏距离不是一种距离，而是一组距离的定义，是对多个距离度量公式的概括性的表述。

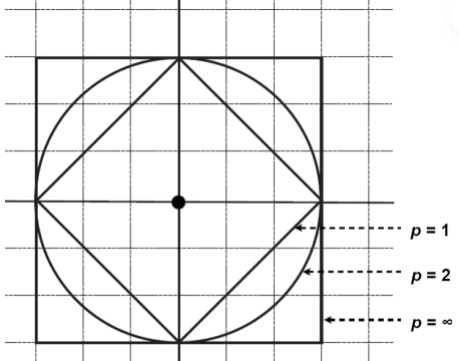
公式：

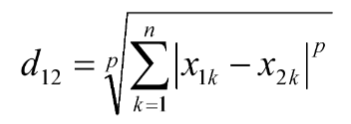
（p=1时为曼哈顿距离，p=2时为欧氏距离，p=∞：切比雪夫距离）

特点：

优点：灵活多变，一统江湖
缺点：需要调参p，可能过拟合
适合场景：需要平衡各维度重要性时

比喻：就像变形金刚，想变啥样变啥样🤖

👗 5. 马氏距离 (Mahalanobis Distance) - 贵族式距离

定义：考虑了数据分布的距离，就像贵族社交圈，不仅看距离，还看"门当户对"。

公式：

（其中Σ是协方差矩阵的逆）

举个栗子🌰：

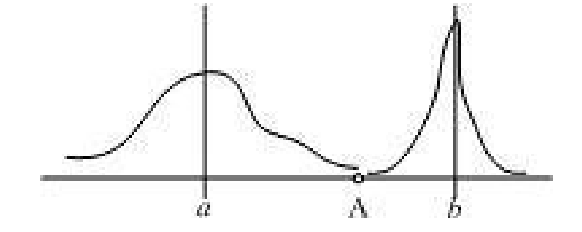
上图有两个正态分布的总体，它们的均值分别为a和b，但方差不一样，则图中的A点离哪个总体更近？或者说A有更大的概率属于谁？

答案是：A离左边的更近，尽管A与b的欧式距离远一些，A属于左边总体的概率更大。

特点：

优点：考虑了特征间的相关性，尺度不变
缺点：计算复杂，需要估计协方差矩阵
适合场景：高维数据，特征相关性强时

比喻：就像贵族社交，不仅看距离，还要看家族背景👑

🧼 6. 标准化欧氏距离 (Standardized Euclidean Distance) - 健身达人式距离

定义：欧氏距离的"健身版"，先对数据进行标准化处理。

公式：

<img src="https://img-blog.csdnimg.cn/20230520123545678.png" />
（其中σ是各维度的标准差）

特点：

优点：解决了欧氏距离的尺度敏感问题
缺点：需要先计算标准差
适合场景：特征尺度差异大时

比喻：就像健身达人，先调整好体型再比距离💪

📡 7. 汉明距离 (Hamming Distance) - 二进制世界的距离

定义：两个等长字符串对应位置的不同字符数目，就像比较两个二进制数的差异。

公式：
<img src="https://img-blog.csdnimg.cn/20230520123556789.png" />
（简单来说，就是对应位置不同的个数）

特点：

优点：计算简单，适合离散数据
缺点：只适用于等长数据
适合场景：编码理论、DNA序列比对

比喻：就像二进制世界的"找不同"游戏🕵️

🎯 距离度量选择指南：如何"撩"到合适的距离？

数据类型：
- 连续型：欧氏/曼哈顿/马氏
- 离散型：汉明
- 混合型：需要特殊处理
特征尺度：
- 尺度相近：欧氏
- 尺度差异大：曼哈顿/标准化欧氏
特征相关性：
- 独立：欧氏/曼哈顿
- 相关：马氏
计算效率：
- 高维数据：曼哈顿/切比雪夫
- 低维数据：欧氏

💻 代码实战：Python中的距离计算

import numpy as np
from scipy.spatial import distance

# 定义两个点
point1 = np.array([1, 2, 3])
point2 = np.array([4, 6, 8])

# 1. 欧氏距离
euclidean_dist = distance.euclidean(point1, point2)
print(f"欧氏距离: {euclidean_dist:.2f}")  # 输出: 7.07

# 2. 曼哈顿距离
manhattan_dist = distance.cityblock(point1, point2)  # cityblock是曼哈顿距离的别名
print(f"曼哈顿距离: {manhattan_dist:.2f}")  # 输出: 11.00

# 3. 切比雪夫距离
chebyshev_dist = distance.chebyshev(point1, point2)
print(f"切比雪夫距离: {chebyshev_dist:.2f}")  # 输出: 5.00

# 4. 闵可夫斯基距离 (p=3)
minkowski_dist = distance.minkowski(point1, point2, p=3)
print(f"闵可夫斯基距离(p=3): {minkowski_dist:.2f}")  # 输出: 6.08

# 5. 标准化欧氏距离
# 先标准化数据
mean = np.mean([point1, point2], axis=0)
std = np.std([point1, point2], axis=0)
std_point1 = (point1 - mean) / std
std_point2 = (point2 - mean) / std
std_euclidean_dist = distance.euclidean(std_point1, std_point2)
print(f"标准化欧氏距离: {std_euclidean_dist:.2f}")

# 6. 汉明距离 (需要转换为二进制字符串)
# 这里简化处理，实际应比较等长二进制串
binary_str1 = '101'
binary_str2 = '110'
hamming_dist = sum(c1 != c2 for c1, c2 in zip(binary_str1, binary_str2))
print(f"汉明距离: {hamming_dist}")  # 输出: 2

📊 距离度量对比表

距离度量	公式特点	计算复杂度	尺度敏感	相关性敏感	适用场景
欧氏距离	平方和开根号	低	是	否	低维，尺度相近
曼哈顿距离	绝对值和	低	否	否	高维，尺度差异大
切比雪夫距离	最大值	低	否	否	棋盘游戏，极端值敏感
闵可夫斯基距离	p次方和开p次根号	中	取决于p	否	需要灵活调整
马氏距离	考虑协方差矩阵	高	否	是	高维，特征相关
标准化欧氏距离	先标准化再欧氏距离	中	否	否	尺度差异大
汉明距离	对应位置不同数	低	否	否	二进制/离散数据