作为深度学习界的“裁判”，损失函数决定了模型是青铜还是王者。今天我们就来聊聊那些让模型又爱又恨的损失函数们！大家准备好，一起出发吧~~
一、损失函数：深度学习的“成绩单” 📝
想象一下你在玩投篮游戏🎯，每次投球后，篮筐都会告诉你离中心点有多远——这就是损失函数在深度学习中的作用！它量化了模型预测值与真实值之间的差距，就像个严格的教练，告诉模型：“小子，这次又偏了2厘米！”
为什么需要损失函数？
- 指导学习方向：通过反向传播告诉参数该往哪调整（梯度下降的灵魂伴侣⬇️）
- 评估模型性能：损失值越低，模型预测越准（学霸的满分答卷💯）
- 任务适配器：不同任务（分类/回归）需不同损失函数（就像篮球和足球用不同规则🏀⚽）
举个栗子🌰：预测房价时，预测值200万 vs 真实值210万，损失函数会冷酷地计算出这“10万”的代价！
二、常用损失函数🎯
1. Softmax 函数：神奇的“归一化大师”🧙♂️
原理：在分类任务里，我们常常会得到一组原始的分数（logits），这些分数有正有负，大小也不统一。Softmax 函数就像是一个神奇的“归一化大师”，它能把这些原始分数转换成一个概率分布。也就是说，它会把每个分数都变成一个 0 到 1 之间的数，而且所有分数转换后的概率加起来正好等于 1。这样，我们就可以很直观地看到模型对每个类别的预测概率啦！
公式：
对于一个输入向量 z=[z1,z2,...,zk]（k 是类别数），经过 Softmax 函数转换后，第 i 个类别的概率 
为：
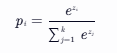
应用举例：假设我们有一个三分类任务，模型对一个样本的原始分数输出是 z=[2,1,0]。经过 Softmax 函数转换后：
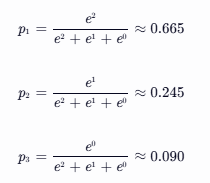
这样，我们就得到了模型对每个类别的预测概率啦！🎉
代码实现：
import numpy as np
def softmax(z):
exp_z = np.exp(z)
sum_exp_z = np.sum(exp_z)
return exp_z / sum_exp_z
z = np.array([2, 1, 0])
probabilities = softmax(z)
print("Softmax 后的概率分布:", probabilities)输出结果：
Softmax 后的概率分布: [0.66524096 0.24472847 0.09003057]2. 交叉熵损失函数：衡量预测与真实的“距离”📏
原理：交叉熵损失函数就像是衡量模型预测概率分布和真实概率分布之间“距离”的小尺子📏。在分类任务中，真实标签通常是一个 one-hot 编码的向量（只有一个元素是 1，其他都是 0）。交叉熵损失函数会计算模型预测的概率分布和这个 one-hot 编码的真实分布之间的差异。如果模型预测的概率和真实分布越接近，交叉熵损失函数的值就越小；反之，如果预测得相差很远，损失函数的值就会很大。
公式：
对于一个样本，真实标签为 y（one-hot 编码），模型预测的概率分布为 p，交叉熵损失函数 L 为：
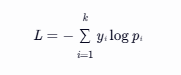
其中，k 是类别数。因为
是 one-hot 编码，所以只有真实类别的 
为 1，其他都为 0，所以公式可以简化为
。
应用举例：还是上面的三分类任务，假设真实类别是第一个类别（y=[1,0,0]），模型预测的概率分布是 p=[0.665,0.245,0.090]。那么交叉熵损失函数的值为：
代码实现：
import numpy as np
def cross_entropy_loss(y_true, y_pred):
return -np.sum(y_true * np.log(y_pred))
y_true = np.array([1, 0, 0])
y_pred = np.array([0.665, 0.245, 0.090])
loss = cross_entropy_loss(y_true, y_pred)
print("交叉熵损失:", loss)输出结果：
交叉熵损失: 0.40745515555555553. MAE 损失（平均绝对误差）：简单直接的“小裁判”👨⚖️
原理：MAE 损失就像是一个简单直接的“小裁判”👨⚖️。它计算的是模型预测值和真实值之间差的绝对值的平均值。不管预测值和真实值之间的差是正是负，MAE 损失都会把它们当成一样的“错误”来对待。
公式：
对于一个有 n 个样本的数据集，真实值为 
，模型预测值为 
，MAE 损失
为：
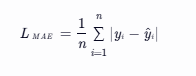
应用举例：假设我们有一个回归任务（虽然这里讲分类，但 MAE 也可以用于简单的分类概率回归情况，为了方便理解），有三个样本，真实值分别是 
，模型预测值是 
。那么 MAE 损失为：
代码实现：
import numpy as np
def mae_loss(y_true, y_pred):
return np.mean(np.abs(y_true - y_pred))
y_true = np.array([1, 2, 3])
y_pred = np.array([0.8, 2.2, 2.8])
loss = mae_loss(y_true, y_pred)
print("MAE 损失:", loss)输出结果：
MAE 损失: 0.2不过在分类任务中，我们一般不直接用 MAE 损失来优化模型，但了解它的原理有助于我们理解损失函数的概念哦！
4. MSE 损失（均方误差）：“放大错误”的“小放大镜”🔍
原理：MSE 损失就像是一个“放大错误”的“小放大镜”🔍。它计算的是模型预测值和真实值之间差的平方的平均值。和 MAE 损失不同的是，MSE 损失会对大的错误进行更大的惩罚，因为平方操作会让大的差值变得更大。
公式：
对于一个有 n 个样本的数据集，真实值为 
，模型预测值为 
，MSE 损失
为：
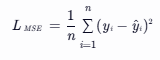
应用举例：还是上面的回归任务例子，MSE 损失为：
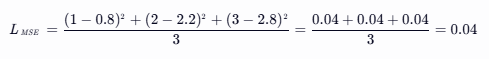
代码实现：
import numpy as np
def mse_loss(y_true, y_pred):
return np.mean((y_true - y_pred)**2)
y_true = np.array([1, 2, 3])
y_pred = np.array([0.8, 2.2, 2.8])
loss = mse_loss(y_true, y_pred)
print("MSE 损失:", loss)输出结果：
MSE 损失: 0.04同样，在分类任务中，MSE 损失也不是最常用的，但它的原理可以帮助我们更好地理解损失函数的设计思路。
5. Smooth L1 损失：融合 MAE 和 MSE 的“小精灵”🧚
原理：Smooth L1 损失就像是一个融合了 MAE 和 MSE 优点的“小精灵”🧚。它在预测值和真实值之间的差比较小的时候，表现得像 MSE 损失，会对小的错误进行一定的惩罚，但不会像 MSE 那样对大的错误过度放大惩罚；当差比较大的时候，它就表现得像 MAE 损失，对大的错误进行线性惩罚，这样就不会让模型对一些异常值过于敏感。
公式：
对于一个样本，真实值为 
，模型预测值为 
，Smooth L1 损失
为：
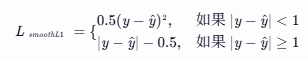
应用举例：假设真实值 
，模型预测值 
，因为 ∣2−1.5∣=0.5<1，所以使用 MSE 部分计算损失：
如果真实值 
，模型预测值 
，因为 ∣2−3∣=1≥1，所以使用 MAE 部分计算损失：
代码实现：
import numpy as np
def smooth_l1_loss(y_true, y_pred):
diff = np.abs(y_true - y_pred)
loss = np.where(diff < 1, 0.5 * diff**2, diff - 0.5)
return np.mean(loss)
y_true = np.array([2])
y_pred1 = np.array([1.5])
y_pred2 = np.array([3])
loss1 = smooth_l1_loss(y_true, y_pred1)
loss2 = smooth_l1_loss(y_true, y_pred2)
print("当预测值为 1.5 时的 Smooth L1 损失:", loss1)
print("当预测值为 3 时的 Smooth L1 损失:", loss2)输出结果：
当预测值为 1.5 时的 Smooth L1 损失: 0.125
当预测值为 3 时的 Smooth L1 损失: 0.5在分类任务中，Smooth L1 损失也不是最常用的，但在一些目标检测等任务中，它可是大显身手哦！
📊总结
| 损失函数 | 原理 | 适用场景 |
|---|---|---|
| Softmax | 将原始分数转换为概率分布 | 分类任务中模型输出层，将 logits 转换为概率 |
| 交叉熵损失 | 衡量模型预测概率分布和真实概率分布之间的差异 | 分类任务，尤其是多分类任务 |
| MAE 损失 | 计算预测值和真实值之间差的绝对值的平均值 | 回归任务，也可用于简单分类概率回归理解 |
| MSE 损失 | 计算预测值和真实值之间差的平方的平均值 | 回归任务，也可用于理解损失函数设计 |
| Smooth L1 损失 | 融合 MAE 和 MSE 的优点，对小错误和较大错误有不同惩罚方式 | 目标检测等任务 |
好啦，小伙伴们！今天我们一起探索了深度学习分类任务中常用的损失函数，就像进行了一场奇妙的魔法之旅🧙♀️。希望这些知识能帮助大家在深度学习的道路上越走越远，下次再见啦！👋
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
