理解正态矩阵与矩阵范数原理-优快云博客

1. Normal Equation

Given a matrix equation

$Ax = b$

the normal equation is that which minimizes the sum of the square differences between the left and right sides:

$A^T Ax = A^T b$
It is called a normal equation because $b - Ax$ is normal to the range of $A$ . Here, $A^T A$ is a normal matrix.

2. Normal Matrix

A square matrix $A$ is a normal matrix if

$[A, A^H] = A A^H - A A^H = 0$

where $[a, b]$ is the commutator and $A^H$ denotes the conjugate transpose.

正态矩阵，即具有性质 $A A^T = I$ 的矩阵，即矩阵 $A$ 的不同列正交。

3. 实对称矩阵的性质

实对称矩阵的特征值都是实数
实对称矩阵的特征向量都是实向量
实对称矩阵的属于不同特征值的特征向量正交（矩阵的属于不同特征值的特征向量线性无关，正交向量组必线性无关）
实对称矩阵的属于不同特征值的特征向量线性无关
$n$ 阶实对称矩阵恰有 $n$ 个线性无关的特征向量，进而有 $n$ 个单位正交的特征向量
实对称矩阵必可对角化
若两实对称矩阵有相同的特征值，则二者相似

4. 矩阵的迹

是所有对角元的和
是所有特征值的和

5. Hermitian matrix

该矩阵为一方阵， $a_{ij} = \overline{a_{ji}}$

6. Rayleigh quotient

In mathematics, for a given complex Heimitian matrix $M$ and nonzero vector $x$ , the Rayleigh quotient $R(M, x)$ , is defined as:

$R(M,x) := {x^{*} M x \over x^{*} x}.$

the conjugate transpose $x^{*}$

7. 向量范数

$x = (x_1, x_2, \cdots, x_n)$

1-范数：

$||x||_1 = \sum_{i=1}^n |x_i|$

2-范数：

$||x||_2 = \sqrt{|x_1|^2+|x_2|^2 + \cdots + |x_n|^2}$

$\infty$ -范数：

$||x||_{\infty} = \max_i |x_i|$

p-范数：

$||x||_p = \left( \sum_{i=1}^n |x_i|^p \right )^{1/p}$

8. 矩阵范数

$A = (a_{ij})_{m \times n} \in C^{m \times n}$

Frobenius范数，或简称F-范数：

$||A||_F = \left( \sum_{i=1}^m \sum_{j=1}^n |a_{ij}|^2 \right)^{1/2} = \left( \textrm{tr} (A^H A) \right )^{1/2}$

$\|A\|_F=\sqrt{\sum_{i=1}^m\sum_{j=1}^n |a_{ij}|^2}=\sqrt{\operatorname{trace}(A^{{}^*} A)}=\sqrt{\sum_{i=1}^{\min\{m,\,n\}} \sigma_{i}^2}$

列和范数、谱范数和行和范数：

$||A||_1 = \max_j \sum_{i=1}^m |a_{ij}|$

$||A||_2 = \sqrt{\lambda_1} \qquad \lambda_1 \ \textrm{is the largest eigen value of } \ A^H A$

$||A||_{\infty} = \max_i \sum_{j=1}^n |a_{ij}|$

If the singular values are denoted by σ_i, then the Schatten p-norm is defined by

$\|A\|_p = \left( \sum_{i=1}^{\min\{m,\,n\}} \sigma_i^p \right)^{1/p}. \,$

The most familiar cases are p = 1, 2, ∞. The case p = 2 yields the Frobenius norm, introduced before. The case p = ∞ yields the spectral norm, which is the matrix norm induced by the vector 2-norm (see above). Finally, p = 1 yields the nuclear norm (also known as the trace norm（迹范数）, or the Ky Fan 'n'-norm), defined as

$\|A\|_{*} = \operatorname{trace} \left(\sqrt{A^*A}\right) = \sum_{i=1}^{\min\{m,\,n\}} \sigma_i.$

$\|A\|_{\text{tr}}=\operatorname{trace}(\sqrt{A^*A})=\sum_{i=1}^{\min\{m,\,n\}} \sigma_{i}.$

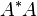(Here $\sqrt{A^*A}$ denotes a positive semidefinite matrix $B$ such that $BB=A^*A$ . More precisely, since $A^*A$ is a positive semidefinite matrix, its square root is well-defined.)