逻辑回归（Logistic regression）

实习完回学校，搞完了开题答辩，最近因为找工作需要，开始复习一些算法方面在笔试面试中会遇到的问题。用博客记录，之后要再看的话比较方便。如有错误，欢迎指正。

逻辑回归（Logistic regression）

一、逻辑回归是分类方法。
二、用的是sigmoid激活函数，特点：
1.将输入值映射到（0,1）区间。
2.函数图像连续且光滑，严格的单调递增函数，处处可导。
3.在0附近比较敏感。

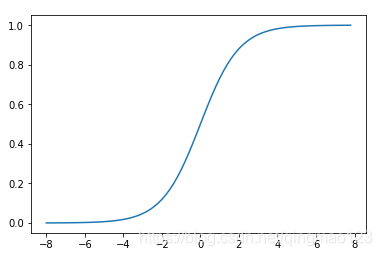
优点：形式简单，易使用和解释，速度快。
缺点：准确率不高（在离0越远的地方越不敏感，导致对那里的数据没有区分度）。收敛慢。

三、正则化
weightdecay的作用是将模型的复杂度降低。

正则化：防止过拟合。保留所有特征，减小不重要系数所占的比重。
问的比较多的是L1和L2的区别：
1.L1是模型各个参数的绝对值之和；L2是模型各个参数平方和的开方。
2.L1会趋向于产生少量的特征，而其他的特征都是0（稀疏矩阵）；L2会选择更多的特征，这些特征都会接近于0。

四、最小二乘法（Ordinary Least Square,OLS）
（1）对于函数$h_{\theta }(x1,...,xn)={\theta }_0+{\theta }_1\ast x_1+...+{\theta }_n\ast x_n$
（2）损失函数J(θ0,...,θn)=∑j=1m(∑i=0nθixi(j)−y(j))2J(θ_0,...,θ_n)=∑_{j=1}^{m}(∑_{i=0}^{n}θ_ix_i^{(j)}-y^{(j)})^2J(θ