【数据结构X.1】代码实现 二叉树的前序遍历，中序遍历，后序遍历和层次遍历

难点：

二叉树的主要难点在于理解其递归性质。
从根开始，左右孩子分别又是其左右孩子的根，子子孙孙无穷尽也，
如果能理解二叉树内部的相似性，那么剩下的实现就不难了。

后序遍历的非递归算法：

借助栈和一个记录上次访问的根节点的指针，可以实现后序遍历的非递归算法。
后序遍历的顺序为：左子，右子，根；
所以，后序遍历算法首先访问的必然是某棵子树的尽量靠左下的节点（虽然不一定是左子节点！例如图1）；

访问完该节点后，利用栈，读取该节点的父节点2（之前已经存在了栈里），然后向右走，如果右边已经访问过了，才最后读取这个父节点2。
按照左子，右子，根的顺序，会经过根节点2次，第一次是从根到左子节点，第二次是从根到右子节点，而只有从根的右子节点的全部节点已经访问过了，才能访问该根节点。

代码：

BiTree.h

#include <stack>
#include <iostream>
#include <malloc.h>
#include <queue>
typedef struct BiNode
{
    int data;
    struct BiNode *lchild, *rchild;
} BiNode, *BiTree;

/**
 * 前序遍历，递归
 */
void VisitTreeHead(BiTree tr)
{
    if (tr)
    {
        std::cout << char(tr->data) << " ";
        VisitTreeHead(tr->lchild);
        VisitTreeHead(tr->rchild);
    }
}

/**
 * 前序遍历，非递归
 */
void TreeNodeHead(BiTree tr)
{
    std::stack<BiNode *> s;
    BiNode *p = tr;
    while (!s.empty() || p)
    {
        if (p)
        {
            std::cout << char(p->data) << " ";
            s.push(p);
            p = p->lchild;
        }
        else
        {
            p = s.top();
            s.pop();
            p = p->rchild;
        }
    }
}

/**
 * 后序递归遍历二叉树
 */
void VisitTreeAfter(BiTree tr)
{
    if (tr)
    {
        VisitTreeAfter(tr->lchild);
        VisitTreeAfter(tr->rchild);
        std::cout << tr->data << " ";
    }
}

/**
 * 后序非递归遍历二叉树
 */
void TreeNodeAfter(BiTree tr)
{
    std::stack<BiNode *> s;
    BiNode *p = tr, *r = NULL;
    while (!s.empty() || p)
    {
        if (p)
        {
            s.push(p);
            p = p->lchild;
        }
        else
        {
            p = s.top();
            if (p->rchild && p->rchild != r)
            { //p有右孩子，且没有被访问过
                p = p->rchild;
                s.push(p);
                p = p->lchild;
            }
            else
            {
                s.pop();
                std::cout << char(p->data) << " ";
                r = p;
                p = NULL;
            }
        }
    }
}

/**
 * 创建一颗树
 */
BiTree CreateBTree(BiTree bt, bool isRoot)
{
    char ch;
    if (isRoot)
        std::cout << "Root:";

    std::cin >> ch;
    if (ch != '#')
    {
        isRoot = false;
        bt = (BiNode *)malloc(sizeof(BiNode));
        bt->data = ch;
        bt->lchild = NULL;
        bt->rchild = NULL;
        std::cout << "请输入" << ch << "的左孩子" << std::endl;
        bt->lchild = CreateBTree(bt->lchild, isRoot);
        std::cout << "请输入" << ch << "的右孩子" << std::endl;
        bt->rchild = CreateBTree(bt->rchild, isRoot);
    }
    return bt;
}

/**
 * 中序遍历二叉树:非递归
 */
void TreeNodeIn(BiTree tr)
{
    std::stack<BiNode *> s;
    BiNode *p = tr;
    while (!s.empty() || p)
    {
        if (p)
        {
            s.push(p);
            p = p->lchild;
        }
        else
        {
            p = s.top();
            s.pop();
            std::cout << char(p->data) << " ";
            p = p->rchild;
        }
    }
}

/**
 * 中序遍历二叉树：递归
 */
void VisitTreeIn(BiTree tr)
{
    if (tr != NULL)
    {
        VisitTreeIn(tr->lchild);
        std::cout << char(tr->data) << " ";
        VisitTreeIn(tr->rchild);
    }
}

/**
 * 层次遍历二叉树，
 */
void VisitTreeLevel(BiTree tr)
{
    std::queue<BiNode *> q;
    BiNode *p = tr;
    q.push(p);
    while (!q.empty())
    {
        p = q.front();
        q.pop();
        if (p)
        {
            std::cout << char(p->data) << " ";
            q.push(p->lchild);
            q.push(p->rchild);
        }
    }
}

BiTree_use.cpp

输入：

0
1
2
3
#
4
#
#
5
#
#
#
6
7
#
#
8
#
#

输出：

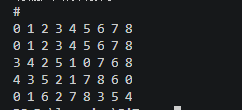
#include "BiTree.h"

int main()
{
    BiTree p;
    p = CreateBTree(p, true);
    VisitTreeHead(p);
    std::cout << std::endl;
    TreeNodeHead(p);
    std::cout << std::endl;
    TreeNodeIn(p);
    std::cout << std::endl;
    TreeNodeAfter(p);
    std::cout << std::endl;
    VisitTreeLevel(p);
    std::cout << std::endl;
}