【LeeCode】84. 柱状图中最大的矩形

最新推荐文章于 2025-03-14 02:00:00 发布

原创

最新推荐文章于 2025-03-14 02:00:00 发布 · 429 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #python #数据结构 #leetcode #栈

本文介绍了解决柱状图中寻找最大矩形面积问题的三种算法：暴力解法、分治算法及栈算法。详细解析了每种算法的实现思路、代码示例及其时间与空间复杂度。

LeeCode:做题网址
给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。
求在该柱状图中，能够勾勒出来的矩形的最大面积。
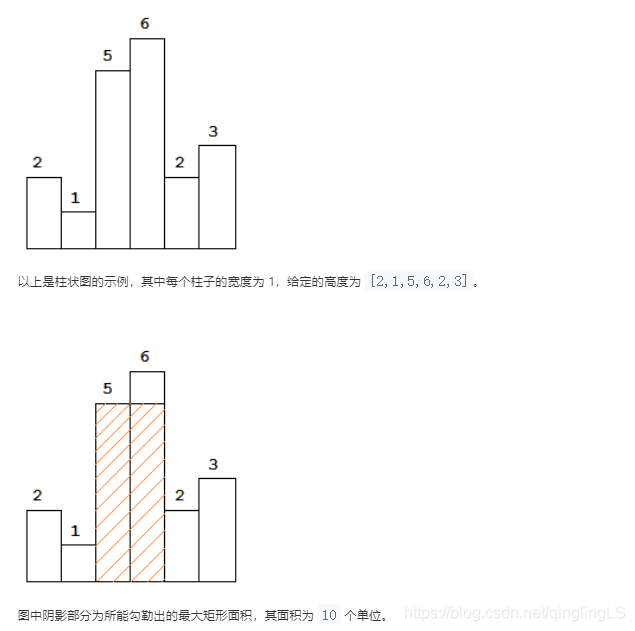
在这里插入图片描述
示例:

输入: [2,1,5,6,2,3]
输出: 10

1.暴力解法：

暴力遍历，每次都以第i个矩形为中心，左右拓展，如果没有高度小于第i个矩形，则保留大小，最后比较这些矩形。
思路： 两个柱子间矩形的高由它们之间最矮的柱子决定，所以目前遍历的第i个矩形的高度就决定了高，宽度由左右能拓展的宽度决定，所以左右的高度不能小于目前遍历的第i个矩形。

leeCode代码：

class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        rectangles=heights
        rec=[0]
        for i in range(0,len(rectangles)):
            left_i=i
            right_i=i
            while (left_i>0): # 如果左边可以拓展，左边坐标减一
                if(rectangles[left_i-1]>=rectangles[i]):
                  left_i-=1
                else:
                    break
            while(right_i<len(rectangles)-1): # 如果右边比当前高度高，右边坐标加1
                if(rectangles[right_i+1]>=rectangles[i]):
                    right_i+=1
                else:
                    break
            rec.append((right_i-left_i+

最低0.47元/天解锁文章