在学习吴恩达的深度学习系列课程,优化算法部分,权重更新部分讲到指数加权平均,查找到下面博文。此博文看配图,举例,也是吴恩达课程的总结,故此转载。
原作:cloud&ken
发表于:博客园
链接:https://www.cnblogs.com/cloud-ken/p/7723755.html
指数加权平均
举个例子,对于图中英国的温度数据计算移动平均值或者说是移动平均值(Moving average).
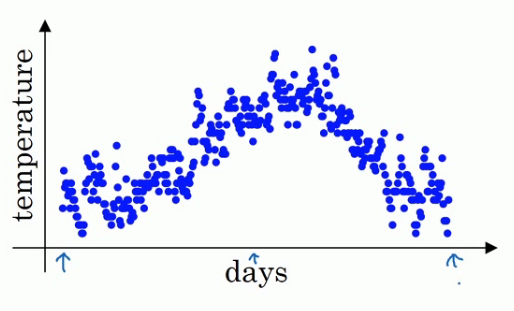

大体公式就是前一日的V值加上当日温度的0.1倍,如果用红线表示这个计算数值的话就可以得到每日温度的指数加权平均值.
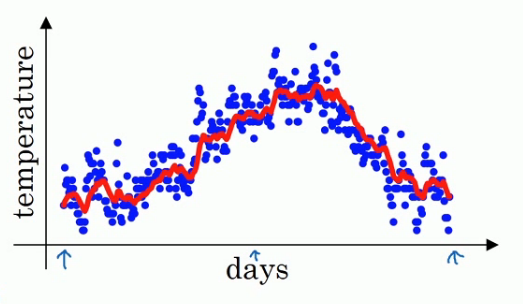
的理解,你可以将其认为该数值表示的是
天的平均值,例如如果这里取
是取0.9,那么这个V值表示的是十天以来的温度的加权平均值.如果我们设置
- 值是0.98那么我们就是在计算50天内的指数加权平均,这时我们用图中的绿线表示指数加权平均值
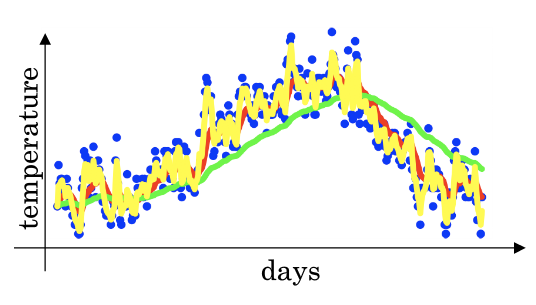
得到的曲线要平坦一些,是因为你多平均了几天的温度.所以波动更小,更加平坦.缺点是曲线向右移动,这时因为现在平均的温度值更多,所以会出现一定的延迟.对于
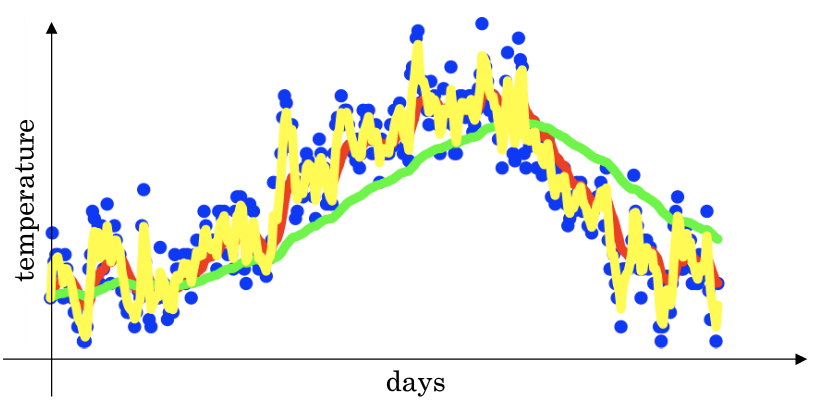
这个值的理解在于有0.98的权重给了原先的值,只有0.02的权重给了当日的值.我们现在将
- 作图运行后得到黄线,由于仅平均了两天的温度,平均的数据太少,所以得到的曲线有更多的噪声,更有可能出现异常值,但是这个曲线能更快的适应温度变化,所以指数加权平均数经常被使用.
- 在统计学中,它常被称为指数加权移动平均值
2.4 理解指数加权平均
公式:
为0.9时,得到的是
红线,
为0.98,得到的是
绿线,
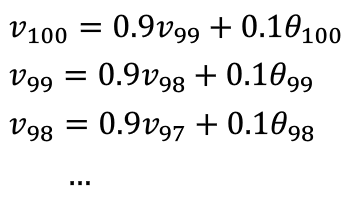
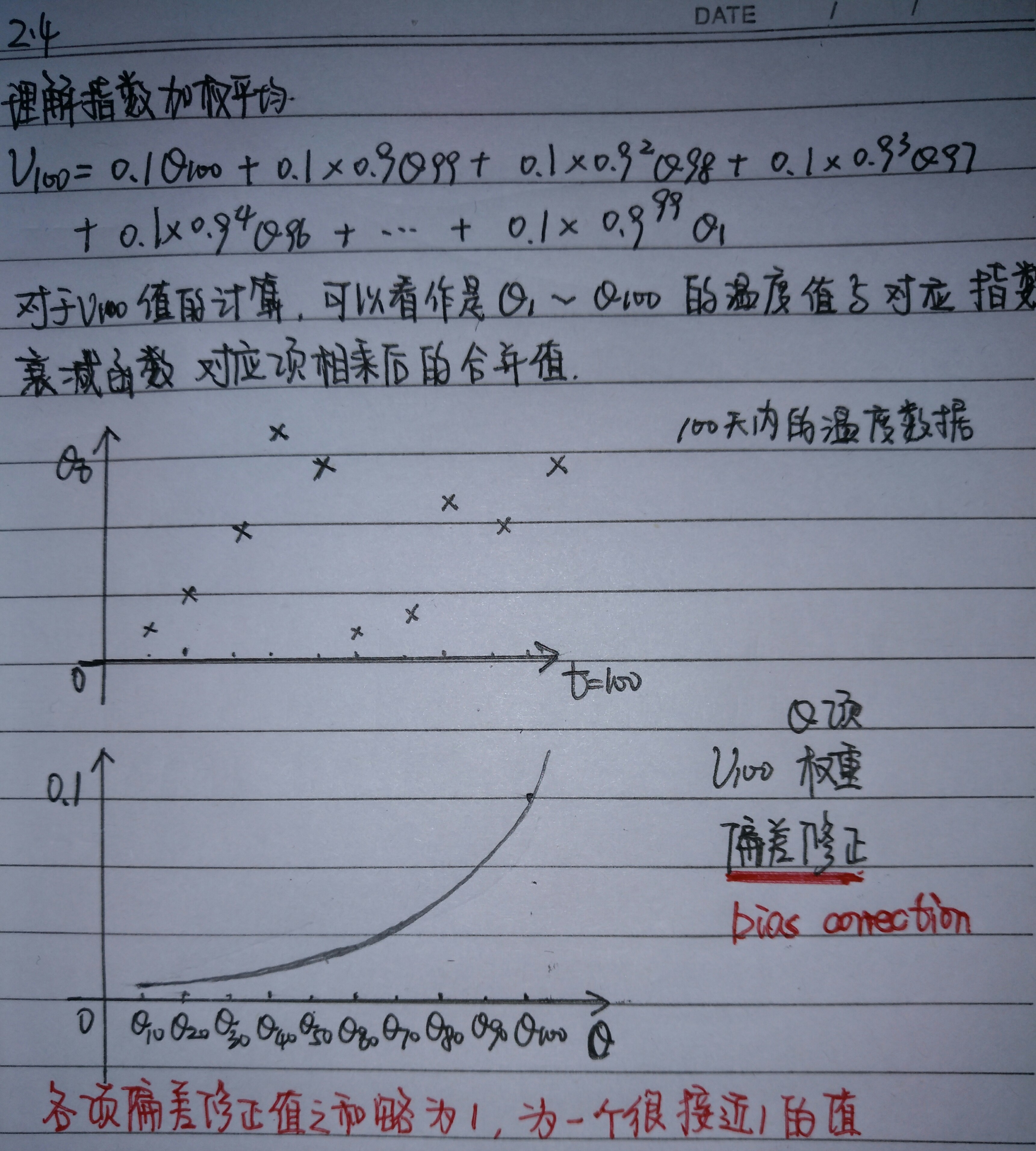
,也就是说对于$\beta=0.9而言
\frac{1}{3}$
对于
,即50天之后权重就会下降到
即有
优势
实际处理数据时,我们会使用以下公式:
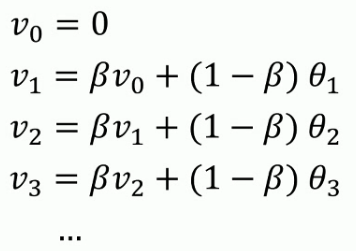
- 内存代码仅仅占用一行数字而已,不断覆盖掉原有的V值即可,只占单行数字的存储和内存.虽然不是最精确的计算平均值的方法,但是相比于原有的计算平均值需要保存所有数据求和后取平均的方法效率更高和资源占用率大大减小.所以在机器学习中大部分采用指数加权平均的方法计算平均值.
2.5 指数加权平均的偏差修正
当我们取
时,实际上我们得到的不是绿色曲线,而是紫色曲线,因为使用指数加权平均的方法在前期会有很大的偏差,为此我们引入了偏差修正的概念
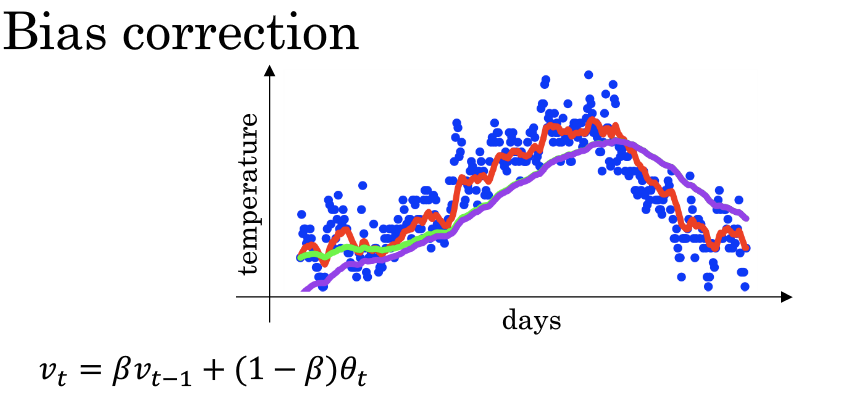
指数加权平均公式:
带修正偏差的指数加权平均公式:

补充
在机器学习中,在计算指数加权平均数的大部分时候,大家不太在乎偏差修正,大部分宁愿熬过初始阶段,拿到具有偏差的估测,然后继续计算下去.
如果你关心初始时期的偏差,修正偏差能帮助你在早期获得更好的估测

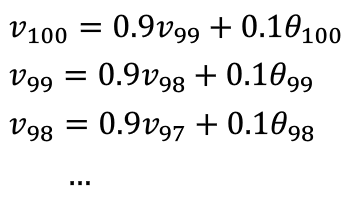

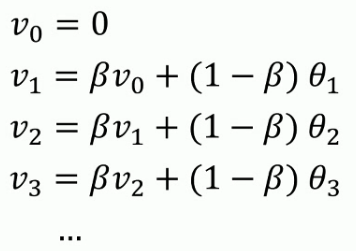










 本文深入探讨了机器学习中常用的优化算法——指数加权平均。文章通过英国气温数据实例,详细解析了不同β值下指数加权平均的效果,包括其在平滑数据、减少噪声方面的优势,以及如何通过偏差修正提高初期估算准确性。
本文深入探讨了机器学习中常用的优化算法——指数加权平均。文章通过英国气温数据实例,详细解析了不同β值下指数加权平均的效果,包括其在平滑数据、减少噪声方面的优势,以及如何通过偏差修正提高初期估算准确性。




















 617
617

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








