寻找和为定值的数-优快云博客

本文链接：https://blog.youkuaiyun.com/qiki_tangmingwei/article/details/78591169

寻找和为定值的k个数

问题描述

输入两个整数n和sum，要求从正整数数列中随意取出几个数，使得它们的和等于sum，将其中所有可能的组合列出来

解法：递归法

此题是在n个数中找和为sum的任意组合，那么可以将问题转化为：

1）若选第n个数，则在剩余的n-1个数中找和为sum-val(n)的数

2）若不选第n个数，则在剩余的n-1个数中找和为sum的数

这里的n是不定的，所以当代码层层递归后，最后问题变成了在数列中找一个目标值，使它的值与sum-val(i)-val(j)-val(k)..的值相等。

下面代码给出的是求和为定值的任意个数的组合

/**************************
Author:tmw
date:2017-11-21
update:2019-3-22
***************************/
#include <stdio.h>
#include <stdlib.h>

int result[100] = {0};//将结果数组定义成全局变量是避免在递归调用函数时，重复申请内存空间
int j = 0;
void choose_k_numbers_equal_to_sum(int* array , int array_len , int sum)
{
    //输入合法性检查 && 递归出口
    if( !array || array_len <=0 )//sum也可以为负数
        return;
    //结果打印
    if( j > 0 )
    {
        if( array[array_len-1] == sum )//如果一直递归，这个sum值和n值是不断变化的：sum-val(i)-val(j)-val(k)..
        {
            int i;
            for( i = 0 ; i < j ; i++ )
                printf("%d + ",result[i]);
            //此时array[n-1]并没有赋入result数组中，因此要单独打印
            printf("%d \n",array[array_len-1]);
        }
    }
    result[j++] = array[array_len-1];
    choose_k_numbers_equal_to_sum(array,array_len-1,sum-array[array_len-1]);//放n，前n-1个数满足sum-val(n)
    j--;//不放n时，游标要撤回
    choose_k_numbers_equal_to_sum(array,array_len-1,sum);//不放n，前n-1个数满足sum
}

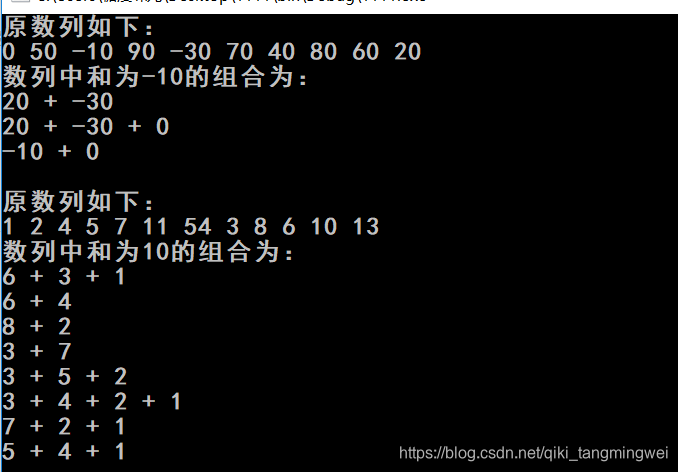
测试代码及结果：

int main()
{
    int i;
    int array2[10] ={0,50,-10,90,-30,70,40,80,60,20};
    printf("原数列如下：\n");
    for(i=0; i<10; i++)
        printf("%d ",array2[i]);
    printf("\n");
    printf("数列中和为-10的组合为：\n");
    choose_k_numbers_equal_to_sum(array2,10,-10);

    printf("\n");

    int a[12] = {1,2,4,5,7,11,54,3,8,6,10,13};
    printf("原数列如下：\n");
    for(i=0;i<12;i++)
        printf("%d ",a[i]);
    printf("\n");
    printf("数列中和为10的组合为：\n");
    choose_k_numbers_equal_to_sum(a,12,10);

    return 0;
}

下面代码给出的是求和为定值的任意k个数的组合组合

/***********************************************
下面代码给出的是求和为定值的任意k个数的组合
Author:tmw
date:2017-11-21
update:2019-3-22
************************************************/
#include <stdio.h>
#include <stdlib.h>

int result[100] = {0};//将结果数组定义成全局变量是避免在递归调用函数时，重复申请内存空间
int j = 0;
void choose_k_numbers_equal_to_sum(int* array , int array_len , int sum , int k )
{
    //输入合法性检查 && 递归出口
    if( !array || array_len <=0 )
        return;
    //结果打印
    if( j > 0 )
    {
        if( array[array_len-1] == sum && j == k - 1)//如果一直递归，这个sum值和n值是不断变化的：sum-val(i)-val(j)-val(k)..
        {
            int i;
            for( i = 0 ; i < j ; i++ )
                printf("%d + ",result[i]);
            //此时array[n-1]并没有赋入result数组中，因此要单独打印
            printf("%d \n",array[array_len-1]);
        }
    }
    result[j++] = array[array_len-1];
    choose_k_numbers_equal_to_sum(array,array_len-1,sum-array[array_len-1],k);//放n，前n-1个数满足sum-val(n)
    j--;//不放n时，游标要撤回
    choose_k_numbers_equal_to_sum(array,array_len-1,sum,k);//不放n，前n-1个数满足sum
}

测试代码及结果:

int main()
{
    int i;
    int array2[10] ={0,50,-10,90,-30,70,40,80,60,20};
    printf("原数列如下：\n");
    for(i=0; i<10; i++)
        printf("%d ",array2[i]);
    printf("\n");
    printf("数列中和为-10的3个数的组合为：\n");
    choose_k_numbers_equal_to_sum(array2,10,-10,3);

    printf("\n");

    int a[12] = {1,2,4,5,7,11,54,3,8,6,10,13};
    printf("原数列如下：\n");
    for(i=0;i<12;i++)
        printf("%d ",a[i]);
    printf("\n");
    printf("数列中和为10的3个数的组合为：\n");
    choose_k_numbers_equal_to_sum(a,12,10,3);

    return 0;
}