31-最大连续子数组和

最新推荐文章于 2025-06-23 20:04:27 发布

原创最新推荐文章于 2025-06-23 20:04:27 发布 · 882 阅读

4 ·

CC 4.0 BY-SA版权

文章标签：

#最大连续子数组和 #搜索 #遍历 #c语言

剑指offer 同时被 3 个专栏收录

45 篇文章

订阅专栏

经典算法

21 篇文章

订阅专栏

动态规划

19 篇文章

订阅专栏

问题描述

给定一个整数数组，数组里可能有正数、负数和0。数组中连续的一个或多个整数组成一个子数组，每个子数组都有一个和。求所有子数组的和的最大值。

方法1–暴力搜索

从数组位置0出发，依次顺序递加后，和值的最大值`
从数组位置1出发，依次顺序递加后，和值在前两轮最大值（因为满足最大条件后，最大值才更新；
…
直到遍历到数组最后一个位置numSize-1 ，和值在前numSize轮的最大值，即本题最终答案

暴力搜索代码

/*******************************
【方法一：暴力搜索】----复杂度O(n^2)
Author:tmw 
date:2017-11-21 
*******************************/
#include <stdio.h>
#include <stdlib.h>
#include <limits.h>

int maxSubArray(int* nums, int numsSize)
{
    int max = INT_MIN;
    int i,j,sum;

    for( i = 0 ; i < numsSize ; i++ )
    {
        sum = 0;
        for( j = i ; j < numsSize ; j++)
        {
            sum = nums[j] + sum;
            if( sum > max )
                max = sum;
        }
        printf("第%d轮最大值为:%d \n",i,max);
    }
    return max;
}

测试代码及结果

int main()
{
    printf("测试代码!\n");
    int i;

    int a1[8] = {1,-2,3,10,-4,7,2,-5};
    int result1 = maxSubArray(a1,8);
    printf("原数组为：");
    for(i = 0 ; i < 8 ; i++ )
        printf("%d ",a1[i]);
    printf("最大子数组和为 %d\n",result1);

    int a2[9] = {-2,1,-3,4,-1,2,1,-5,4};
    int result2 = maxSubArray(a2,9);
    printf("原数组为：");
    for(i = 0 ; i < 9 ; i++ )
        printf("%d ",a2[i]);
    printf("最大子数组和为 %d\n",result2);

    return 0;
}

测试结果

方法2–动态规划

这个问题可以看成：现在有一个合集，当前元素a[i]要不要加入这个和集，或者自己重新开启一个合集；
作出选择的关键在于，使得合集值最大

我们知道，正数相加一定会使和集增大，因此，判定因素变成了：

如果当前合集为正，则a[i]加入这个合集
如果当前合集为负，则a[i]重新开启一个合集

写成数学表达就是：sum = max(curren_sum,0)+a[i],式子中，curren_sum为当前和集的和，sum记录和集的最大和

动态规划理解参考：
http://www.cnblogs.com/boring09/p/4252780.html http://www.cnblogs.com/bourbon/archive/2011/08/23/2151044.html

最大连续子数组和代码

下面的代码直接求出最大连续子数组的和

/******************************
【方法二：动态规划】----复杂度O(n)
Author:tmw 
date:2017-11-21 
******************************/
#define max(a,b) (a>b?a:b)
int max_sub_array_sum( int *array , int array_len )
{
    int i;
    int sum = 0;
    int temp_sum;
    int curren_sum = array[0];//array[i]从1开始找起
    for( i = 1 ; i < array_len ; i++ )
    {
        temp_sum = curren_sum;//保存一下curren_sum变化前的值
        current_sum = max( current_sum+array[i],array[i] );
        //后面的sum为sum变化前的值，sum更新的前提是：新的sum要比原的sum大
        sum = max( sum, max(current_sum,temp) );
    }
    return sum;
}

测试结果

测试代码如下：

int main()
{
    printf("测试代码!\n");
    int i;

    int a1[8] = {1,-2,3,10,-4,7,2,-5};
    printf("原数组为：");
    for(i = 0 ; i < 8 ; i++ )
        printf("%d ",a1[i]);
    printf("\n");
    int result1 = max_sub_array_sum(a1,8);
    printf("最大子数组和为 %d\n",result1);

    printf("\n");

    int a2[9] = {-2,1,-3,4,-1,2,1,-5,4};
    printf("原数组为：");
    for(i = 0 ; i < 9 ; i++ )
        printf("%d ",a2[i]);
    printf("\n");
    int result2 = max_sub_array_sum(a2,9);

    printf("最大子数组和为 %d\n",result2);

    return 0;
}

测试结果如下：

功能改进-要求输出子数组的起始位置和结束位置

**【功能改进】**找到最大连续子数组和的下标并输出这个最大子数组和最大子数组和

/***************
update: 2019-4-8
author: tmw
***************/
#define max(a,b) (a>b?a:b)
int maxSubArray(int* array, int len)
{
    int i=0;

    int cur_sum = array[0];
    int max_sum = array[0];
    int start = 0;
    int end = len-1;

    int temp;
    int mark_start = 0; //起始游标标记
    for(i=1; i<len; i++)
    {
        temp = cur_sum;

        /**说明在f(i-1),f(i-1)+a[i],a[i]三者中，
           - f(i-1)是相对于a[i]的极小项，即f(i-1)<f(i-1)+a[i]<a[i]
           - 所以最大子数组和的首位从a[i]开始，即mark_start=i
        **/
        if(cur_sum+array[i]<array[i])
        {
            mark_start = i;
            cur_sum = array[i];  //{-1,11,-8,1,2,-7,4,-3,-1,-1};
        }
        else
            cur_sum = array[i]+cur_sum;

        // max_sum = max(max_sum,max(temp,cur_sum));
        if (max_sum < max(temp,cur_sum)) {
            start = mark_start; //最大值有更新才敲定start游标，否则start游标不轻易变动
            max_sum = max(temp,cur_sum);
        }
    }

    //已知子数组和&&起始位置，求结束位置
    i = start;
    int sub_sum = 0;
    for(i=start; i<len; i++)
    {
        sub_sum += array[i];
        if(sub_sum == max_sum)
        {
            end = i;
            break;
        }
    }
    printf("start = %d, end = %d, maxSubArray=%d\n",start,end,max_sum);
    return max_sum;
}

测试结果

测试代码如下：

int main()
{
    int a1[9] = {-2,1,-3,4,-1,2,1,-5,4};
    int a2[12] = {1,-2,3,10,-4,7,2,-5,10,-1,2,-3};
    int a3[10] = {-1,11,-8,1,2,-7,4,-3,-1,-1};
    int a4[10] = {1,11,8,1,2,7,4,3,1,1};
    int a5[10] = {-1,-11,-8,-1,-2,-7,-4,-3,-1,-1};
    int i;
    printf("原始数组:\n");
    for(i=0; i<9; i++)
        printf("%d ",a1[i]);
    printf("\n");
    printf("%d\n",maxSubArray(a1,9));

    printf("\n");

    printf("原始数组:\n");
    for(i=0; i<12; i++)
        printf("%d ",a2[i]);
    printf("\n");
    maxSubArray(a2,12);

    printf("\n");

    printf("原始数组:\n");
    for(i=0; i<10; i++)
        printf("%d ",a3[i]);
    printf("\n");
    printf("%d\n",maxSubArray(a3,10));

    printf("原始数组:\n");
    for(i=0; i<10; i++)
        printf("%d ",a4[i]);
    printf("\n");
    printf("%d\n",maxSubArray(a4,10));

    printf("原始数组:\n");
    for(i=0; i<10; i++)
        printf("%d ",a5[i]);
    printf("\n");
    printf("%d\n",maxSubArray(a5,10));

    return 0;
}

执行结果：

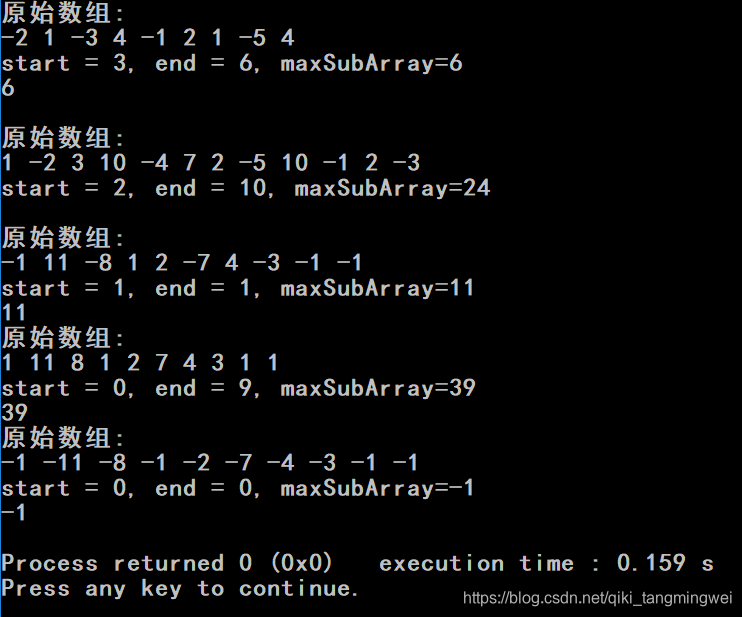
方法3–分治法

首先将其分成两半A[l…m]和A[m+1…r]，其中m=(l+r)/2，并分别求递归求出这两半的最大子串和，不妨称为left，right
A[l…r]的连续子串和可能出现在左半边（即left），或者可能出现在右半边（即right），还可能出现在横跨左右两半的地方
按照方法一，从中间向两边扫，求最大值。

那么这个分治法的主要作用在于缩小了方法一的扫描范围

分治法代码

int max( int a , int b )
{
    a = (b > a ? b : a);
    return a;
}
//构造分治法子函数
int dividConquer( int *nums , int l , int r )
{
    int middle,left,right;//存储左、中、右值的变量
    int m;//中间值的下标
    int i,j,temp,result;

    if( l == r )
        return nums[l];//确定分治边界

    m = ( l + r ) / 2;
    middle = nums[m];
    left = dividConquer( nums , l , m );
    right = dividConquer( nums , m+1 , r );

    //这个middle的值可以看成一个不断包容吞并和值最大的值，
    //当递归进行到r = l+1时，middle记录的值是只有两个值存在下的最大和值（要么是原位置m上的值，要么是两个值的和值，反正取只有两个数存在下的最大值）
    //所以可以判断，当这两个值庞大到左右两个部分的时候，middle记录的是要么包含原位置m上的值与左半支或者右半支的和值，要么不包含原位置m下的值，就是左半支或右半支返回的最大值
    //但是注意，middle并不代表本题的最大值，因为它跳到最外层循环的时候，返回的值是
    //1）本身m位置下的值
    //2）m位置下的值与左半支或右半支的和值
    //3）m位置下的值与左右半支总和值
    //三种情况下的最大值，总之middle的值是包含m位置下的值的最大和值情况，但答案可能是不包含m位置下的值，可能在左分支最大值也可能在右分支最大值，因此
    //result = max( max(left , right ) , middle );正是做了最大值要么包括m位置下的值，要么不包括m位置下的值（取左边或右边）这一件事。
    for( i = m-1 , temp = middle ; i >= l ; i-- )
    {
        temp = nums[i] + temp;
        middle = max( temp , middle );
    }

    for( j = m+1 , temp = middle ; j <= r ; j++ )
    {
        temp = nums[j] + temp;
        middle = max( temp , middle );
    }

    result = max( max(left , right ) , middle );
    return result;
}

int maxSubArray(int* nums, int numsSize)
{
    return dividConquer( nums , 0 , numsSize - 1 );;
}