numpy实现的soft-max方法

最新推荐文章于 2025-05-29 10:34:16 发布

原创最新推荐文章于 2025-05-29 10:34:16 发布 · 7.3k 阅读

5 ·

CC 4.0 BY-SA版权

文章标签：

#机器学习 #神经网络 #线性代数 #python #numpy

机器学习专栏收录该内容

1 篇文章

订阅专栏

本文介绍了在机器学习中广泛使用的softmax方法，特别是在神经网络中。通过numpy的向量运算可以简便实现softmax，但原始实现可能面临数值溢出问题。为解决此问题，文章提出利用softmax函数的性质，通过调整分子和分母，尤其是通过设置logC = -max(f)进行数值偏移，确保最大值为零，从而避免指数溢出。最终给出的优化实现确保了计算的稳定性。

numpy实现的soft-max方法

soft-max

soft-max

soft-max 是人工智能领域被大范围使用的一个方法。
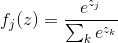
在这里插入图片描述

借助numpy的向量运算，可以很容易地实现:

import numpy as np

def softmax( f ):
    # 坏的实现: 数值问题
    return np.exp(f) / np.sum(np.exp(f))

但是，上面的实现存在问题。 e^f 存在很容易因为数值过大导致溢出的问题。

>>> softmax( np.array([123, 456, 789])  )
__main__:3: RuntimeWarning: overflow encountered in exp
__main__:3: RuntimeWarning: invalid value encountered in divide

要解决这个问题，我们需要使用 soft-max 一个很重要的特性：
如果我们将soft-max函数的分子和分母，都乘以常数C, 我们将得到以下等式：
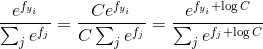
在这里插入图片描述
我们可以任意的选取C 的值, 这不会改变任何结果。也就是说，soft-max函数参数的数组中的元素数值本身并不重要的，重要的是他们之间的数值差异。我们同时增加/减少任意数值而不会改变结果。

>>> softmax( np.array([12,25,44]) )
array([  1.26641655e-14,   5.60279641e-09,   9.99999994e-01])
>>> # add 100 to all entries , it keeps the same result
>>> softmax(  np.array([12+100,25+100,44+100]) )
array([  1.26641655e-14,   5.60279641e-09,   9.99999994e-01])

一个常用选择是设置 logC = -max(f), 效果就是我们将数组内的所有元素都同时进行偏移(增加或减小)，以使得最大值为零。

经过这样的处理，指数 e^f 就不再会有溢出的问题了。最后的实现如下:

def softmax( f ):
    # instead: first shift the values of f so that the highest number is 0:
    f -= np.max(f) # f becomes [-666, -333, 0]
    return np.exp(f) / np.sum(np.exp(f))  # safe to do, gives the correct answer

>>> softmax( np.array([123, 456, 789])  )
array([5.75274406e-290, 2.39848787e-145, 1.00000000e+000])