[NOIP2011提高组Day1T2]选择客栈

题目链接

[NOIP2011提高组Day1T2]选择客栈

题目描述

丽江河边有 $n$ 家很有特色的客栈，客栈按照其位置顺序从 $1$ 到 $n$ 编号。每家客栈都按照某一种色调进行装饰（总共 $k$ 种，用整数 $0\sim k-1$ 表示），且每家客栈都设有一家咖啡店，每家咖啡店均有各自的最低消费。

两位游客一起去丽江旅游，他们喜欢相同的色调，又想尝试两个不同的客栈，因此决定分别住在色调相同的两家客栈中。晚上，他们打算选择一家咖啡店喝咖啡，要求咖啡店位于两人住的两家客栈之间（包括他们住的客栈），且咖啡店的最低消费不超过 $p$ 。

他们想知道总共有多少种选择住宿的方案，保证晚上可以找到一家最低消费不超过 $p$ 元的咖啡店小聚。

输入格式

共 $n+1$ 行。

第一行三个整数 $n,k,p$，每两个整数之间用一个空格隔开，分别表示客栈的个数，色调的数目和能接受的最低消费的最高值；

接下来的 $n$ 行，第 $i+1$ 行两个整数，之间用一个空格隔开，分别表示 $i $ 号客栈的装饰色调 $a_i$ 和 $i$ 号客栈的咖啡店的最低消费 $b_i$。

输出格式

一个整数，表示可选的住宿方案的总数。

输入输出样例 #1

输入 #1

5 2 3 
0 5 
1 3 
0 2 
1 4 
1 5

输出 #1

3

说明/提示

样例解释

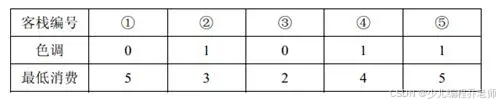
2 人要住同样色调的客栈，所有可选的住宿方案包括：住客栈①③，②④，②⑤，④⑤，但是若选择住 $4,5$号客栈的话，$4,5$ 号客栈之间的咖啡店的最低消费是 $4$ ，而两人能承受的最低消费是 $3$ 元，所以不满足要求。因此只有前 $3$ 种方案可选。

数据范围

• 对于 $30\%$ 的数据，有 $n\le 100$ ；
• 对于 $50\%$ 的数据，有 $n\le 1000$；
• 对于 $100\%$ 的数据，有 $2\le n\le 2\times 10^5$，$1\le k\le 50$，$0\le p\le 100$，$0\le b_i\le 100$。

样例分析

有$5$家客栈，$2$种色调，在最低消费不超过$3$的情况下，如下图所示：

• 对于③号客栈，由于其价格$2\le 3$，那么③号客栈左边同色调的客栈都满足要求，有$1$种方案可选，即①③。
• 对于④号客栈，由于其价格$4>3$，要满足到④号客栈之间存在最低消费不超过$3$的客栈，那么③号客栈（最低消费为$2$）以及左边同色调的客栈都满足要求，有$1$种方案可选，即②④。
• 对于⑤号客栈，由于其价格$5>3$，要满足到⑤号客栈之间存在最低消费不超过$3$的客栈，那么③号客栈（最低消费为$2$）以及左边同色调的客栈都满足要求，有$1$种方案可选，即②⑤。

因此，一共有$3$种满足条件的方案。

算法思想

通过上述分析，可以得到一种朴素的算法思想，枚举每个客栈，对于第i个客栈来说：

• 如果其价格b[i] <= p，统计$1\sim i-1$有多少个与其色调a[i]相同的客栈
• 否则其价格b[i] > p，找到i左边最接近i的客栈j，并且其价格b[j]<=p，统计$1\sim j$有多少个与其色调a[i]相同的客栈

时间复杂度

在枚举每个客栈的同时，要枚举与之匹配的客栈，因此时间复杂度为$O(n^2)$，尚需优化。

代码实现

#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 5;
int a[N], b[N]; //色调和价格
int main()
{
    int n, k, p;
    scanf("%d%d%d", &n, &k, &p);
    for(int i = 1; i <= n; i ++) scanf("%d%d", &a[i], &b[i]);    
    long long ans = 0;
    for(int i = 1; i <= n; i ++)
    {
        int cnt = 0;
        if(b[i] <= p) //如果当前客栈的价格不超过p，那么统计其左边有多少个同色调的客栈
        {
            for(int j = 1; j < i; j ++)
                if(a[j] == a[i]) cnt ++;
        }
        else //如果当前客栈价格大于p
        {
            int m = i - 1;
            while(b[m] > p) m --; //找到i左边最靠近i并且小于价格p的客栈
            //统计1~m有多少个同色调的客栈
            for(int j = 1; j <= m; j ++)
                if(a[j] == a[i]) cnt ++;
        }
        ans += cnt;
    }
    cout << ans << endl;
    return 0;
}

算法优化

在上述算法中，需要统计两种情况下与i色调相同的客栈数量：

• 当b[i] <= p时，统计$1\sim i-1$与i色调相同的客栈数量
• 当b[i] > p 时，需要找到i左边最接近i的客栈j，且其价格b[j]<=p，统计$1\sim j$与i色调相同的客栈数量

这里不妨设j表示最接近i的客栈编号，其价格b[j]<=p；并设sum[a[i]]表示$1\sim j$与i色调相同的客栈数量

• 当b[i] <= p时，将j移动到i，同时将色调为a[j]的客栈数量增加$1$，即sum[a[j]] ++。那么，$1\sim i-1$与i色调相同的客栈数量为sum[a[i]] - 1（去掉i号客栈）
• 当b[i] > p 时，$1\sim j$与i色调相同的客栈数量为sum[a[i]]

这样，只需要枚举枚举每个客栈就可以了。

时间复杂度

枚举每个客栈的时间复杂度为$O(n)$。

代码实现

#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 5;
int a[N], b[N]; //色调和价格
long long sum[N]; //sum[c]表示当前色调为c的客栈个数
int main()
{
    int n, k, p;
    scanf("%d%d%d", &n, &k, &p);
    for(int i = 1; i <= n; i ++) scanf("%d%d", &a[i], &b[i]);
    
    long long ans = 0;
    for(int i = 1, j = 0; i <= n; i ++) //j表示i左边第一个价格小于等于p的客栈编号
    {
        if(b[i] <= p) //当前客栈价格小于等于p，那么另一个客栈就可以在i的左边选颜色相同即可
        {
            while(j + 1 <= i) //将j移动到价格小于等于p的客栈位置
            {
                j ++;
                sum[a[j]] ++;
            }
            ans += sum[a[i]] - 1; //减去i客栈自己，两个人住不同客栈
        }
        else ans += sum[a[i]]; //第一个客栈在1~j中选，颜色为a[i]的方案数
    }
    cout << ans << endl;
    return 0;
}