C++题解之对顶堆：中位数

中位数

题目链接：洛谷P1168 中位数

题目描述

给定一个长度为 $N$ 的非负整数序列 $A$，对于前奇数项求中位数。

输入格式

第一行一个正整数 $N$。

第二行 $N$ 个正整数 $A_{1\dots N}$。

输出格式

共 $\lfloor \frac{N+1}{2}\rfloor$ 行，第 $i$ 行为 $A_{1\dots 2i-1}$ 的中位数。

样例 #1

样例输入 #1

7
1 3 5 7 9 11 6

样例输出 #1

1
3
5
6

提示

对于 $20\%$ 的数据，$N\le 100$；

对于 $40\%$ 的数据，$N\le 3000$；

对于 $100\%$ 的数据，$1\le N\le 100000$，$0\le A_i\le 10^9$。

算法思想：对顶堆

对顶堆，就是由一个大根堆和一个小根堆，两个堆组成的数据结构，如下图所示：

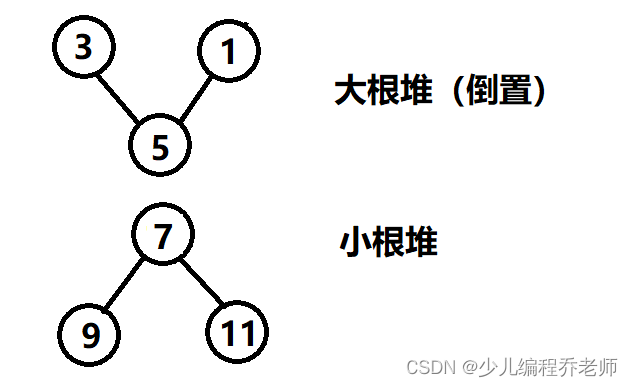
如果把大根堆看成一个上宽下窄的三角形，把小根堆看成一个上窄下宽的三角形，那么对顶堆就可以被看成一个“陀螺”或者一个“沙漏”，通过这两个堆的上下组合，我们可以把一组数据分别加入到对顶堆中的大根堆和小根堆，以维护不同的需要。

例如，加入数字$6$后，求这$7$个数的中位数。可以将$6$插入到大根堆中（如下图所示）。

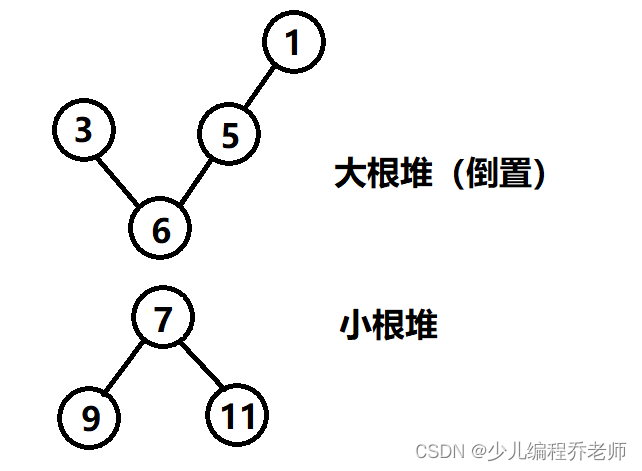
$7$个数的中位数就是求第$4$小的数，只需要在大根堆中保留$3$个数，即将大根堆堆顶插入到小根堆中，那么小根堆的堆顶元素就是第$4$小的数，也就是$6$，如下图所示。

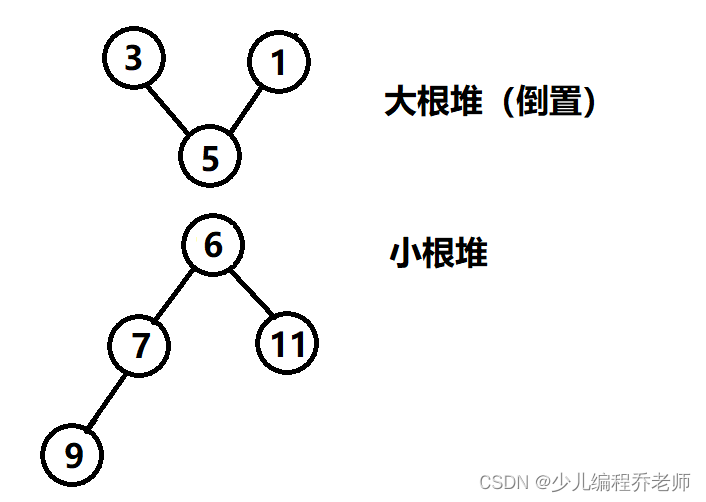
具体步骤

• 遍历整数序列 $A$的每个数，对于第$i$个数$a[i]$：
  • 将$a[i]$插入到大根堆中
  • 如果是奇数项，则求第$k$小的数
    • 将大根堆的堆顶插入到小根堆，只保留$k-1$项。
    • 输出小根堆的堆顶
    • 为了保证大根堆中至少有$k$项，再将小根堆的堆顶放回大根堆

代码实现

时间复杂度：$nlog(n)$

#include <iostream>
#include <queue>
using namespace std;
const int N = 1e5 + 10;
int a[N];
int main()
{
    priority_queue<int> q1; //大根堆
    priority_queue<int, vector<int>, greater<int>> q2; //小根堆
    
    int n;
    scanf("%d", &n);
    for(int i = 1; i <= n; i ++) scanf("%d", a + i);
    
    for(int i = 1; i <= n; i ++) 
    {
        q1.push(a[i]);
        if(i % 2) {
            int k = i / 2 + 1;
            while(q1.size() >= k) {
                q2.push(q1.top()), q1.pop();
            }
            printf("%d\n", q2.top());
            q1.push(q2.top()), q2.pop(); //保证大根堆中元素数量等于k个
        }
    }
}

相关问题

洛谷P1801 黑匣子