单调队列求解滑动窗口最值：旅行问题

题目描述

John 打算驾驶一辆汽车周游一个环形公路。

公路上总共有 n 个车站，每站都有若干升汽油（有的站可能油量为零），每升油可以让汽车行驶一千米。

John 必须从某个车站出发，一直按顺时针（或逆时针）方向走遍所有的车站，并回到起点。

在一开始的时候，汽车内油量为零，John 每到一个车站就把该站所有的油都带上（起点站亦是如此），行驶过程中不能出现没有油的情况。

任务：判断以每个车站为起点能否按条件成功周游一周。

输入格式

第一行是一个整数 $n$，表示环形公路上的车站数；

接下来 $n$ 行，每行两个整数 $p_i$,$d_i$，分别表示表示第 $i$ 号车站的存油量和第 $i$ 号车站到 顺时针方向 下一站的距离。

输出格式

输出共 $n$ 行，如果从第 $i$ 号车站出发，一直按顺时针（或逆时针）方向行驶，能够成功周游一圈，则在第 $i$ 行输出 TAK，否则输出 NIE。

数据范围

$3\le n\le 10^6$,
$0\le p_i\le 2\times 10^9$,
$0\le d^i\le 2\times 10^9$

输入样例

5
3 1
1 2
5 2
0 1
5 4

输出样例

TAK
NIE
TAK
NIE
TAK

算法思想

根据问题描述，周游一个环形公路，一共有n个车站，如下图所示：

为了判断以每个车站为起点能否按条件成功周游一周，可以拆环为链地考虑每个起点i能否到达终点i + n。

从第 i 号车站出发时可以一直按顺时针（或逆时针）方向行驶，不妨以顺时针为例。假设以i点作为起点，i + n点作为终点，j为 i 点到 i + n 点中的任意一点。如果i到j经过所有点的油量p和距离d之差的和都大于等于0，说明从i能够成功到达j。即以i点作为起点，i + n点作为终点能够成功到达的充分必要条件就是，其中经过的每一点的 p - d 的前缀和都 ≥ 0，即s[j] - s[i - 1] >= 0。

这样，只需要保证其中最小的区间和min{s[j]−s[i−1]}≥0min\{s[j] - s[i - 1]\}\ge0min{s[j]−s[i−1]}≥0，由于起点$i$是固定的，所以只需要找到一个最小$s[j]$即可。这当于求一个区间长度为$n$的滑动窗口的最小值，可以使用单调队列实现。

注意：

• 需要顺时针和逆时针分别求解，有一种情况满足，即能够成功周游一圈。
• 顺时针求解时，求min{s[j]−s[i−1]}min\{s[j] - s[i - 1]\}min{s[j]−s[i−1]}，即最小$s[j]$
  
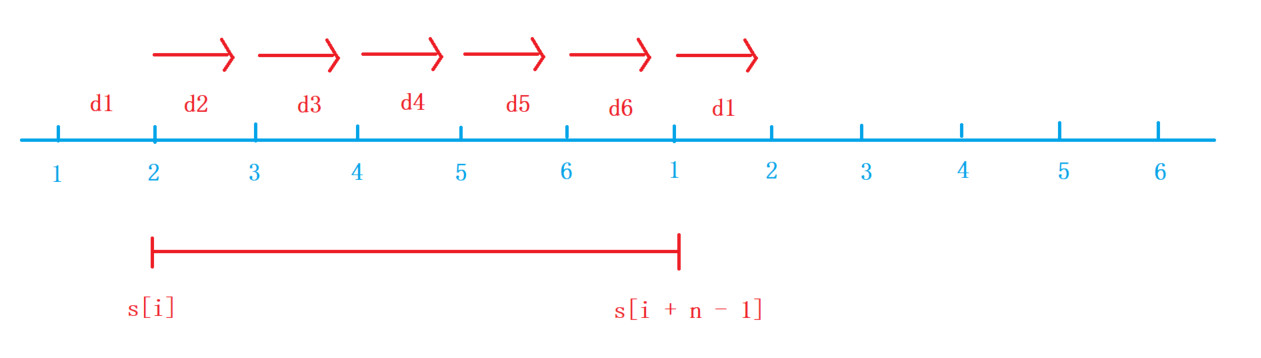
  • 前缀和s[i] = s[i - 1] + o[i] - d[i]
  • 要求出起点到后面 一段区间$[n+1,2\ast n]$ 中的最小值，只有从后往前处理才能在计算到当前数的时候，得到后面数的最小值。
• 逆时针求解时，求min{s[i]−s[j]}min\{s[i] - s[j]\}min{s[i]−s[j]}，即最大$s[j]$
  
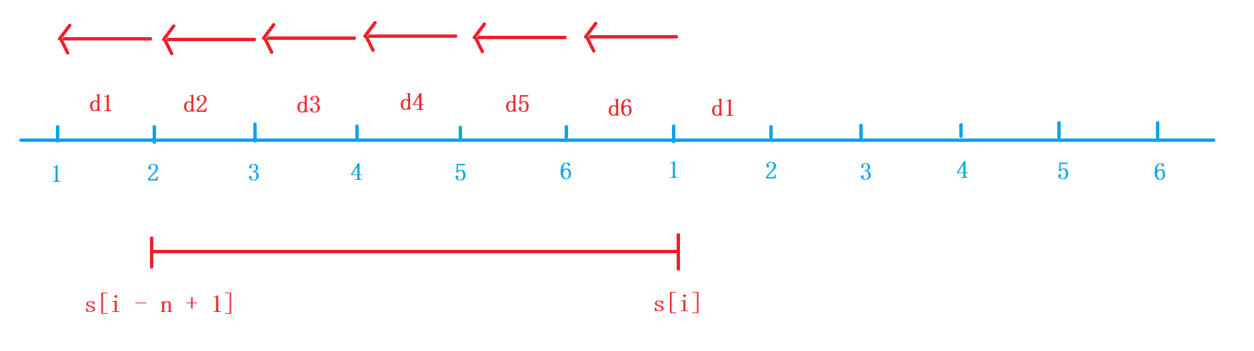
  • 前缀和s[i] = s[i - 1] + o[i] - d[i - 1]，其中d[0] = d[n]
  • 求出 前面 一段区间$[1,n]$ 中的最大值，只有从前往后处理才能在计算当前数的时候，得到前面数的最大值。

时间复杂度

$O(n)$

代码实现

#include <iostream>
#include <cstdio>
using namespace std;
typedef long long LL;
const int N = 2 * 1e6 + 10;
int p[N], d[N];
int q[N];
//s[i]前缀和数组
LL s[N];
//st[i]表示从i点出发能否绕行一圈
bool st[N];

int main()
{
    int n;
    scanf("%d", &n);
    for(int i = 1; i <= n; i ++) scanf("%d%d", &p[i], &d[i]);
    
    //顺时针处理前缀和
    for(int i = 1; i <= n; i ++) s[i] = s[n + i] = p[i] - d[i];
    for(int i = 1; i <= 2 * n; i ++) s[i] += s[i - 1];
    
    int hh = 0, tt = -1;
    //顺时针从后向前处理
    for(int i = 2 * n; i >= 1; i --)
    {
        //检查是否滑出窗口
        if(hh <= tt && q[hh] - i > n) hh ++;
        
        //将单调上升队列中队尾大于当前位置的元素全部出队
        while(hh <= tt && s[q[tt]] >= s[i]) tt --;
        q[++ tt] = i;
        
        //合法起点，并且最小区间和大于等于0
        if(i <= n && s[q[hh]] - s[i - 1] >= 0) st[i] = 1;
    }
    
    //逆时针处理前缀和
    d[0] = d[n];
    for(int i = 1; i <= n; i ++) s[i] = s[n + i] = p[i] - d[i - 1];
    for(int i = 1; i <= 2 * n; i ++) s[i] += s[i - 1];
    
    hh = 0, tt = -1;
    //顺时针从前向后处理
    for(int i = 1; i <= 2 * n; i ++)
    {
         //检查是否滑出窗口
         if(hh <= tt && i - q[hh] > n) hh ++;
         
         //将单调下降队列中队尾小于当前位置的元素全部出队
         while(hh <= tt && s[q[tt]] <= s[i]) tt --;
         q[++ tt] = i;
         
         //合法起点，并且最小区间和大于等于0
         if(i > n && s[i] - s[q[hh]] >= 0) st[i - n] = 1;
    }
        
    for(int i = 1; i <= n; i++)
        if(st[i]) puts("TAK");
        else puts("NIE");
        
    return 0;
}