两个字符串间的最短路径问题

题目解析

本题可以通过动态规划来求解：

我们假设dp[i][j]表示(0,0)到(i,j)的最短距离，那么这个最短距离只可能来自三个方向：

• dp[i-1][j]，当前点的上方点
• dp[i][j-1]，当前点的左边点
• dp[i-1][j-1]，当前点的左上方点

而存在推导式如下：

dp[i][j] = min(dp[i-1][j]，dp[i][j-1]，dp[i-1][j-1]) + 1

另外需要注意的是，上面推导式dp[i-1][j-1]参与比较是有前提条件的，即如果(i-1, j-1)点和(i,j)点之间存在斜线相连时，才能将dp[i-1][j-1]带入上面推导式，否则不能带入。

并且上面推导式还可以优化，如果当前点可以向三个方向扩散：

• 向右
• 向下
• 向右下

那么向右和向下是否有必要扩散呢？比如下图

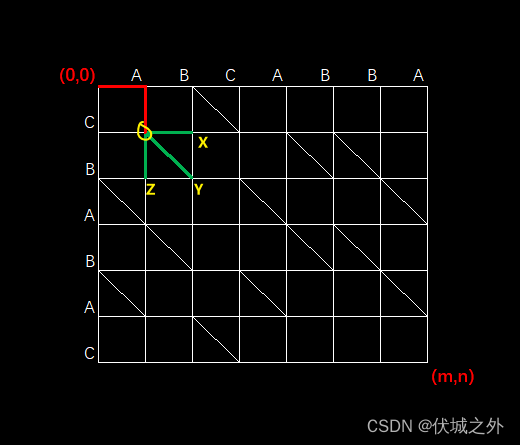
从(1,1)处可以向三个方向扩散，此时可以看出扩散后的三个新位置X,Y,Z，其中Y要比X,Z更靠近右下角点。

那么有没