【课程表】

题目来源

207. 课程表 - 力扣（LeetCode）

我们可以根据题目要求画出一个有向图，比如下面用例

numCourses = 4, prerequisites = [[2,1], [4,3], [4,2]]

学2之前，必须先学1；

学4之前，必须先学2，3

学1，3没有前置课程。

因此，通过上面有向图，我们可以得出，能够学完所有课程。

而上面有向图其实就是一种拓扑结构，在拓扑结构中，每一个顶点都有“入度”概念，所谓入度，即当前顶点的直接前驱顶点数目

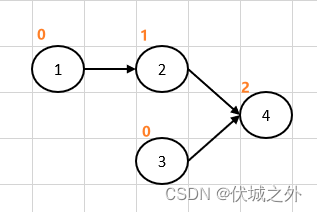
如上图所示，

顶点1的入度为0

顶点2的入度为1

顶点3的入度为0

顶点4的入度为2，注意入度指的是当前顶点的直接前驱顶