安排新同学到空位

题目描述

新学期开始了，班级来了一些新同学，刚好教室中某一排存在一些空位。

请帮忙将安排新同学到空位上，使得学生不要过于分散，即需要形成一个最长连续非空位。

输入描述

第一行输入一个数列，用于描述座位的使用情况，数列元素 0 表示空位，1 表示已占位。数列元素之间以空格分隔。最多1000000个座位。

第二行输入新同学的数量。用例保证新同学数量不超过空位。

输出描述

输出两个整数，分别表示新同学入座后，形成的最长连续非空位的起始位置和长度，以空格分隔。

若存在多个这样的最长连续非空串，则起始位置最大的。

注意：起始位置从 1 开始计数。

用例

输入	1 0 1 1 0 1 1 0 1 1 1
输出	6 5
说明	无

题目解析

如下图中，红色数字表示空位的编号。现在我们有 K 个没座位的新同学，可以安排进这些空位中。

当 K == 1 时，即只有一个新同学，此时可以安排到任意一个红色空位上。安排后，可以生成更长的连续学生数量（黄色+绿色部分）。

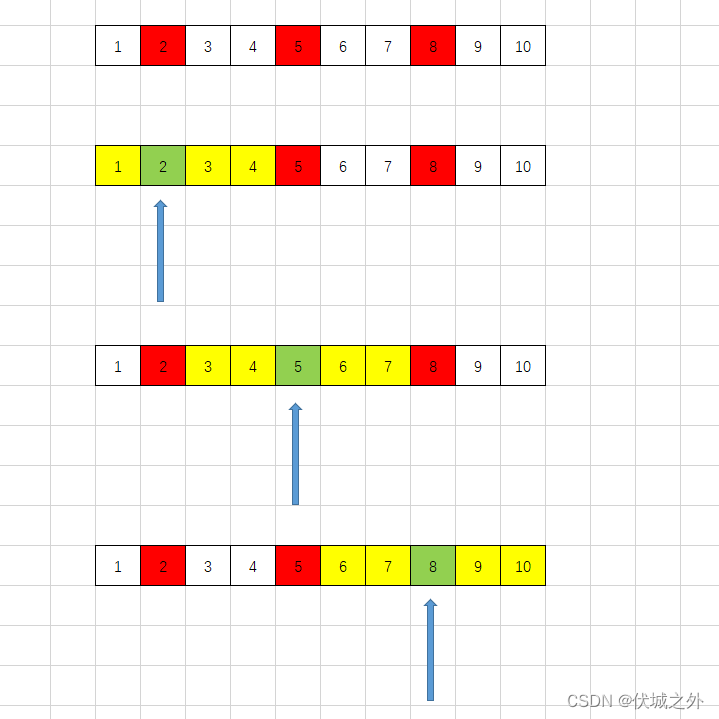
我们假设空座编号列表为 empty = [2,5,8]，那么：

• 当我们将唯一的新同学安排到 empty[0] 编号空位时，此时形成 [0, empty[1] - 1] 的连续学生范围
• 当我们将唯一的新同学安排到 empty[1] 编号空位时，此时形成 [empty[0] + 1, empty[2] - 1] 的连续学生范围
• 当我们将唯一的新同学安排到 empty[2] 编号空位时，此时形成 [empty[1] + 1, N] 的连续学生范围

再次抽象一下，假设我们将新同学安排到 empty[index] 空位时，那么：

• 若 index == 0，则形成的连续学生范围的左边界可以到 1，右边界是 empty[index+1] - 1
• 若 index == empty.length - 1，则形成的连续学生范围右边界可以到 N，左边界是 empty[index-1]+1
• 若 0 < index < empty.length - 1，则形成的连续学生范围是 [empty[index-1] + 1, empty[index+1] - 1]

再次抽象一下，假设我们新加入同学数量 K >1 呢？

• 从 empty[0] 开始坐，形成连续学生范围是：

1. 开始编号：1
2. 结束编号：empty[0+k] - 1
3. 长度：（empty[0+k] - 1）- 1 + 1

• 从empty[m-k] 开始坐，形成连续学生范围是：

1. 开始编号：empty[m-k-1] + 1
2. 结束编号：n
3. 长度：n - (empty[m-k-1] + 1) + 1

• 如果从其余 empty[i] 开始补种，此时连续胡杨树的：

1. 开始编号：empty[i-1] + 1
2. 结束编号：empty[i+k] - 1
3. 长度：(empty[i + k] - 1) - (empty[i-1] + 1) + 1 

JS算法源码

const rl = require("readline").createInterface({ input: process.stdin });
var iter = rl[Symbol.asyncIterator]();
const readline = async () => (await iter.next()).value;

void (async function () {
  // 座位使用情况
  const seats = (await readline()).split(" ").map(Number);

  // 总座位数量
  const n = seats.length;

  // 记录空位编号
  const empty = [];
  for (let i = 0; i < n; i++) {
    if (seats[i] == 0) {
      empty.push(i + 1);
    }
  }

  // 空位数量
  const m = empty.length;

  // 新同学数量
  const k = parseInt(await readline());

  // 如果空位数量m 等于 新同学数量 k，则可以坐满一排，即最长连续学生数为 n, 起始位置位1
  if (m == k) {
    return console.log(1 + " " + n);
  }

  // 下面逻辑请看题目解析推导过程
  let maxLen = 0;
  let maxLen_start = -1;

  for (let i = 0; i <= m - k; i++) {
    let start, end;

    switch (i) {
      case 0:
        start = 1;
        end = empty[i + k] - 1;
        break;
      case m - k:
        start = empty[i - 1] + 1;
        end = n;
        break;
      default:
        start = empty[i - 1] + 1;
        end = empty[i + k] - 1;
    }

    const len = end - start + 1;

    if (len >= maxLen) {
      maxLen = len;
      maxLen_start = start;
    }
  }

  console.log(`${maxLen_start} ${maxLen}`);
})();

Java算法源码

import java.util.ArrayList;
import java.util.Arrays;
import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);

        // 座位使用情况
        int[] seats = Arrays.stream(sc.nextLine().split(" ")).mapToInt(Integer::parseInt).toArray();

        // 总座位数量
        int n = seats.length;

        // 记录空位编号
        ArrayList<Integer> empty = new ArrayList<>();
        for (int i = 0; i < n; i++) {
            if (seats[i] == 0) {
                empty.add(i + 1);
            }
        }

        // 空位数量
        int m = empty.size();

        // 新同学数量
        int k = sc.nextInt();

        // 如果空位数量m 等于 新同学数量 k，则可以坐满一排，即最长连续学生数为 n
        if (m == k) {
            System.out.println(1 + " " + n);
            return;
        }

        // 下面逻辑请看题目解析推导过程
        int maxLen = 0;
        int maxLen_start = -1;

        for (int i = 0; i <= m - k; i++) {
            int start, end;

            if (i == 0) {
                start = 1;
                end = empty.get(i + k) - 1;
            } else if (i == m - k) {
                start = empty.get(i - 1) + 1;
                end = n;
            } else {
                start = empty.get(i - 1) + 1;
                end = empty.get(i + k) - 1;
            }

            int len = end - start + 1;

            if (len >= maxLen) {
                maxLen = len;
                maxLen_start = start;
            }
        }

        System.out.println(maxLen_start + " " + maxLen);
    }
}

Python算法源码

if __name__ == '__main__':
    # 座位使用情况
    seats = list(map(int, input().split()))

    # 总座位数量
    n = len(seats)

    # 记录空位编号
    empty = []
    for i in range(n):
        if seats[i] == 0:
            empty.append(i + 1)

    # 空位数量
    m = len(empty)

    # 新同学数量
    k = int(input())

    # 如果空位数量m 等于 新同学数量 k，则可以坐满一排，即最长连续学生数为 n
    if m == k:
        print(f"{1} {n}")
        exit()

    # 下面逻辑请看题目解析推导过程
    maxLen = 0
    maxLen_start = -1

    for i in range(m - k + 1):
        if i == 0:
            start, end = 1, empty[i + k] - 1
        elif i == m - k:
            start, end = empty[i - 1] + 1, n
        else:
            start, end = empty[i - 1] + 1, empty[i + k] - 1

        length = end - start + 1

        if length >= maxLen:
            maxLen = length
            maxLen_start = start

    print(f"{maxLen_start} {maxLen}")

C算法源码

#include <stdio.h>

#define MAX_LEN 1000000

int seats[MAX_LEN]; // 座位使用情况
int empty[MAX_LEN]; // 记录空位编号

int main() {
    int n = 0; // 总座位数量
    while (scanf("%d", &seats[n++])) {
        if (getchar() != ' ') break;
    }

    int m = 0; // 空位数量
    for (int i = 0; i < n; i++) {
        if (seats[i] == 0) {
            empty[m++] = i + 1;
        }
    }

    // 新同学数量
    int k;
    scanf("%d", &k);

    // 如果空位数量m 等于 新同学数量 k，则可以坐满一排，即最长连续学生数为 n
    if (m == k) {
        printf("%d %d", 1, n);
        return 0;
    }

    // 下面逻辑请看题目解析推导过程
    int maxLen = 0;
    int maxLen_start = -1;

    for (int i = 0; i <= m - k; i++) {
        int start, end;

        if (i == 0) {
            start = 1;
            end = empty[i + k] - 1;
        } else if (i == m - k) {
            start = empty[i - 1] + 1;
            end = n;
        } else {
            start = empty[i - 1] + 1;
            end = empty[i + k] - 1;
        }

        int len = end - start + 1;

        if (len >= maxLen) {
            maxLen = len;
            maxLen_start = start;
        }
    }

    printf("%d %d", maxLen_start, maxLen);

    return 0;
}

C++算法源码

#include <bits/stdc++.h>

using namespace std;

int main() {
    vector<int> seats; // 座位使用情况

    int v;
    while (cin >> v) {
        seats.emplace_back(v);
        if (getchar() != ' ') break;
    }

    int n = seats.size();  // 总座位数量

    vector<int> empty; // 记录空位编号
    for (int i = 0; i < n; i++) {
        if (seats[i] == 0) {
            empty.emplace_back(i + 1);
        }
    }

    int m = empty.size(); // 空位数量

    // 新同学数量
    int k;
    cin >> k;

    // 如果空位数量m 等于 新同学数量 k，则可以坐满一排，即最长连续学生数为 n
    if (m == k) {
        cout << 1 << " " << n;
        return 0;
    }

    // 下面逻辑请看题目解析推导过程
    int maxLen = 0;
    int maxLen_start = -1;

    for (int i = 0; i <= m - k; i++) {
        int start, end;

        if (i == 0) {
            start = 1;
            end = empty[i + k] - 1;
        } else if (i == m - k) {
            start = empty[i - 1] + 1;
            end = n;
        } else {
            start = empty[i - 1] + 1;
            end = empty[i + k] - 1;
        }

        int len = end - start + 1;

        if (len >= maxLen) {
            maxLen = len;
            maxLen_start = start;
        }
    }

    cout << maxLen_start << " " << maxLen << endl;

    return 0;
}