好久没发题解了,先发一道水题题解。
这个题跟poj3279类似,比那个简单一些,棋盘大小只有4*4,但是做法类似,都是穷举第一行的2^n种可能,然后根据每种状态贪心的得出相应状态,最后判断最后一行。但是这个题是翻成黑的白的都行,所以要讨论两种情况,注意一下就好。
Flip Game
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 35127 | Accepted: 15374 |
Description
Flip game is played on a rectangular 4x4 field with two-sided pieces placed on each of its 16 squares. One side of each piece is white and the other one is black and each piece is lying either it's black or white side up. Each round you flip 3 to 5 pieces, thus changing the color of their upper side from black to white and vice versa. The pieces to be flipped are chosen every round according to the following rules:
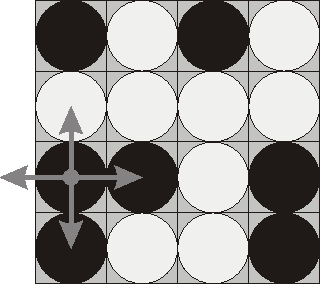 Consider the following position as an example:
Consider the following position as an example:
bwbw
wwww
bbwb
bwwb
Here "b" denotes pieces lying their black side up and "w" denotes pieces lying their white side up. If we choose to flip the 1st piece from the 3rd row (this choice is shown at the picture), then the field will become:
bwbw
bwww
wwwb
wwwb
The goal of the game is to flip either all pieces white side up or all pieces black side up. You are to write a program that will search for the minimum number of rounds needed to achieve this goal.
- Choose any one of the 16 pieces.
- Flip the chosen piece and also all adjacent pieces to the left, to the right, to the top, and to the bottom of the chosen piece (if there are any).
 Consider the following position as an example:
Consider the following position as an example:
bwbw
wwww
bbwb
bwwb
Here "b" denotes pieces lying their black side up and "w" denotes pieces lying their white side up. If we choose to flip the 1st piece from the 3rd row (this choice is shown at the picture), then the field will become:
bwbw
bwww
wwwb
wwwb
The goal of the game is to flip either all pieces white side up or all pieces black side up. You are to write a program that will search for the minimum number of rounds needed to achieve this goal.
Input
The input consists of 4 lines with 4 characters "w" or "b" each that denote game field position.
Output
Write to the output file a single integer number - the minimum number of rounds needed to achieve the goal of the game from the given position. If the goal is initially achieved, then write 0. If it's impossible to achieve the goal, then write the word "Impossible" (without quotes).
Sample Input
bwwb bbwb bwwb bwww
Sample Output
4
Source
#include <iostream>
#include <stdio.h>
#include <math.h>
#include <stdlib.h>
#include <string>
#include <string.h>
#include <algorithm>
#include <vector>
#include <queue>
#include <set>
#include <map>
#include <stack>
using namespace std;
typedef long long LL;
const int INF=0x7fffffff;
const int MAX_N=10000;
int F[4][4];
int newf1[4][4];
int newf2[4][4];
char a;
int d[4][2]={1,0,0,1,0,-1,-1,0};
bool inF(int x,int y){
return x>=0&&x<4&&y>=0&&y<4;
}
void turn(int x,int y,int p[4][4]){
for(int i=0;i<4;i++){
int nx=x+d[i][0];
int ny=y+d[i][1];
if(inF(nx,ny)){
p[nx][ny]++;
p[nx][ny]%=2;
}
}
p[x][y]++;
p[x][y]%=2;
}
int main(){
int ans=INF;
for(int i=0;i<4;i++){
for(int j=0;j<4;j++){
scanf(" %c",&a);
if(a=='b')F[i][j]=1;
else F[i][j]=0;
}//黑的是1,白的是0
}
int sum1=0,sum2=0;
for(int i=0;i<16;i++){
memset(newf1,0,sizeof(newf1));
memset(newf2,0,sizeof(newf2));
sum1=0;
sum2=0;
memcpy(newf1,F,sizeof(F));
memcpy(newf2,F,sizeof(F));
for(int j=4;j>=1;j--){
if((i>>(4-j))&1){
turn(0,j-1,newf1);
turn(0,j-1,newf2);
sum1++;
sum2++;
}
}
// cout<<endl;
for(int j=1;j<4;j++){
for(int k=0;k<4;k++){
if(newf1[j-1][k]==0){
turn(j,k,newf1);
sum1++;
}
if(newf2[j-1][k]==1){
turn(j,k,newf2);
sum2++;
}
}
}
for(int j=0;j<4;j++){
if(newf1[3][j]==0){
sum1=INF;
break;
}
}
for(int j=0;j<4;j++){
if(newf2[3][j]==1){
sum2=INF;
break;
}
}
// cout<<sum1<<" "<<sum2<<endl;
ans=min(min(sum1,ans),sum2);
// cout<<sum<<endl;
}
if(ans==INF)cout<<"Impossible"<<endl;
else cout<<ans<<endl;
return 0;
}

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








