一维正态分布
设 X ~ N ( μ , σ 2 ) X\text{\large\textasciitilde}N(\mu,\sigma^2) X~N(μ,σ2),则 X X X的概率密度为 f ( x ) = 1 2 π σ e − ( x − μ ) 2 2 σ 2 f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}} f(x)=2πσ1e−2σ2(x−μ)2函数图像:钟形曲线, x = μ x=\mu x=μ为对称轴且为最大值点,最大值为 1 2 π σ \frac{1}{\sqrt{2\pi}\sigma} 2πσ1, σ \sigma σ越小图像越尖锐。
- μ = 1 , σ = 1 \mu=1,\sigma=1 μ=1,σ=1:

- μ = 0 , σ = 1 2 \mu=0,\sigma=\frac{1}{2} μ=0,σ=21:
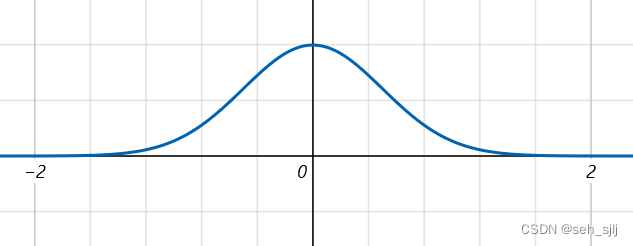
- μ = 0 , σ ∈ ( 0 , 5 ] \mu=0,\sigma\in(0,5] μ=0,σ∈(0,5]:
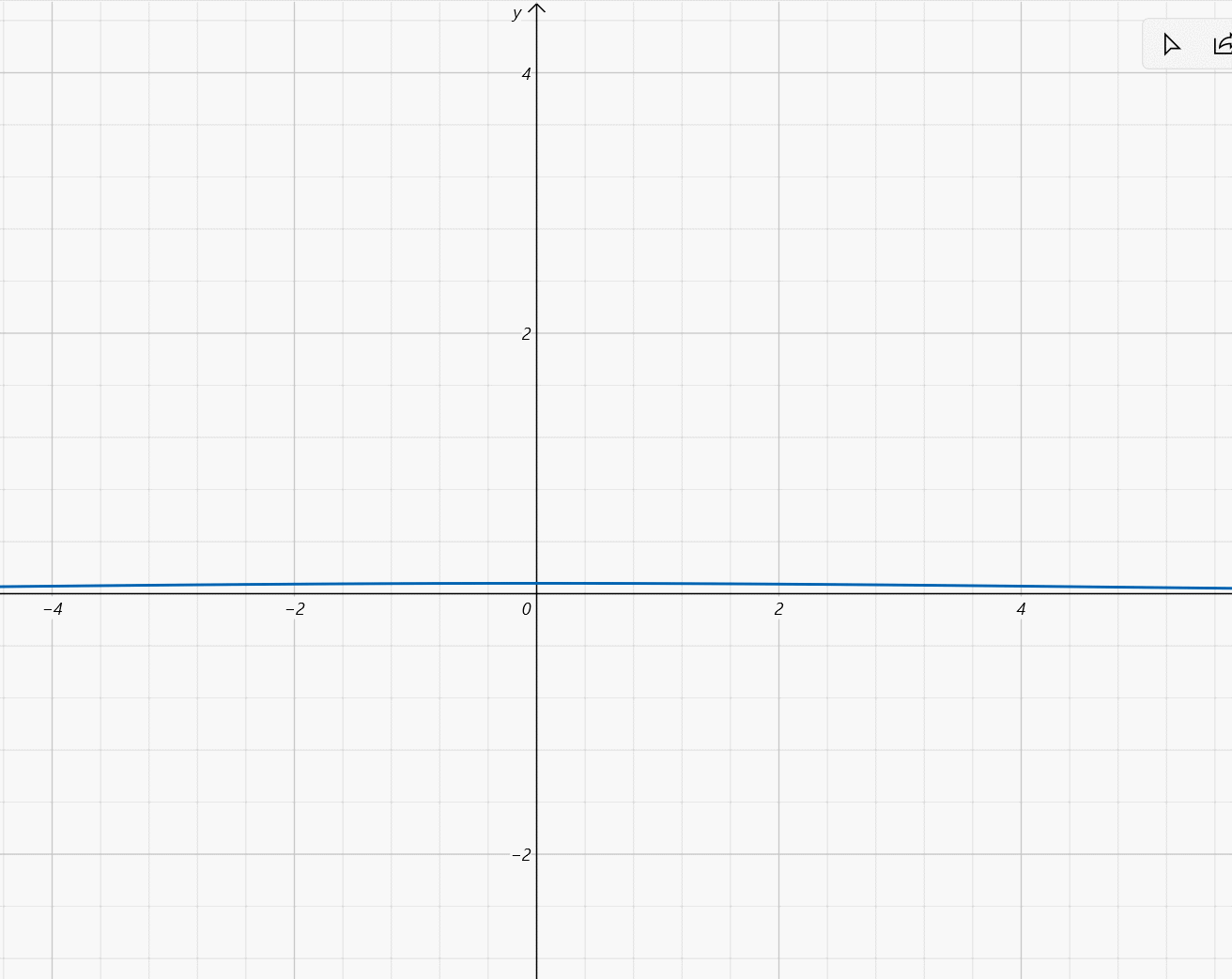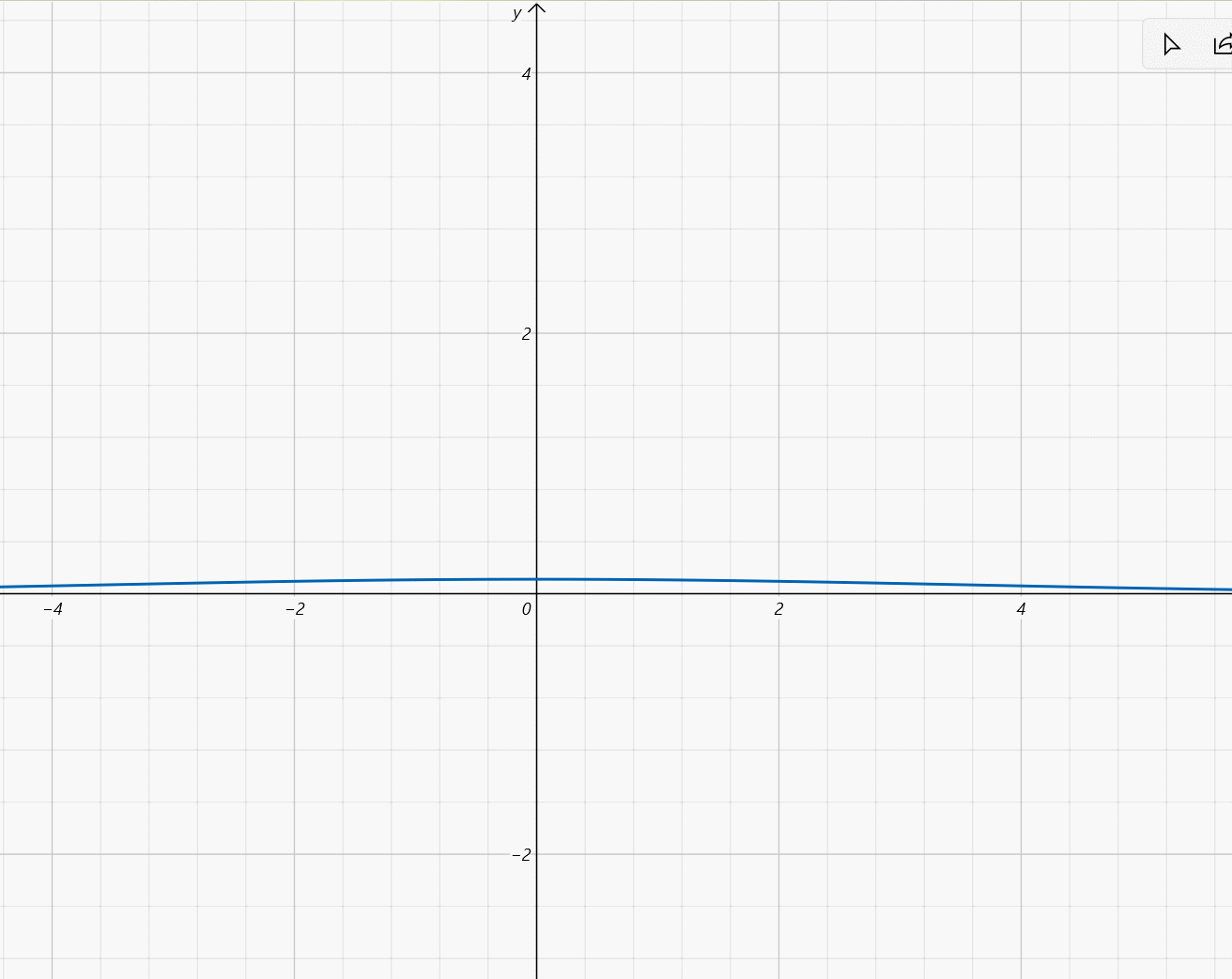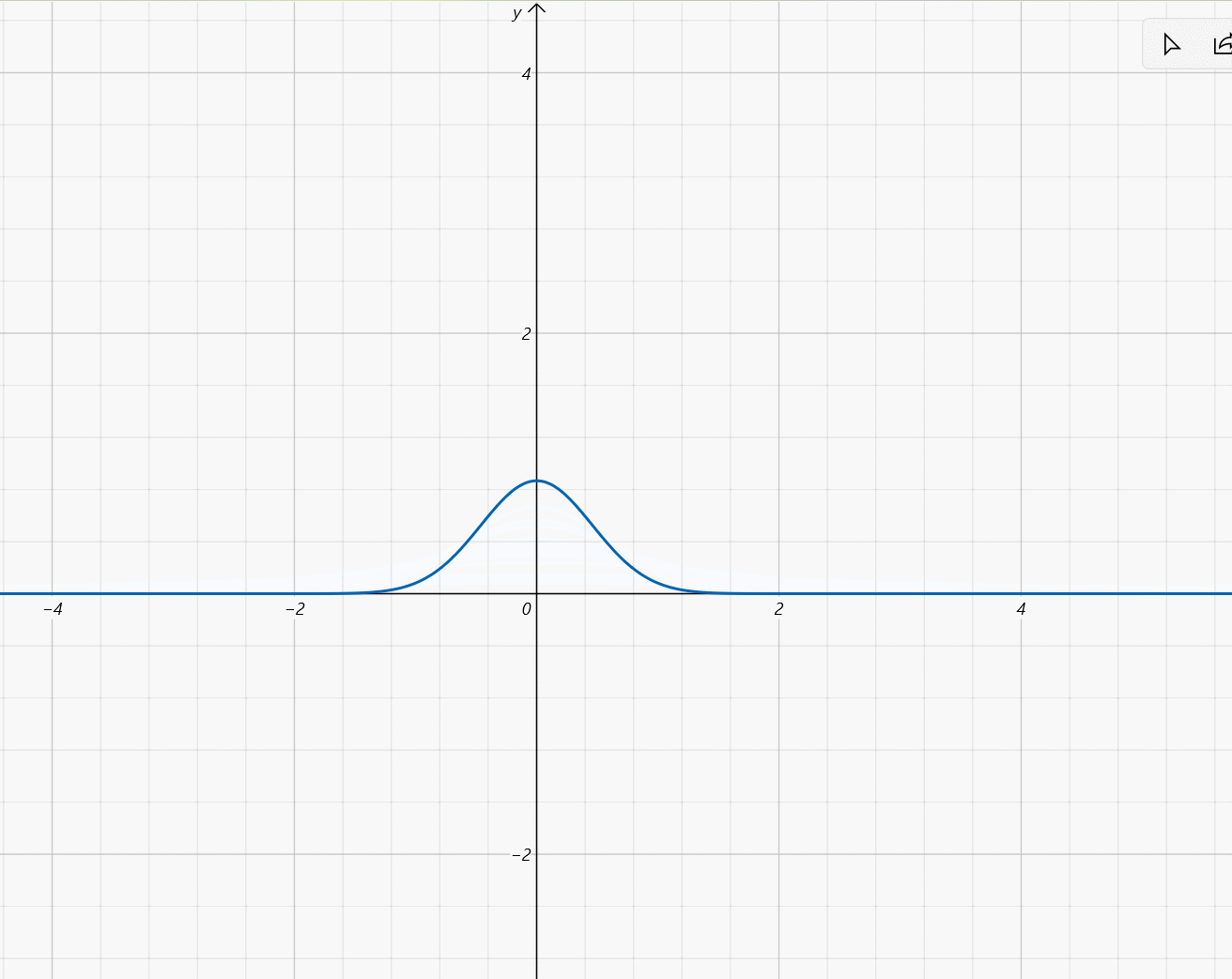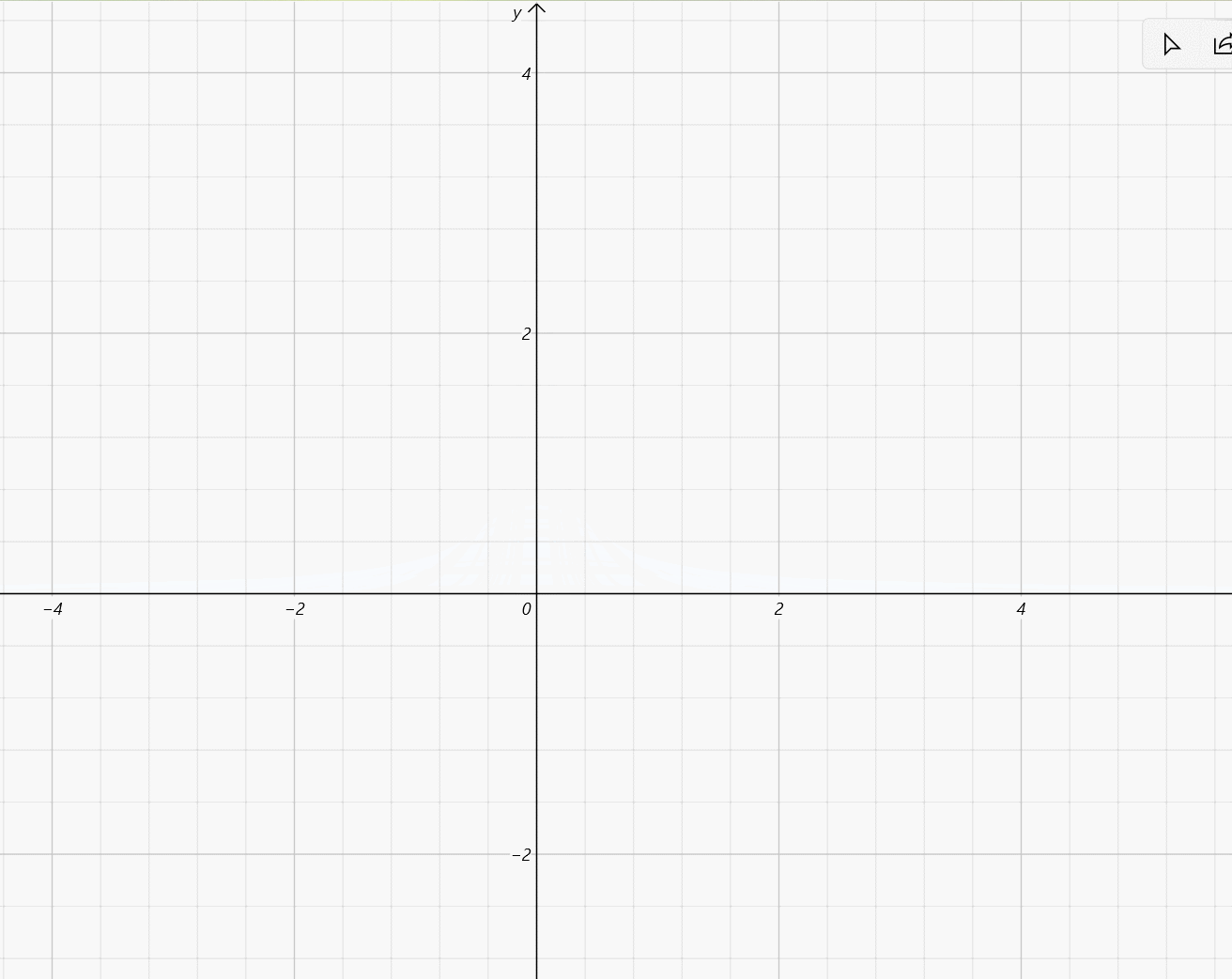
- μ ∈ [ − 2 , 2 ] , σ = 1 5 \mu\in[-2,2],\sigma=\frac{1}{5} μ∈[−2,2],σ=51:
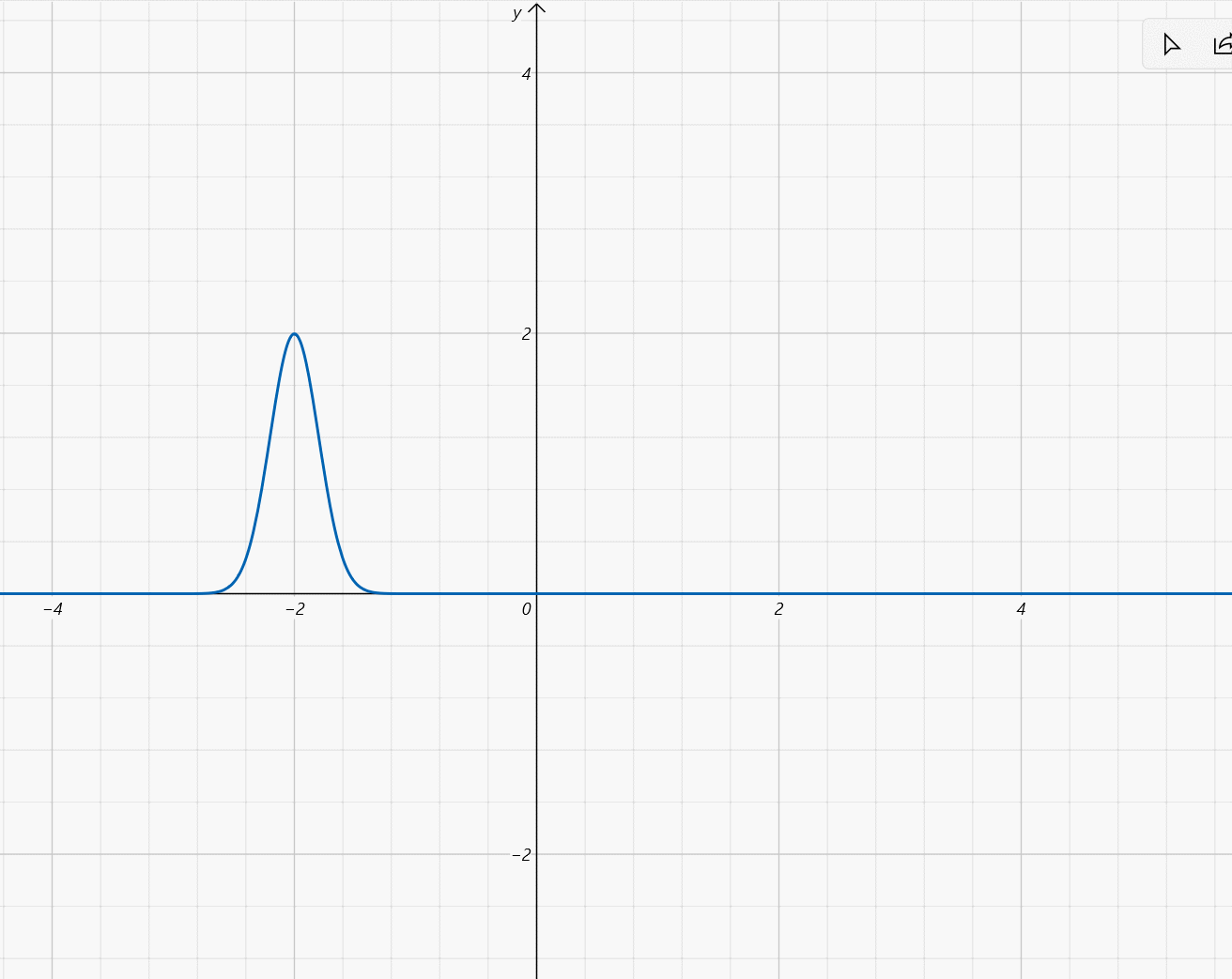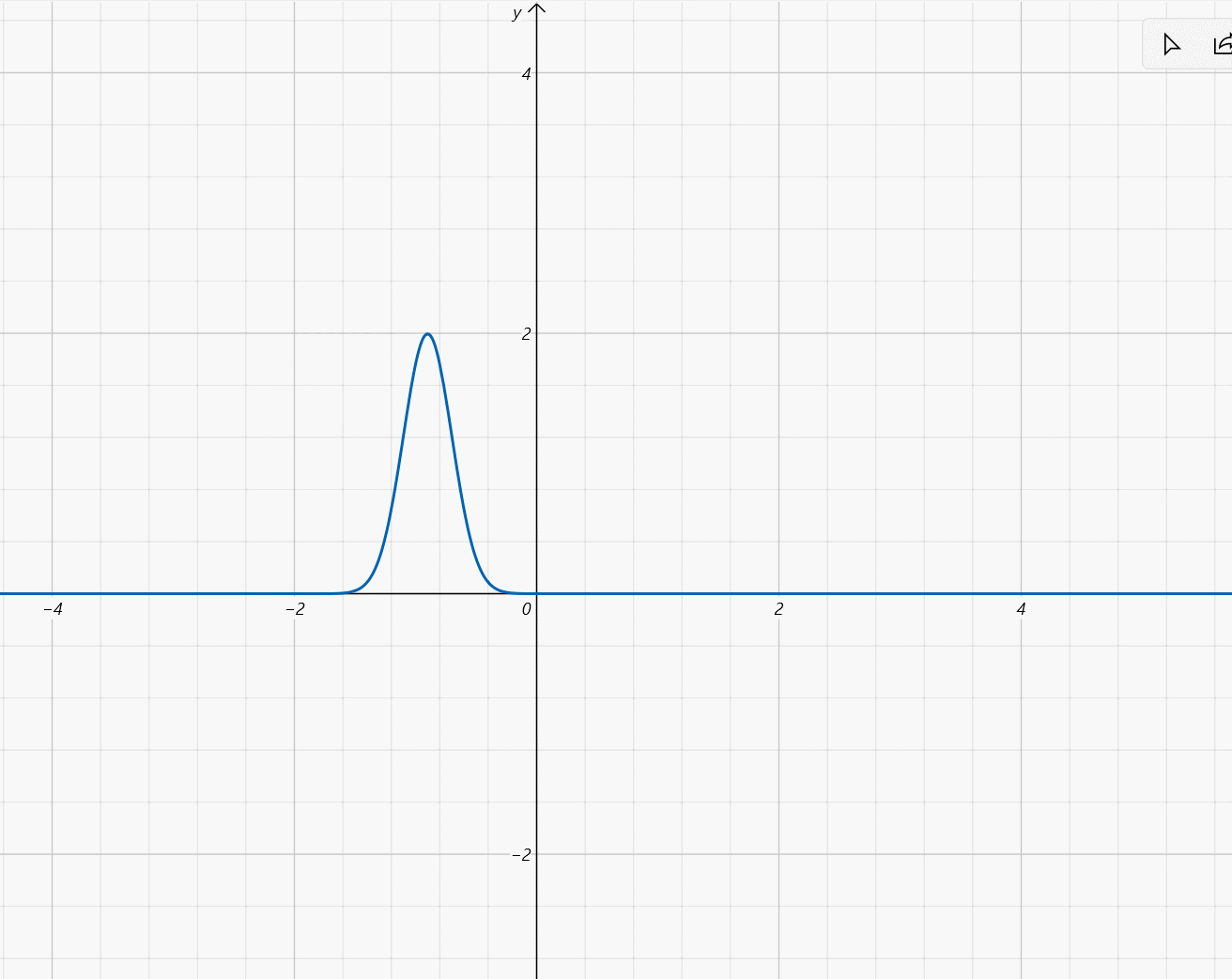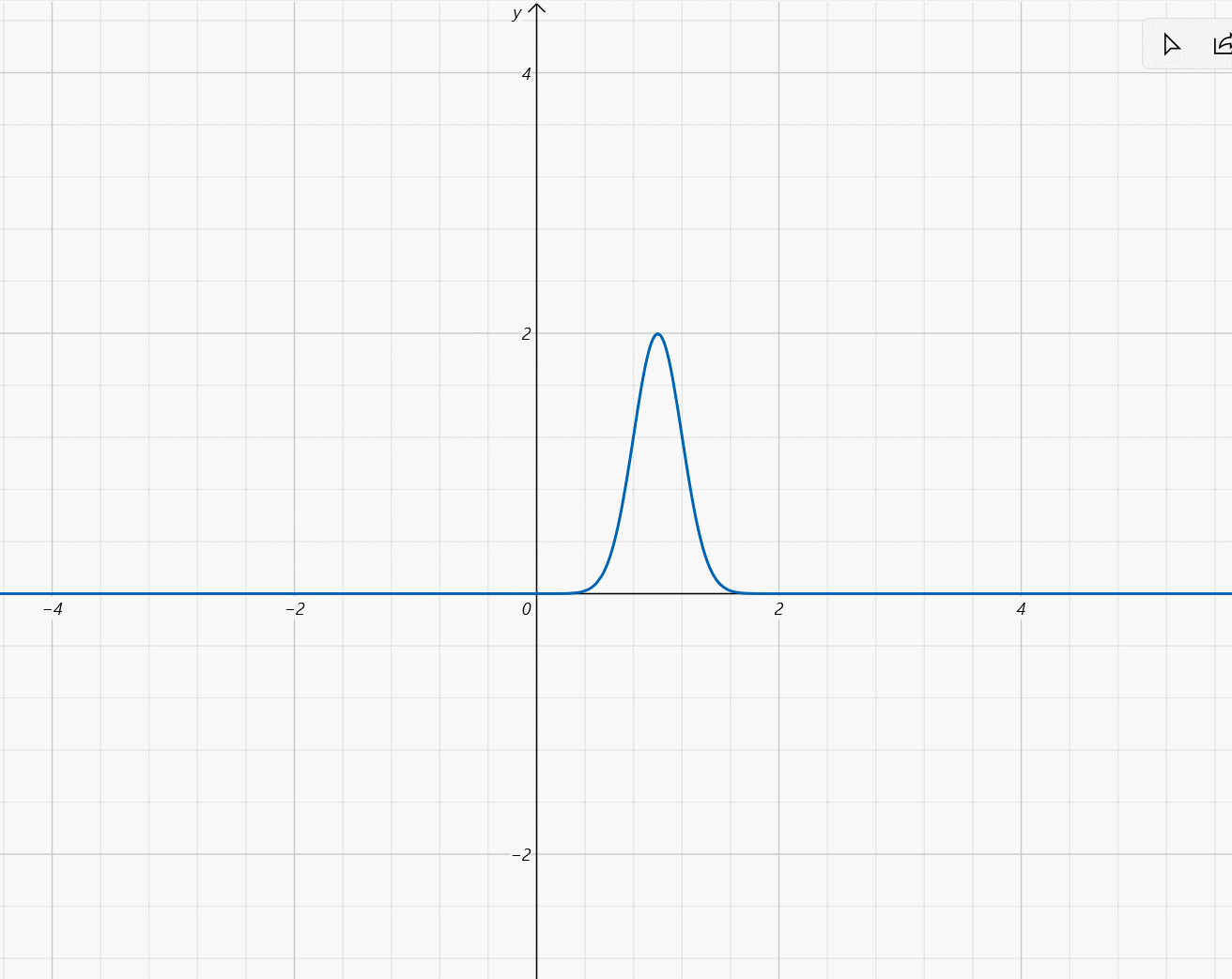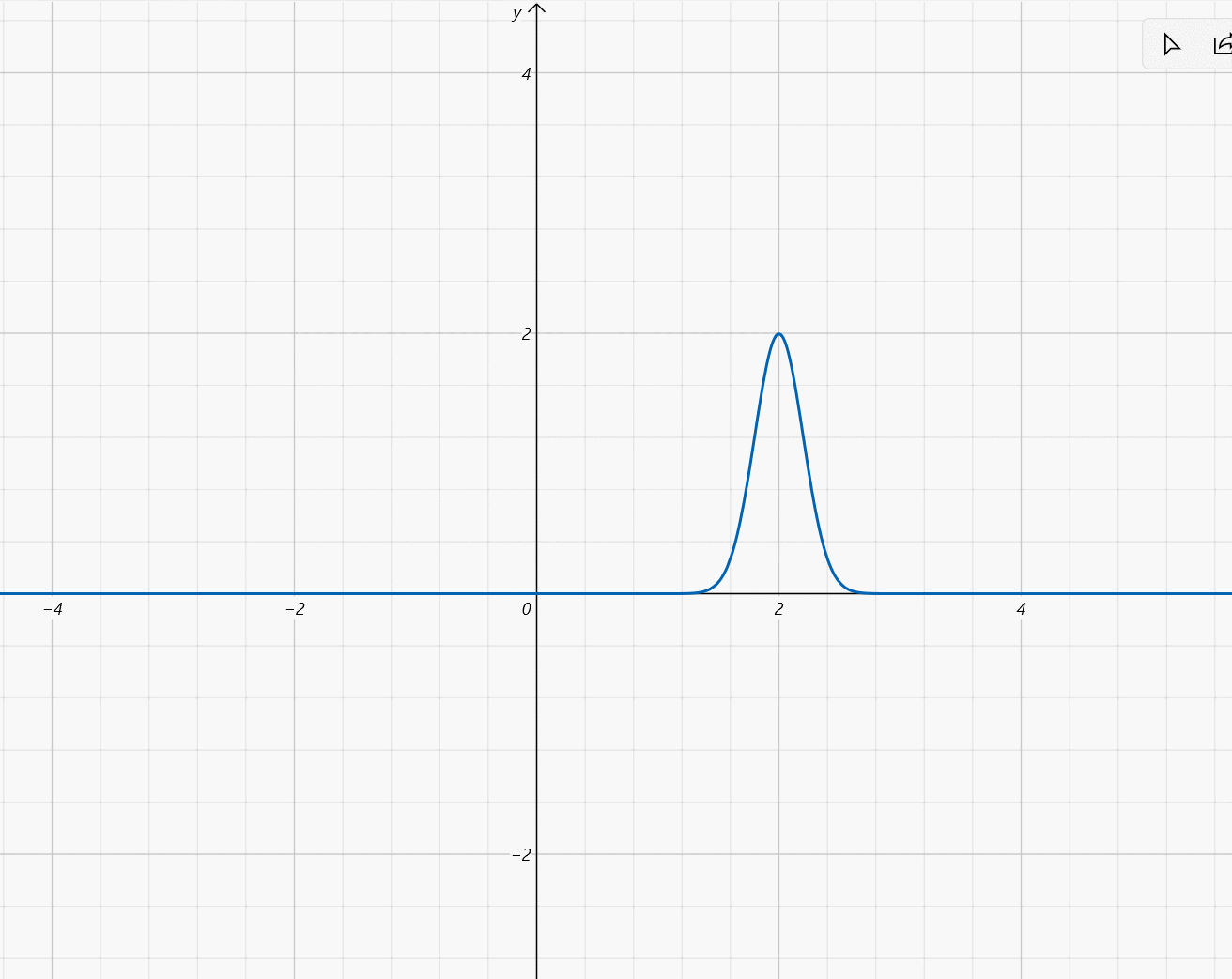
标准正态分布 N ( 0 , 1 ) N(0,1) N(0,1):设 X ~ N ( 0 , 1 ) X\text{\large\textasciitilde}N(0,1) X~N(0,1),则 X X X的概率密度函数记作 ϕ ( x ) = 1 2 π e − x 2 2 \phi(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}} ϕ(x)=2π1e−2x2 X X X的分布函数记作 Φ ( x ) \Phi(x) Φ(x),满足 Φ ( 0 ) = 1 2 , Φ ( − x ) = 1 − Φ ( x ) \Phi(0)=\frac{1}{2},\quad\Phi(-x)=1-\Phi(x) Φ(0)=21,Φ(−x)=1−Φ(x)若 X ~ N ( μ , σ 2 ) X\text{\large\textasciitilde}N(\mu,\sigma^2) X~N(μ,σ2),则 Z = X − μ σ ~ N ( 0 , 1 ) Z=\frac{X-\mu}{\sigma}\text{\large\textasciitilde}N(0,1) Z=σX−μ~N(0,1)。
X ~ N ( μ , σ 2 ) ⟹ Y = k X + b ~ N ( k μ + b , k 2 σ 2 ) X\text{\large\textasciitilde}N(\mu,\sigma^2)\implies Y=kX+b\,\text{\large\textasciitilde}\,N(k\mu+b,k^2\sigma^2) X~N(μ,σ2)⟹Y=kX+b~N(kμ+b,k2σ2)(其中 b ≠ 0 b\ne0 b=0)
X ~ N ( μ , σ 2 ) ⟹ E ( X ) = μ , D ( X ) = σ 2 , σ ( x ) = σ X\text{\large\textasciitilde}N(\mu,\sigma^2)\implies E(X)=\mu,\ D(X)=\sigma^2,\ \sigma(x)=\sigma X~N(μ,σ2)⟹E(X)=μ, D(X)=σ2, σ(x)=σ
中心极限定理:
| 中心极限定理 | 条件 | 结论(当 n n n足够大时近似成立) |
|---|---|---|
| 独立同分布中心极限定理 | 有有限的数学期望 E ( X k ) = μ E(X_k)=\mu E(Xk)=μ和方差 D ( X k ) = σ 2 ≠ 0 D(X_k)=\sigma^2\ne0 D(Xk)=σ2=0 | X ‾ ~ N ( μ , σ 2 n ) , ∑ k = 1 n X k ~ N ( n μ , n σ 2 ) \overline{X}\text{\large\textasciitilde}N\left(\mu,\frac{\sigma^2}{n}\right),\ \sum\limits_{k=1}^n X_k\text{\large\textasciitilde}N\left(n\mu,n\sigma^2\right) X~N(μ,nσ2), k=1∑nXk~N(nμ,nσ2) |
| 棣莫弗-拉普拉斯中心极限定理 | η n ~ B ( n , p ) \eta_n\text{\large\textasciitilde}B(n,p) ηn~B(n,p) | X ‾ ~ N ( p , p ( 1 − p ) n ) , η n ~ N ( n p , n p ( 1 − p ) ) \overline{X}\text{\large\textasciitilde}N\left(p,\frac{p(1-p)}{n}\right),\ \eta_n\text{\large\textasciitilde}N(np,np(1-p)) X |





 本文详细介绍了从一维到多维正态分布的概念、性质及应用。涵盖了中心极限定理、一维正态分布的概率密度函数及其特性、多维正态分布的概率密度函数形式及其基本性质等内容。
本文详细介绍了从一维到多维正态分布的概念、性质及应用。涵盖了中心极限定理、一维正态分布的概率密度函数及其特性、多维正态分布的概率密度函数形式及其基本性质等内容。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 8038
8038

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








