第十届蓝桥杯2019年C/C++ 大学B组省赛试题

试题A：组队

【问题描述】
作为篮球队教练，你需要从以下名单中选出 1号位至 5号位各一名球员，
组成球队的首发阵容。
每位球员担任 1号位至 5号位时的评分如下表所示。请你计算首发阵容 1
号位至5号位的评分之和最大可能是多少？

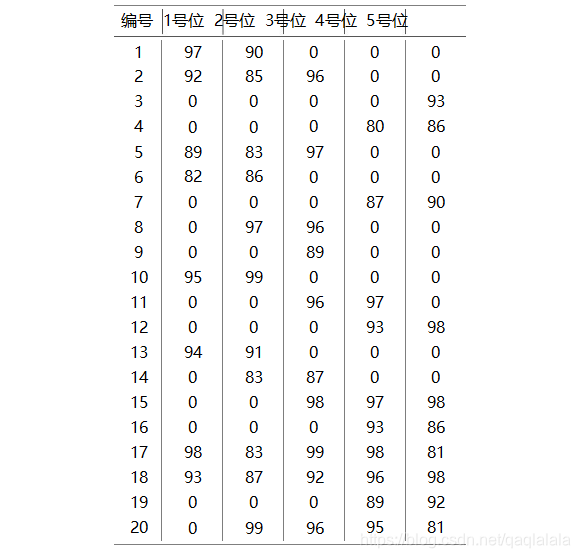
97+99+98+98+98 = 490

试题B： 年号字串

小明用字母 A对应数字 1，B对应 2，以此类推，用 Z对应 26。对于 27
以上的数字，小明用两位或更长位的字符串来对应，例如 AA对应27，AB对
应28，AZ对应52，LQ对应329。
请问2019对应的字符串是什么？

2019//26 = 77
77 // 26 = 2  B
2019%26 = 17  Q
B*Q
2019 = 17+x*26+26*26*2
x = Y

答案： BYQ

试题C： 数列求值

给定数列1,1,1,3,5,9,17,…，从第4项开始，每项都是前3项的和。求
第20190324项的最后4位数字。

a = 1
b = 1
c = 1
d = 0
for i in range(4,20190325):
    d = (a+b+c)%10000
    a = b
    b = c
    c = d
print(d)

答案：4659

试题D：数的分解

把 2019分解成 3个各不相同的正整数之和，并且要求每个正整数都不包
含数字2和4，一共有多少种不同的分解方法？
注意交换 3个整数的顺序被视为同一种方法，例如 1000+1001+18和
1001+1000+18被视为同一种

num = 0
for i in range(1,2019):
    for j in range(i+1,2019):
        k = 2019-i-j
        if i != j and i != k and j != k:
            if k < j or k < i:
                break
            a = str(i)+str(j)+str(k)
            if a.count('2') == 0 and a.count('4') == 0:
                num += 1
print(num)

答案：40785

试题E： 迷宫

试题F：特别数的和

小明对数位中含有 2、0、1、9的数字很感兴趣（不包括前导 0），在1到
40中这样的数包括1、2、9、10至32、39和40，共28个，他们的和是574。
请问，在1到n中，所有这样的数的和是多少？
【输入格式】
输入一行包含两个整数n。
【输出格式】
输出一行，包含一个整数，表示满足条件的数的和。
【样例输入】
40
【样例输出】
574
【评测用例规模与约定】
对于20%的评测用例，1≤n≤10。
对于50%的评测用例，1≤n≤100。
对于80%的评测用例，1≤n≤1000。
对于所有评测用例，1≤n≤10000。

def solve(n):
    sum = 0
    for i in range(1, n+1):
        a = str(i)
        if a.count('0') != 0 or a.count('1') != 0 or a.count('2') != 0 or a.count('9') != 0:
            sum += i
    return sum

试题G： 完全二叉树的权值

二叉树基础。。。

import math
n = int(input())
li = list(map(int, input().split()))
height = math.ceil(math.log(n, 2))

res = []
for i in range(1, height+1):
    if i != height:
       res.append(sum(li[2**(i-1)-1:2**i-1]))
    else:
        res.append(sum(li[2**(i-1)-1:]))
print(res.index(max(res))+1)

试题H

数学老师给小明出了一道等差数列求和的题目。但是粗心的小明忘记了一
部分的数列，只记得其中N个整数。
现在给出这 N个整数，小明想知道包含这 N个整数的最短的等差数列有
几项？
【输入格式】
输入的第一行包含一个整数N。
第二行包含 N个整数 A1,A2,···,AN。(注意 A1 ∼AN并不一定是按等差数
列中的顺序给出)
【输出格式】
输出一个整数表示答案。
【样例输入】
5
2641020
【样例输出】
10
【样例说明】
包含2、6、4、10、20的最短的等差数列是2、4、6、8、10、12、14、16、
18、20。
【评测用例规模与约定】
对于所有评测用例，2≤N≤100000

思路：先排序，然后找出最小公差，最后（最大值-最小值）// 公差 + 1

n = int(input())
li = list(map(int, input().split()))
li.sort()
minx = li[1] - li[0]
for i in range(n-1):
    minx = min(minx, li[i+1]-li[i])
ans = (li[-1]-li[0])//minx + 1
print(ans)

试题I： 后缀表达式

给定 N个加号、M个减号以及 N+M+1个整数 A1,A2,···,AN+M+1，小
明想知道在所有由这N个加号、M个减号以及N+M+1个整数凑出的合法的
后缀表达式中，结果最大的是哪一个？
请你输出这个最大的结果。
例如使用123±，则“23+1-”这个后缀表达式结果是4，是最大的。
【输入格式】
第一行包含两个整数N和 M。
第二行包含N+M+1个整数A1,A2,···,AN+M+1。
【输出格式】
输出一个整数，代表答案。
【样例输入】
11
123
【样例输出】
4
【评测用例规模与约定】
对于所有评测用例，0≤N,M≤100000，−10e9 ≤Ai≤10e9。

import itertools
l = list(map(int, input().split()))
li = list(map(int, input().split()))
total = sum(li)
n = l[0]
m = l[1]
he = list(itertools.combinations(li, n+1))
res = 2*sum(li[:n+1])-total
for i in he:
    res = max(res, sum(i)-(total-sum(i)))
print(res)

试题J：灵能传输

额。。。我放弃了