六自由度机械臂建模仿真(matlab程序),有控制面板,代码可流畅运行 1、机器人运动学正逆解、动力学建模仿真与轨迹规划,雅克比矩阵求解 2、蒙特卡洛采样画出末端执行器工作空间 3、基于时间最
六自由度机械臂建模仿真:从理论到Matlab实践
在机器人领域,六自由度机械臂因其高度的灵活性和广泛的应用场景,一直是研究的热门对象。今天咱就聊聊如何通过Matlab来实现六自由度机械臂的建模仿真,还带着个控制面板,代码跑起来溜溜的。
一、机器人运动学正逆解、动力学建模仿真与轨迹规划,雅克比矩阵求解
运动学正解
运动学正解就是已知机械臂各个关节的角度,求末端执行器的位置和姿态。在Matlab里,咱们可以借助Robotics System Toolbox来简化这个过程。假设我们已经定义好了机械臂的DH参数(Denavit - Hartenberg参数),代码示例如下:
% 定义DH参数
L1 = Link('d', 0.1, 'a', 0, 'alpha', pi/2);
L2 = Link('d', 0, 'a', 0.2, 'alpha', 0);
L3 = Link('d', 0, 'a', 0.2, 'alpha', 0);
L4 = Link('d', 0.3, 'a', 0, 'alpha', pi/2);
L5 = Link('d', 0, 'a', 0, 'alpha', -pi/2);
L6 = Link('d', 0.1, 'a', 0, 'alpha', 0);
robot = SerialLink([L1 L2 L3 L4 L5 L6], 'name', 'MyRobot');
% 设定关节角度
q = [pi/4, pi/6, pi/8, pi/10, pi/12, pi/14];
% 求解运动学正解
T = robot.fkine(q);
这里,通过Link函数定义每个关节的DH参数,再用SerialLink组合成完整的机械臂模型。fkine函数就是用来求解运动学正解的,输入关节角度q,就能得到末端执行器的齐次变换矩阵T。
运动学逆解
运动学逆解和正解相反,是已知末端执行器的位置和姿态,求各个关节的角度。Matlab里直接用ikine函数就能搞定:
% 假设已知目标位置和姿态
T_target = transl(0.5, 0.3, 0.4) * trotz(pi/3) * troty(pi/4) * trotx(pi/5);
% 求解运动学逆解
q_sol = robot.ikine(T_target);
transl和trotx、troty、trotz等函数用来构建目标的齐次变换矩阵T_target,ikine函数求解出满足该目标的关节角度q_sol。
动力学建模仿真
动力学建模主要是研究机械臂运动时的力和力矩关系。在Matlab里,我们可以利用robot.dyn函数来获取机械臂的动力学参数。
% 获取动力学参数
M = robot.dyn(q, 'M'); % 惯性矩阵
C = robot.dyn(q, 'C'); % 科里奥利力和离心力矩阵
G = robot.dyn(q, 'G'); % 重力向量
通过这些参数,我们就能进一步做动力学仿真,比如模拟在特定外力作用下机械臂的运动。
轨迹规划
轨迹规划就是让机械臂按照我们期望的路径运动。常见的有笛卡尔空间轨迹规划和关节空间轨迹规划。下面是一个简单的关节空间轨迹规划示例:
% 起始和目标关节角度
q_start = [0, 0, 0, 0, 0, 0];
q_end = [pi/2, pi/3, pi/4, pi/5, pi/6, pi/7];
% 规划轨迹
t = 0:0.01:5; % 时间向量
q_path = jtraj(q_start, q_end, t);
jtraj函数根据起始和目标关节角度,在给定的时间向量t内规划出一条平滑的关节空间轨迹q_path。
雅克比矩阵求解
雅克比矩阵描述了关节速度和末端执行器速度之间的关系。在Matlab里用jacob0函数就能得到:
J = robot.jacob0(q);
这个J矩阵对于很多控制算法都非常重要,比如在速度控制中,我们可以通过它来计算需要给各个关节施加的速度。
二、蒙特卡洛采样画出末端执行器工作空间
蒙特卡洛采样是一种通过随机采样来估计工作空间的方法。代码如下:
num_samples = 10000;
workspace = zeros(num_samples, 3);
for i = 1:num_samples
% 随机生成关节角度
q_random = 2 * pi * rand(6, 1);
T = robot.fkine(q_random);
workspace(i, :) = T(1:3, 4);
end
scatter3(workspace(:, 1), workspace(:, 2), workspace(:, 3));
xlabel('X');
ylabel('Y');
zlabel('Z');
title('End - Effector Workspace');
这里我们随机生成num_samples组关节角度,通过运动学正解得到对应的末端执行器位置,然后用scatter3函数将这些位置点画出来,就能直观看到末端执行器的工作空间啦。
三、基于时间最优的改进粒子群优化算法机械臂轨迹规划设计
粒子群优化算法(PSO)是一种智能优化算法。改进的PSO算法可以用来寻找时间最优的轨迹。下面是一个简化的实现思路:
% 初始化粒子群
num_particles = 50;
num_dimensions = length(q_path);
particles = rand(num_particles, num_dimensions);
velocities = zeros(num_particles, num_dimensions);
% 定义适应度函数(这里简化为时间相关的函数)
fitness = @(x) sum(diff(x).^2);
% 迭代更新粒子位置和速度
for iter = 1:100
for i = 1:num_particles
fitness_values(i) = fitness(particles(i, :));
if fitness_values(i) < fitness(pbest_fitness(i))
pbest(i, :) = particles(i, :);
pbest_fitness(i) = fitness_values(i);
end
end
[global_best_fitness, global_best_index] = min(pbest_fitness);
global_best = pbest(global_best_index, :);
% 更新速度和位置
w = 0.7; % 惯性权重
c1 = 1.5; % 学习因子1
c2 = 1.5; % 学习因子2
r1 = rand(num_particles, num_dimensions);
r2 = rand(num_particles, num_dimensions);
velocities = w * velocities + c1 * r1.* (pbest - particles) + c2 * r2.* (repmat(global_best, num_particles, 1) - particles);
particles = particles + velocities;
end
这里我们初始化了粒子群,定义了一个简单的适应度函数(和运动时间相关),然后通过不断迭代更新粒子的位置和速度,最终找到一个近似的时间最优轨迹。
有了这些内容,再搭配上一个控制面板,就能更方便地对六自由度机械臂进行各种操作和观察啦。无论是调整参数,还是切换不同的仿真模式,都能让整个建模仿真过程更加直观和有趣。希望大家也能通过Matlab深入探索六自由度机械臂的奇妙世界。
六自由度机械臂的建模仿真就像在虚拟世界里造一台钢铁手臂。咱们先撸起袖子从基础开始——正运动学建模。用Matlab的Robotics Toolbox创建机械臂模型简直不要太方便:
% 定义DH参数(标准型)
L(1) = Link('d', 0.3, 'a', 0, 'alpha', pi/2);
L(2) = Link('d', 0, 'a', 0.5, 'alpha', 0);
L(3) = Link('d', 0, 'a', 0.3, 'alpha', 0);
L(4) = Link('d', 0.4, 'a', 0, 'alpha', pi/2);
L(5) = Link('d', 0, 'a', 0, 'alpha', -pi/2);
L(6) = Link('d', 0.1, 'a', 0, 'alpha', 0);
robot = SerialLink(L, 'name', '6DOF');
这段代码定义了一个典型6轴机械臂。Link函数的参数顺序要特别注意:先是关节转角θ,接着是连杆偏移d,连杆长度a,最后是扭转角α。运行robot.teach()会弹出交互界面,拖动滑块就能实时观察机械臂姿态变化。
逆运动学才是真功夫。比如让末端到达某个目标位姿:
T = transl(0.5, 0.2, 0.3)*troty(pi/3); % 目标位姿
q = robot.ikine(T, 'mask', [1 1 1 0 0 0]); % 数值解法
disp('逆解结果:');
disp(q);
这里用了ikine函数做数值逆解,mask参数控制位置和姿态的权重。实际操作中会遇到多解问题,这时候就需要根据关节限制或者能量最优来选择合适解。
工作空间可视化用蒙特卡洛采样最直观:
N = 5000; % 采样点数量
workspace = zeros(N,3);
for i = 1:N
q_rand = rand(1,6)*2*pi - pi; % 随机关节角
T = robot.fkine(q_rand);
workspace(i,:) = T.t(1:3)';
end
scatter3(workspace(:,1), workspace(:,2), workspace(:,3), 5, 'filled');
跑完这段代码,你会看到末端执行器能到达的区域像一朵三维的云团。采样次数越多形状越精确,但别设太大当心卡死电脑。
轨迹规划中的粒子群算法改进版很有意思。核心代码结构大概长这样:
function [best_time, best_path] = PSO_optimize()
% 参数初始化
particle_num = 30;
max_iter = 100;
c1 = 1.5; c2 = 1.7; % 加速因子
w = 0.6; % 惯性权重
% 粒子初始化
particles = struct('position',[],'velocity',[],'cost',inf);
for i=1:particle_num
particles(i).position = rand(1,5)*total_time; % 时间节点
particles(i).velocity = zeros(1,5);
end
% 主循环
for iter=1:max_iter
for i=1:particle_num
% 计算轨迹时间成本
current_cost = fitness(particles(i).position);
% 更新个体最优
if current_cost < particles(i).cost
particles(i).cost = current_cost;
particles(i).best_pos = particles(i).position;
end
% 更新全局最优
if current_cost < global_best.cost
global_best = particles(i);
end
% 速度更新公式
particles(i).velocity = w*particles(i).velocity + ...
c1*rand().*(particles(i).best_pos - particles(i).position) + ...
c2*rand().*(global_best.position - particles(i).position);
% 位置更新
particles(i).position = particles(i).position + particles(i).velocity;
end
end
end
这个改进版在传统粒子群基础上增加了自适应权重调整,fitness函数里通常会混合时间代价和运动平滑性指标。实际调试时发现,加速度约束的处理方式直接影响优化效果,需要给关节力矩留出余量。
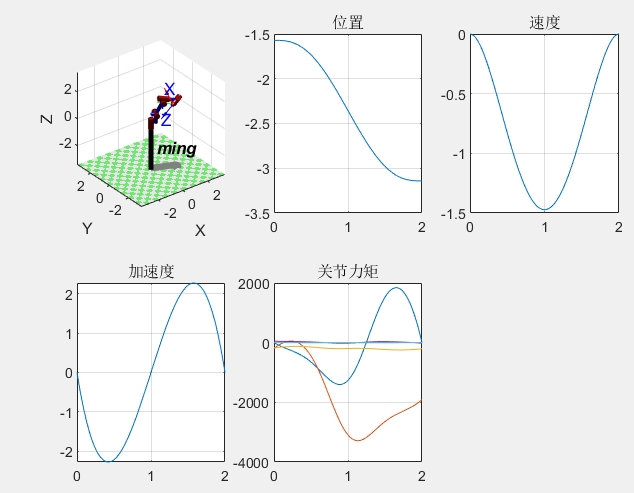
代码跑起来后,控制面板的GUI设计也不能马虎。用Matlab的App Designer拖拽出按钮和坐标系显示区域,回调函数里绑定正逆解计算和动画演示。特别是轨迹规划模块,要实时显示关节角度变化曲线和三维轨迹,这对排查奇异点问题帮助很大。
建完模型别急着跑,先检查雅可比矩阵是否正常:
J = robot.jacob0(q_current);
cond(J) % 条件数过大说明接近奇异位形
动力学仿真部分,推荐用fdyn函数做正向动力学积分。调试时发现,计算力矩控制需要精细调节PD参数,刚开始容易超调,这时候加点速度前馈会稳很多。
最后说点踩坑经验:DH参数千万不能搞反顺序,曾经因为把a和d参数写反,调试了一整天运动轨迹都不对;蒙特卡洛采样的边界条件要设置合理,特别是关节限位没处理好会导致工作空间出现异常凸起;粒子群算法容易陷入局部最优,可以试试加入模拟退火机制或者遗传算法的交叉操作。
六自由度机械臂建模仿真(matlab程序),有控制面板,代码可流畅运行
1、机器人运动学正逆解、动力学建模仿真与轨迹规划,雅克比矩阵求解
2、蒙特卡洛采样画出末端执行器工作空间
3、基于时间最优的改进粒子群优化算法机械臂轨迹规划设计




























 53
53

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








