本文详细介绍了四种经典的排序算法：冒泡排序、归并排序、快速排序和堆排序。冒泡排序通过相邻元素比较交换实现排序，时间复杂度为O(N^2)。归并排序采用分治策略，时间复杂度为O(NlogN)，但需要额外空间。快速排序在平均情况下时间复杂度也为O(NlogN)，但最坏情况达到O(N^2)。堆排序利用堆的性质，时间复杂度同样为O(NlogN)，但稳定性较差。四种排序算法各有优缺点，适用于不同场景。
冒泡排序
思路
- 从头到尾比较相邻两个元素的大小，如果前面的元素比后面的元素大就交换他们的位置（从小到大排序）。这样第一次就会把最大的数排在最后，需要n-1次交换。
- 然后重复上面的做法，因为第一次已经得到最大的数，所以第二次只需要n-2次交换操作，以此类推。
代码
//按照刚才那个动图进行对应
//冒泡排序两两比较的元素是没有被排序过的元素--->
public void bubbleSort(int[] array){
for(int i=0;i<array.length-1;i++){//控制比较轮次，一共 n-1 趟
for(int j=0;j<array.length-1-i;j++){//控制两个挨着的元素进行比较
if(array[j] > array[j+1]){
int temp = array[j];
array[j] = array[j+1];
array[j+1] = temp;
}
}
}
}
算法复杂度
O = N^2
计算过程：
该排序的不足
有重复操作，如有一个数组 3，2，1，在该排序的过程中我们会依次比较3>2,3>1,2>1,但实际上当3>2,2>1时，我们就可以知道3>1了.
归并排序
思路
- 设有一个待排序的数组，他的长度是n，我们需要对其从小到大排序。首先我们把它分成2份a1、a2，每份元素个数为n/2，
- 假设a1，a2他们都已经排好序了，这时我们只需要先比较他们的第一个元素哪个小，然后把小的元素排在第一个。如a1的第一个元素a1-1比较小，我们接着就拿a2的第一个元素继续与a1的第二元素比较，谁小谁放在a1-1后面，以此类推。
- 接下来再思考如何得到上述的a1，a2.同样的方法我们把a1和a2分成2份，然后像这样递归。一直递归到只剩一个元素。然后按照2中的方法进行比较。
代码
public class MergeSort{
//归并排序(升序，调用时left传数组第一个元数的标号，right传最后一个元素的标号)
public static void mergeSort(int[] sorted,int left,int right){
int min = (left + right) / 2;
if(left < right){
//将序列分为左右两个子序列
//再分别对左右两个子序列再分为左右两个子序列
mergerSort(sorted,left,min);
mergerSort(sorted,min + 1,right);
//排序并合并
int[] temp = new int[right - left + 1]
int i = left;
int j = min + 1;
int k = 0;
while(i <= min && j <= right){
if(sorted[i] < sorted[j]){
temp[k++] = sorted[i++];
}else{
temp[k++] = sorted[j++];
}
}
//将左边剩余的数据放入新数组
while(i <= min){
temp[k++] = sorted[i++];
}
//将右边剩余的数据放入新数组
while(j <= right){
temp[k++] = sorted[j++];
}
//排好序的新数组覆盖原数组
for(int n = 0;n < temp.length;n++){
sorted[n + left] = temp[n];
}
}
}
}
算法复杂度
O = NlogN
计算过程
- 因为二等分，所以一共需要递归logN次
- 每次的排序时需要计算N次
- 因此算法复杂度 O = NlogN
该排序的不足
- 需要利用一倍的空间存储计算中间结果temp[]
- 采用二法，没有利用数组的本身的特性，大多数数组其实在局部都存在一些已经排好序的情况，其实可以利用一下（如蒂姆排序算法），如4123，如果分成4,123计算效率可以更高
快速排序
思路
- 随机选取数组其中一个数，比如取第一个n1
- 把小于他的数放左边得到数组a1，大于他的数放右边得到a2
这一部的具体做法为：先从最右向左与n1比较，记录第一个小于n1的位置j；然后从最左向最右比找到第一个大于n1的位置i。然后交换i和j位置上的元素。一直到i和j都指向同一个位置，即把数组遍历完成的时候。最后交换n1和i位置上的元素。参考：https://blog.youkuaiyun.com/qq_40941722/article/details/94396010 - 对2中数组的a1,a2重复1中的操作，如此一直递归操作
- 当数组都只有1个数时，结束递归，按照“左边-中枢-右边”的次序合并，就得到了从小到大排序好的数组。
总体流程：
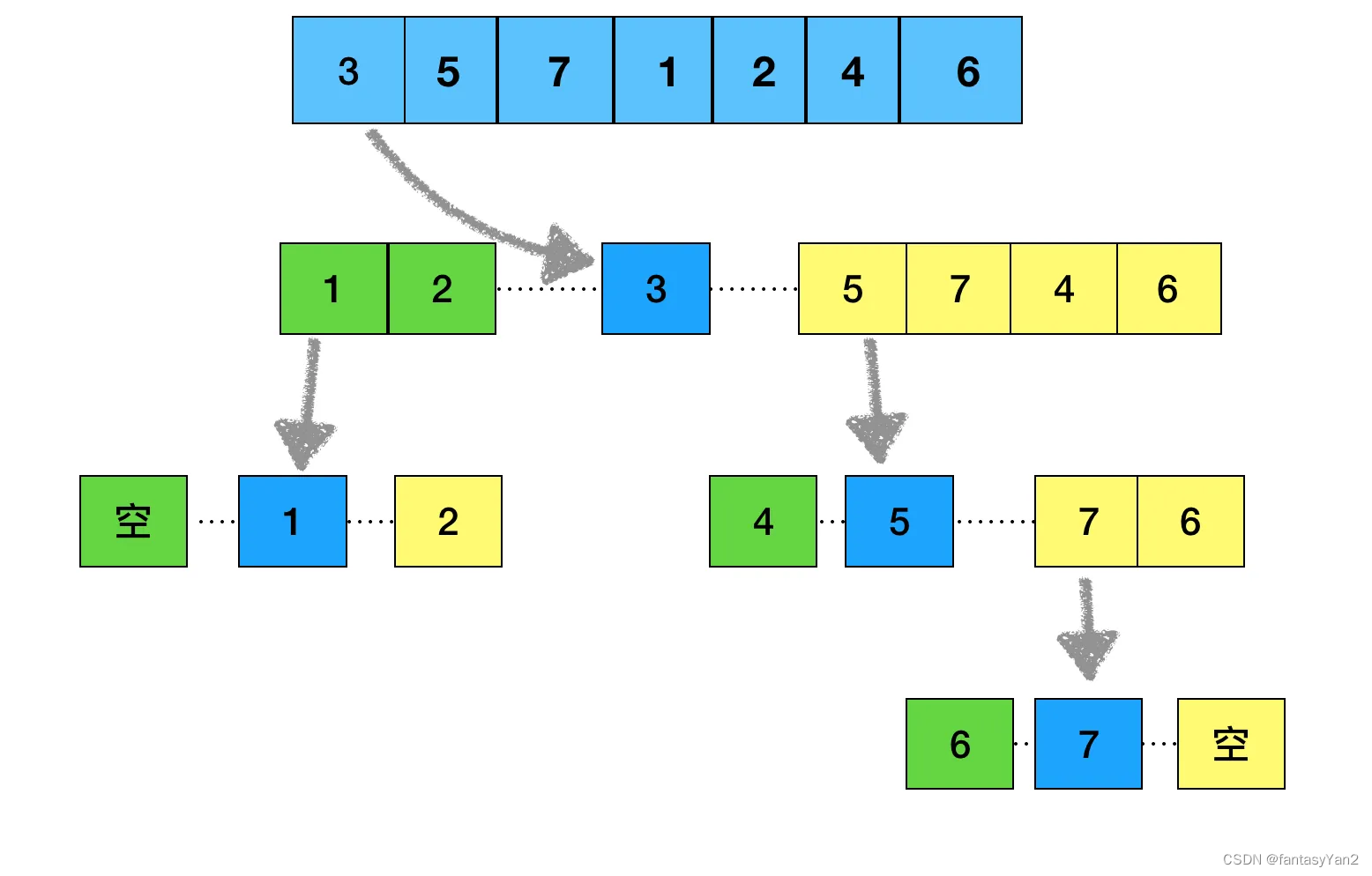
代码
/**
* 快速排序（从小到大）
* @param arr 待排序数组
* @param left 最外层调用时填0
* @param right 最外层调用时选arr.length-1
*/
public static void quickSort(int arr[], int left, int right){
if(left > right){
return;
}
//基准值(一般为首个）
int tmp = arr[left];
int i = left;
int j = right;
//当i与j 相遇时，循环结束
while(i != j){
//先从右边向左走，如果遇到小于基准值的数，则j不动
while(arr[j] >= tmp && j > i) {
j--;
}
//i向前走，遇到大于基准值的数，i不动
while(arr[i] <= tmp && j > i) {
i++;
}
if(j > i){ //当i与j都找到相应的数后，i与j指向的数值互换
int t = arr[i];
arr[i] = arr[j];
arr[j] = t;
}
}
/*当i=j时，说明i与j相遇
* 此时将a[i]与一开始定义的基准值交换
* 从而保证了 基准值的右边都比基准值大，左边都比基准值小
* */
arr[left] = arr[i];
arr[i] = tmp;
//对左边进行排序
quickSort(arr, left, i-1);
//对右边进行排序
quickSort(arr, i+1, right);
}
算法复杂度
O = [NlogN，N^2]
计算过程
- 假设每次子序列分的比例为r:1-r
- 那么递归的第一层我们需要比较n次，第二层为nr+n(1-r)次，即也为n次，因此每层都需要计算n次
- 而递归的深度L，为在log1/rn和n-1中取一个小的。如r=1/2时他的深度为logN，当r=1//N时，即次都是分成一个元素和其他元素，他的深度就为n
- 因O=n×L，所以O的范围为nlogn到n^2之间
该排序的不足
- 该排序计算效率不稳定，最坏的情况需要计算n^2次。不过根据经验这种情况很少见，通常因为此种算法不需要开辟而外的存储空间，一般能比归并排序还快3倍左右。 （更多快速排序为什么快的原因参考：http://mindhacks.cn/2008/06/13/why-is-quicksort-so-quick/）
- 该排序对如：班级里有这两名学生a1（小王，16，北京），a2（小王，16，上海） 进行先根据姓名排序，再根据年龄排序时无法保证a1都能排到a2后面*
原因描述需完善*
堆排序
参考：https://blog.youkuaiyun.com/TaylorSwiftiiln/article/details/119865970
堆
- 堆分大顶堆和小顶堆，每个节点的值都大于或者等于其左右子节点的值，称为大顶堆；或者每个节点的值都小于或者等于其左右子节点的值，称为小顶堆。
- 大顶堆用升序排序，小顶堆用于降序
- 堆的逻辑结果为平衡二叉树，实际存储结构为数组
该数组从逻辑上讲就是一个堆结构，并且有以下特点：
大顶堆：arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]
小顶堆：arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]
思路
- 将无序序列建成一个堆，具体做法为：
从最后一个非叶子节点a开始检查，从他的叶子节点中挑选大的节点b与a比较，交换a和b；按照这个方式，从右向左，然后再从下向上完成交换（交换后需要考虑其页子节点是否满足堆结构，不满足也按上述步骤进行交换）。等执行到根节点，就表示对所有的节点完成了遍历。即把无序数组排成了堆。 - 将堆顶元素与末尾元素交换，将最大元素c沉到数组末端。
- 调整数组，使除了c外，其他的元素构成堆，具体做法：
因为此时末尾的元素已经排好序，所以只需要我们对剩下n-1个元素进行1中的操作，使其变为堆。
因为之前除了堆顶元素因为与最大元素c的交换，不满足堆结构，其他节点已满足堆结构，所以我们从堆节点开始重复1的操作，使新的数组满足堆结构。 - 重复以上操作，直到数组的所有元素都像c一样排好序。
代码
/**
* 堆排序
* @param array 待排序数组
*/
public static void heapSort(int[] array) {
//从倒数第一个非叶子节点开始
for (int i = array.length / 2 - 1; i >= 0; i--) {
//从第一天非叶子节点从左至右，从下至上调整结构
adjustHeap(array, i, array.length);
}
//将堆顶元素与末尾元素交换 将最大元素沉到数组末尾 + 重新调整堆结构
for (int i = array.length - 1; i > 0; i--) {
//交换堆顶元素和末尾元素
swap(array, i);
//交换后的末尾元素忽略(j--) 不再参与堆结构的调整
//重新调整堆结构
adjustHeap(array, 0, i);
}
}
/**
* 交换堆顶元素和末尾元素
* @param array
* @param end 末尾元素序号
*/
private static void swap(int[] array, int end) {
int temp = array[0];
array[0] = array[end];
array[end] = temp;
}
/**
* 使当前节点和其子节点满足堆结构
* @param array
* @param index
* @param length
*/
private static void adjustHeap(int[] array, int index, int length) {
//取出当前元素
int temp = array[index];
//i节点是index节点的左子节点
for (int i = 2 * index + 1; i < length; i = 2 * i + 1) {
//表明左子节点小于右子节点
if (i + 1 < length && array[i] < array[i + 1]) {
//将指针移至较大节点
i++;
}
//如果子节点大于父节点
if (array[i] > temp) {
//将较大值赋给当前节点
array[index] = array[i];
//指针移向子节点
index = i;
} else {
break;
}
}
//循环结束，已经将最大值放在了堆顶
//将temp值放到最终的位置
array[index] = temp;
}
算法复杂度
O=NlogN
参考：https://blog.youkuaiyun.com/yizhiniu_xuyw/article/details/109596961
- 由于堆排序是由两部分(初始化建堆 + 排序重建堆)完成的，所以时间复杂度也应该是两部分之和。
- 初始化建堆当每一次比较都是父节点大于子节点时，只在比较上用了时间，也就是初始化建堆的最好算法复杂度为O=n. 当每一次比较父节点都不比子节点大时，就需要在比较的基础上做调整的工作，一直调整到倒数第二层，他的公式为：
3.对于排序重建堆，一共需要重建n-1次，每一次需要重建的次数-1，且需要比较的次数为log（剩余元素个数），因此他的复杂度为；
：log2+log3+…+log(n-1)+log(n)≈log(n!)。可以证明log(n!)和nlog(n)是同阶函数：
∵(n/2)n/2≤n!≤nn,∵(n/2)n/2≤n!≤nn,
∴n/4log(n)=n/2log(n1/2)≤n/2log(n/2)≤log(n!)≤nlog(n)∴n/4log(n)=n/2log(n1/2)≤n/2log(n/2)≤log(n!)≤nlog(n)
所以时间复杂度为O(nlogn)
4. 所以堆排序的时间复杂度为nlogn
该排序不足
1.局部性差，堆排序的建堆过程是整个数组各个位置都访问到的，后面则是所有未排序数据各个位置都可能访问到的，所以不利于缓存发挥作用。
2. 主要就是两大类：1.基于划分（partition）的，先划分再递归；2.基于归并（merge）的，先递归再归并。基于划分的算法根据划分标准的不同，包括：快速排序、抽样排序、桶排序、自顶向下的基数排序，等等。其中递归部分可以简单地并行。为了不跑题就不讲划分过程和归并过程怎么并行了，这两个部分的并行效率虽然不高，但是也比堆排序好多了。
常见高效排序算法对比
| 算法 | 平均时间复杂度 | 最坏时间复杂度 | 额外空间复杂度 | 稳定性 |
|---|---|---|---|---|
| 归并排序 | NlogN | NlohN | N | 好 |
| 快速排序 | NlogN | NlohN | 1 | 差 |
| 堆排序 | NlogN | N^2 | logN | 差 |
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
