leetcode 974. 和可被 K 整除的子数组（优质解法）

代码：
 

class Solution {
    public int subarraysDivByK(int[] nums, int k) {
        HashMap<Integer,Integer> hashMap=new HashMap();
        hashMap.put(0,1);

        int count=0;    //记录子数组的个数
        int last=0; //前一个下标的前缀和
        int now=0;  //当前下标的前缀和

        for(int i=0;i<nums.length;i++){
            now=last+nums[i];
            int r=(now%k+k)%k;
            count+=hashMap.getOrDefault(r,0);
            hashMap.put(r,hashMap.getOrDefault(r,0)+1);
            last=now;
        }
        return count;
    }
}

题解：

        涉及到子数组的问题，我们一般采用滑动窗口或者前缀和来解决，滑动窗口适合解决数组中只有正数的题，而前缀和适合解决关于子数组之和的题，本题要判断哪些子数组的和能够被 k 整除，所以适合使用前缀和来解决

        在解题之前，我们要先说明一个定理：同余定理，当（a - b）% c = n (整数) ,就能够推出 a % c = b % c ,这个定理是我们解题的要点，通过下图来说明解题的过程：

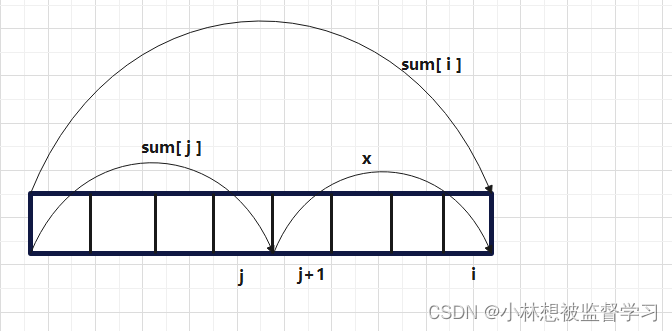
        sum 是前缀和数组，如上图所示，x 是以 i 为尾符合条件的子数组之和，可以推出：sum[ i ] - sum[ j ] = x ,以及 x % k = 0 ，得到 （sum[ i ] - sum[ j ]）% k = 0 ；根据同余定理，推得：sum[ i ] % k = sum[ j ] % k 

        j 是位于 0 ~ i -1 区间中的下标，也就是说在 0 ~ i -1 区间中，找到多少个符合上述条件的前缀和，就知道以 i 下标为尾，符合条件的子数组有多少

        所以我们的思路就是用一个哈希表记录在 i 下标之前所有下标的前缀和 % k 的值对应的个数，以 sum[ i ] % k 为 key，个数为 value，从 0 下标开始遍历数组，在遍历到 i 下标时，我们已经知道了 i -1 下标的前缀和，i 下标的前缀和 sum[ i ] = sum[ i -1 ] +nums[ i ] ,通过 sum[ i ] % k 得到要在哈希表中寻找的 sum[ j ] % k 的值，在哈希表中  sum[ i ] % k 对应的值有多少个，就代表以 i 下标为尾，符合条件的子数组有多少个。

        以该方法遍历所有的下标，便能得到所有符合条件的子数组的个数。

        要注意一个细节，因为数组中存在负数，所以 sum[ i ] 可能为负数，在 java 中，负数 % 正数得到的是负数，为了去除负数的影响，所以在取模时不能直接用  sum[ i ] % k ，而是应该用式子 （ sum[ i ] % k + k）% k

        还有一个细节，当哈希表初始化的时候要直接加上 key = 0，value = 1 的数据，因为不加上的话，就无法记录 nums[ i ] % k = 0 （符合条件的子数组只有 nums[ i ] 这一个数据）这种情况了