笔记——Batch Normalization论文

批量归一化，防止RELU等激活函数的饱和区导致死神经元问题，提高训练效率

To：

饱和非线性的模型（RELU)的输入层的分布会被上游梯度改变，即内部协核漂移（internal covariate shift）（比如说分布变得偏离0位置，大部分甚至全部处于饱和区）为避免这一问题，传统方法会仔细降低学习率或者使用一个很挑剔的初始化参数的方法——批量归一化则能有效地规避这一问题，同时
可以继续使用一个较高的学习率和“随便”初始化；
可以减少对dropout的需求：
可以“放肆”地使用饱和非线性模型

在此之前对BN的探索

1.标准化操作在梯度下降之外的地方计算——对激活之后的输出进行标准化：
现在考虑对权值w和截距b来更新权值的操作，BN在其输出之后发挥作用：
前向传播的过程为：$z=wx+b$，对其进行的归一化操作为：$\hat{z}=z-E[x]$,其中$E[x]$只依赖于输出的各个x，b的改变对其没有影响。在训练过程中，对b的更新为：$b\leftarrow b+△b$其中$▽b\propto \frac{\partial l}{\partial \hat{x}}$,那么$wx+(b+△b)-E(wx+(b+△b))=wx+b-E[wx+b]$,也就是无论截距b如何变化，该项的输出没有任何变化，以至于损失没有任何改变，但是截距却在每次的训练迭代中$b\leftarrow b+△b$不断地累加以至于暴增
2.对每一层的输入的全部样本的全部通道（每个维度的特征层）都执行严苛的标准化（白化），这样的计算代价很大，而且在反向训练时不一定可微

How

通过Mini-Batch统计进行标准化：
1.对于d维度的输入$x=(x^1...x^d)$，对每一个维度实行单独的标准化

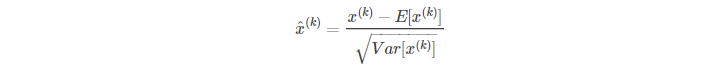
但这种独立标准化每一个维度的特征层的输出，很有可能会改变整个特征层的输出表达，为此加入：

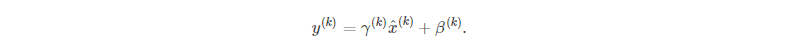
这两个参数也参与网络的训练，一定程度上能恢复网络的表达能力，当：

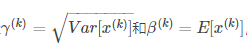
时，就能恢复到标准化之前。
2.在随机优化的过程中，因为训练时，只随机训练并优化一个mini-batch，所以并不对整个输入的数据集求均值并求方差，而是仅仅针对参与训练的当前的数据集进行归一化操作。
前向：

反向：

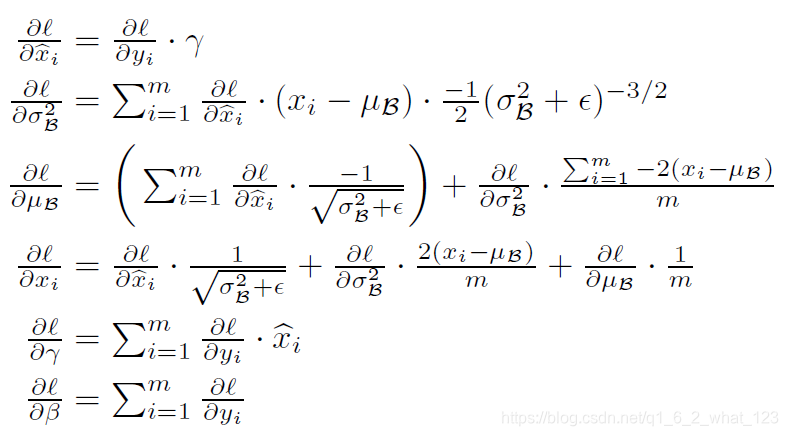
3.卷积网络的BN
$z=g(Wu+b)$中的b可以被$\beta$

实现细节：

1.train

（1）moving average与population average

在训练时，存在 “推断”inference 过程：
计算当前迭代的当前维度的均值和方差，
根据已经存储的前几次迭代的当前维度的均值和方差，
分别计算参与实际运算的均值和方差：
均值：

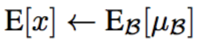
方差的无差估计：

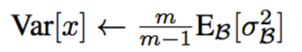
然后分别均值和方差的均值

caffe实现细节
$B{N}_{out}=\lambda B{N}_{new}+(1-\lambda )B{N}_{old}$
$B{N}_{old}=B{N}_{out}$

(2）卷积的BN

如果当前层的输出的feature map的size为pq，则同一维度的m个训练样本的BN操作，一次性参与的数量点的个数为mq*p
截距：原始的卷积加激活的操作表达如下：

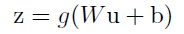
由于截距b作用会被后面的中心化取消（偏置的作用会由前面算法的β来代替），所以，只需要

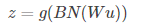
2.test

当网络训练结束时，跑测试集需要的BN，是由训练过程中的所有此的迭代时保存的所有层的所有维度的均值和方差来确定的：
取 对应维度的每次的mean的均值作为测试时该维度的均值
取 对应维度的每次的variance 的无差估计：

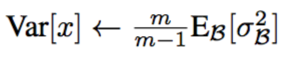
作为当前维度的方差

一系列的Experiments

1.可以提高学习率，可以放大几倍学习率，提前（少量的迭代）达到原本的准确率，却不震荡

2.可以不再使用dropout
3.某程度上更彻底地搅乱了训练样本：与L2正则化类似，内在的随机化将更有效地起到混乱数据集的效果，同时准确率会大一些
4.可以减少L2的约束程度：在BN网络中，可以将正则项的权重缩小了5倍，同时准确率会增大（也就是权值系数的 浮动范围可以更大）
5.删除局部相应归一化
6.减少光照扭曲，直接训练真实的图像数据集就可以