学习算法之旅1——分治法1

#分治法

分治法简单的来说就是将一个问题分为若干个规模较小的子问题，这些子问题的相互独立且与原问题的性质相同，通过求解出子问题的解来解决整个问题，同时遇到复杂的子问题我们可以再将这个子问题再分为若干个子问题，以此类推，直到可以直接求出问题的解为止，这就是分治法的基本思想。

##使用背景
当我们在遇到比较复杂的问题，或者数据量比较的问题，无法直接求解出问题的解， 或者求解过程需要花费大量的精力和时间的时候我们就可以使用分治法来解决问题，通过将问题分为若干个同类型的子问题，求解出子问题的解，找到合适的方法，最后组合求解出整个问题的解。

##解题步骤
分治法的一般求解步骤
1.分解 将问题分为若干个规模较小的同类型的子问题
2.求解 当子问题划分的足够小时，直接求解得到结果
3.合并求解 通过子问题的解逐层合并求解出原问题的解

说到 分治算法自然是会想到二分法，由于二分法的划分的简单和均匀是经常使用的一种方法（后面会详细讲解）

##应用
一、寻找数组中的最大值和最小值
分而治之
将数组分为前后两部分
1.递归求出前一半数组的最大值和最小值
2.递归求出后一半数组的最大值和最小值
3.比较两次求出的的最大值和最小值
得出整个数组的最大值和最小值
这只是一个简单的例子，也算体现出了分治法的思想了，
如果数值长度比较大时可以多分几次。

二分法
假设我们有16个硬币 其中有一个假的（重量比真的偏重一些）
我们有一个天平，找出假的。
利用分治法我们可以将16个硬币分成8组 每组两个硬币，每次比较一个组的硬币重量看是否相等，最多需要8次我们就可以得到假的
二分法 我们将12个硬币分成两组每组6个，比较两组的重量，第一次得到重的一组，再将中的一组分为两组，比较重量，得到重的，继续分成两组比较，依此类推，这样四次就可以得到结果 。
下面我们利用一个数学题来深入了解二分法

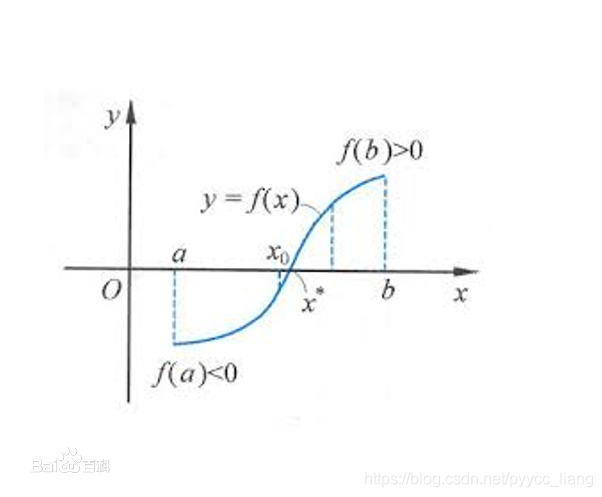
如图求解出f(x)=0的解
由图可知f(a)*f(b)<0
因此我们可以取a,b 的一半的点x0,比较f(x0)*f(a)和f(x0)*f(b),看那个是小于0的，我们再取x0和a或b （乘积小于0的那个点）的一半再比较，依此类推便可求出最优解。资源来源《数值分析》，有兴趣或不懂的可以去深入了解