2019暑假牛客第二场-H-Second Large Rectangle-单调栈（详解）

题面：


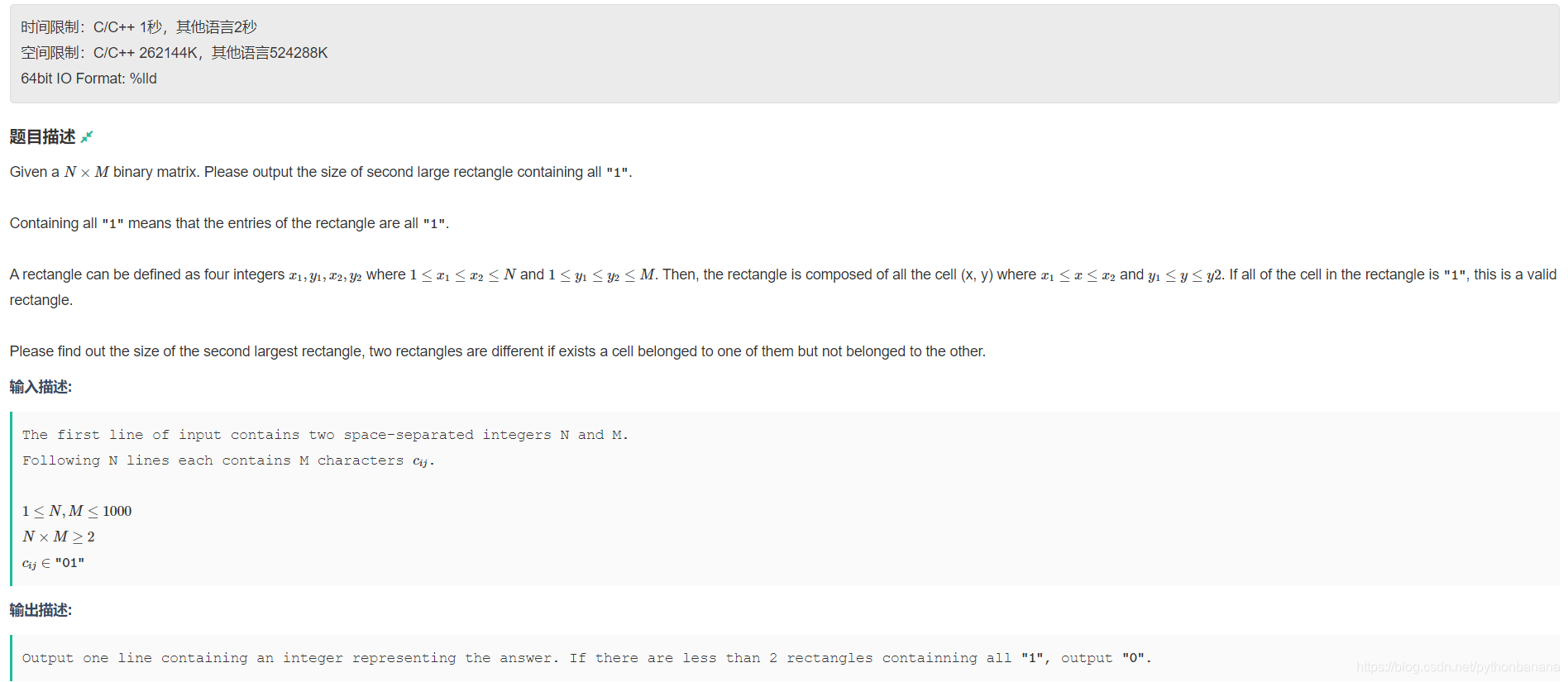
思路：
每一行跑一遍单调栈。
为什么会想到单调栈？
因为在计算矩形的时候，高是由短板决定的（短板效应）。
维护一个单调递增的单调栈。
每个点出栈时，才真正计算有该点的高决定的最大矩形。
每个点在入栈时记录它入栈时弹出的元素，再加上它本身，这记录的是该点向左延伸的最大宽度，但是后面延伸的最大长度，要等到遍历了后面的元素才能知道，所以还要记录一个向后面延伸的最大长度，由后面（高到低）叠加，同时每次记录面积的最大值和次大值。因为每个点计算的是是以该点为右下角的矩形，所以每个点计算出来的矩形都是不一样的矩形，这也为更新最大值，次大值提供了便利。

#include<bits/stdc++.h>
#define per(i,a,b) for(int i = (a);i <= (b);++i)
#define rep(i,a,b) for(int i = (a);i >= (b);--i)
using namespace std;
const int maxn = 1e3 + 10;
int n = 0,m = 0;
char mp[maxn][maxn];
int h[maxn][maxn];
struct node{
	int he,cnt;
};
void init(){
	per(i,0,n){
		per(j,0,m){
			h[i][j] = 0;
		}
	}
}
void solve(){
	init();
	int ans1 = 0,ans2 = 0;
	int len = 0;
	per(i,1,n){
		stack<node> st;
		per(j,1,m){
			if(mp[i][j] == '1'){
				h[i][j] = h[i-1][j] + 1;
			}else{
				h[i][j] = 0;
			}
			len = 0;//记录该点的高度向后可延伸的距离
			//cnt距离该点的高度向前可延伸的距离（他弹出的点的宽度之和）
			while(!st.empty() && st.top().he >= h[i][j]){
				int s1 = st.top().he * (st.top().cnt + len);
				int s2 =  st.top().he * (st.top().cnt + len - 1);

				if(s1 >= ans1){
					ans2 = ans1;
					ans1 = s1;
				}else if(s1 >= ans2){
					ans2 = s1;
				}
				if(s2 >= ans2){//执行s1 >= ans1之后s2 >= ans2仍然可以执行，s1 >= ans0
					ans2 = s2;
				}

				len += st.top().cnt;
				st.pop();
			}
			st.push(node{h[i][j],len + 1});
		}
		len = 0;
		while(!st.empty()){
			int s1 = st.top().he * (st.top().cnt + len);
			int s2 = st.top().he * (st.top().cnt + len - 1);

			if(s1 >= ans1){
				ans2 = ans1;
				ans1 = s1;
			}else if(s1 >= ans2){
				ans2 = s1;
			}
			if(s2 >= ans2){
				ans2 = s2;
			}

			len += st.top().cnt;
			st.pop();
		}
	}
	printf("%d\n",ans2);
}
int main(){
	while(~scanf("%d %d",&n,&m)){
		per(i,1,n){
			scanf("%s",mp[i]+1);
		}
		solve();
	}

	return 0;
}