The 2024 ICPC Asia Hangzhou Regional Contest (2024杭州区域赛AKHEM)

原创已于 2025-10-04 13:29:44 修改 · 1.1k 阅读

9 ·

CC 4.0 BY-SA版权

文章标签：

#ICPC #算法 #数据结构

于 2025-10-04 13:03:31 首次发布

ICPC 区域赛真题详解专栏收录该内容

7 篇文章

订阅专栏

A. AUS

分析：签到，很显然的并查集。

每个字母代表一个节点， $s1$ 和 $s2$ 每个相同位置的对应两个字母代表一条边，在一个连通块中的字母一定是相同的映射值的。

我们想要 $s3$ 和 $s1$ 不相等，就要找到二者相同位置的字母不在同一连通块中（注意只要存在即可直接return）。

时间复杂度： $O(t \cdot (|s_1| + |s_3|))$

#include<bits/stdc++.h>
using namespace std;
#define endl "\n"
#define ll long long

const int N = 27;
int p[N];

int find(int x)
{
    if(x == p[x] )
        return x;
    return p[x] = find(p[x]);
}

void merge(int x ,int y ){
    int rtx = find(x), rty = find(y);
    if(rtx != rty){
        p[rty] = rtx;
    }
}
void init(){
    for (int i = 0; i< N ; i++)
        p[i] = i;
}
void solve(){
    init();
    string s1 , s2 , s3;
    cin >> s1 >> s2 >> s3;
    if(s1.size() != s2.size()){
        cout << "NO" << endl;
        return;
    }
    if(s1.size() == s2.size() && s1.size() != s3.size()){
        cout << "YES" << endl;
        return;
    }

    int n = 26;
    vector<set<int>> adj(n + 1);
    for(int i = 0 ; i < s1.size(); i ++){
        int a = s1[i] - 'a', b = s2[i] - 'a';
        merge(a, b);
    }
    // ab  bc  cd
    for (int i = 0; i < s3.size() ; i ++){
        // 检查是不是存在不在一个集合里面的
        int a = s1[i] - 'a', b = s3[i] - 'a';
        // 如果两者都不在同一个集合里面就输出
        if(find(a) != find(b)){
            cout << "YES" << endl;
            return;
        }
    }
    cout << "NO" << endl;
}

int main(){
	ios_base::sync_with_stdio(false);
	cin.tie(nullptr);
	cout.tie(nullptr);
	int t;
	cin >>t;
	while(t--) solve();
	return 0;
}

分析：观察可以发现如果在某个地方 $x$ 的标记可以达到某行全部被标记，则假设 $x$ 这个地方前面本身已经有 $y$ 个是这一行中的，我们一定不会把它换到 $x$ 右侧，我们只会把不在这一行中的数去和应该在这一行却在 $x$ 右边的数去换，所以我们最多可以换 $k$ 个数，如果 $k >= m$ 则直接全换到前面，标记到m就行了，思路就是这么直接，如果 $k<m$ ，就看哪一行最先达到 $m - k$ 个标记，再加上 $max(k - not_in, 0)$ ，避免 $x$ 实际小于 $m$ 。

时间复杂度： $O(t \cdot n \cdot m)$

#include<bits/stdc++.h>
using namespace std;
#define endl "\n"
#define ll long long
const int N = 100010;
int row[N];  // 记录某一行已经标记了多少个

void solve(){
    int n , m , k ;
    cin >> n >> m >> k ;
    vector<vector<int>> a(n + 1, vector<int>(m + 1));
    for (int i = 0; i < n; i ++)
        row[i] = 0;
    
    for (int i = 0; i < n; i ++){
        for (int j = 0; j < m; j++){
            cin >> a[i][j];
        }
    }
    if (m - k <= 0)
    {
        cout << m << endl;
        return;
    }
    //  还要记录不在的数量
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < m; j++)
        {
            int x = a[i][j];
            int x_row = (x - 1) / m; // 计算出行
            row[x_row]++;
            if (row[x_row] == m - k)
            {
                int sum = i * m + (j + 1);
                int not_in = sum - (m - k); 
                // 这个数量小于k就需要补充一些
                int ans = sum + max(k - not_in, 0);
                cout << ans << endl;
                return;
            }
        }
    }
}

int main(){
	ios_base::sync_with_stdio(false);
	cin.tie(nullptr);
	cout.tie(nullptr);
	int t;
	cin >>t;
	while(t--) solve();
	return 0;
}

H. Heavy-light Decomposition

分析：思维构造。

最长链的起点我们一定是会作为根的，对于次长链，和短链，以及相同的链，有什么比较好的构造方案呢？通过思考可以发现如果 最长链+任意一个可以接在长链上的短链 > 其余的任何链的长度，不管最长链是不是唯一，这时其余的链只需要接在根上即可。

可是我们发现短链必须要 $0 \le \text{len} < \text{mx} - 1$ 才能起加固长链的作用，假如 $len = mx - 1$ 会发现这条链的尝试是最长链 + 1 显然与最长链冲突。

case1：如果存在短链，则最长链+短链一定可以>其余任何链的长度，所以只需要把其余的链都连到根上即可。

case2：如果不存在短链，就代表我们加固不了长链，其余的链还是直接往根上连最优，这个时候发现，不能存在和最长链相同长度的链，否则该链连到根上长度会变成最长链 + 1，显然冲突。

本质上无解的情况就是：存在两个或以上最长链且不存在一个 len < 最长链-1的短链。

时间复杂度： $O(t \cdot (n + k \log k))$

#include<bits/stdc++.h>
using namespace std;
#define endl "\n"
#define ll long long
#define PII pair<int , int> 
#define x first
#define y second

// 无解的情况：：存在两个或以上最长链且不存在一个 len < 最长链-1的短链
// 其余所有的情况 都可以将满足 len < 最长链-1的短链的短链连到最长链的第二个点的上
// 保证了最长链+短链 > 其他所有链  其余所有链直接连接最长链的起点上即可】

void solve(){
	int n, k; 	
	cin >> n >> k;
	vector<int> fa(n + 1 , 0);  
	priority_queue<PII> q;  // 也可以数组直接排序，反正思路清楚一定不会超时的
	int mn = 1e9;
	for(int i = 0 ; i < k ; i ++){
		int l, r;
		cin >> l >> r;
		int len = r - l;
		q.push({len, l});
		mn = min(mn, len);
		for(int i = l + 1 ; i <= r ; i ++){
			fa[i] = i - 1;
		}
	}
	if(k == 1){
		for (int i = 1; i <= n; i ++ ){
			cout << fa[i] << (i == n ? endl : " ");
		}
		return;
	}
	int mx = q.top().x;   			// 最长链的长度
	if(mn >= 0 && mn < mx - 1 ){    // 存在短链则一定有解
		auto l_mx = q.top().y;
		q.pop();
		while(q.size()){
			auto [len, l] = q.top();
			q.pop();
			if(len == mn){  	  // 短链接到长链第二个点上
				fa[l] = l_mx + 1;
				continue;
			}
			fa[l] = l_mx;
		}
		for (int i = 1;i <= n ; i++){
			cout << fa[i] << (i == n ? endl : " ");
		}
		return;
	} 
	int l_mx = q.top().y;
	q.pop(); 					  // 不存在短链则不能存在两个或更多最长链
	if (q.top().x == mx)  
	{
		cout << "IMPOSSIBLE" << endl;
	}
	else
	{
		while(q.size()){
			auto l = q.top().y;
			q.pop();
			fa[l] = l_mx;
		}
		for (int i = 1; i <= n; i++)
		{
			cout << fa[i] << (i == n ? endl : " ");
		}
	}
}

int main(){
	ios_base::sync_with_stdio(false);
	cin.tie(nullptr);
	cout.tie(nullptr);
	int t;
	cin >>t;
	while(t--) solve();
	return 0;
}

E. Elevator II

分析：思维贪心。

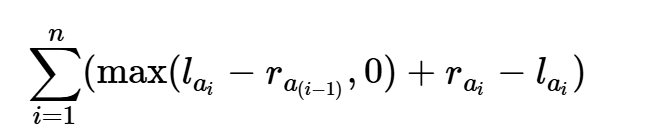
发现sumr - suml一定是一个基础的花费，现在我们想尽可能每次上升都做有用功，减少额外花销，发现如果最开始我们就在最高点，就可以贪心的选r大的进行运人，因为每次的额外花销只和上一次的r有关，上一次的r越大越好， $r >= l_{now}$ 就没有额外花销，所以从最高点开始一定不会产生额外花销。

现在我们唯一的目标就是把走到最上面的这个过程额外花销最小化，需要采取一个贪心的策略。

如果当前的位置是 now ，下一个要送的人是 $[l, r]$ 。

Case1：如果 $l \le \text{now} \le r$ ，则一定不会产生额外花销，还可以让电梯 $now$ 往上走，所以我们先走这样的点。

Case2：如果没有这样的点，我们只能走 $l \ge \text{now} \text{ and } r \ge \text{now}$ 的，本质上额外花销产生的原因就是某段区间没有被上升任务覆盖，为了使额外花销最少，我们要先走 l 最小的产生的额外花销是 $l - now$ 。

这样子走一定可以把覆盖的都走过，其实就是一个简单的区间覆盖问题。

我们保证最小花销到达最高点之后，此后就不会再产生额外花销了，因为我们第二次贪心每次挑 $r$ 大的走，则上一个 $r$ 一定大于当前的 $l$ 。

唯一需要求的就是求从f到最高点之间有多大的区间没有被覆盖，答案就是：

$\text{mn\_cost} = \text{cot\_cover} + \text{sumr} - \text{suml}$

时间复杂度： $O(\sum n \log n)$

#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
#define ll long long
const int N = 100010;
struct node{
    int l, r, id;
} e[N];
void solve()
{
    ll n, f , cost = 0;
    cin >> n >> f;
    vector<int> vis( n + 1 ,  0);
    vector<ll> ans_id;
    for (ll i = 1; i <= n; i++)
    {
        cin >> e[i].l >> e[i].r;
        cost += e[i].r - e[i].l;
        e[i].id = i;
    }
    sort(e + 1, e + 1 + n , [&](node lx, node ly)
    {
        return lx.l < ly.l; 
    });
    ll now = f, not_cover = 0;                  // 寻找f到ed多长的区间没有被覆盖就是not_cover
    int cnt = 0;   
    for (int i = 1; i <= n ; i ++)
    {
        if(e[i].l <= now && e[i].r >= now){   // 这是肯定要选的覆盖的任务
            ans_id.push_back(e[i].id);
            now = e[i].r;
        }else if( e[i].l >= now && e[i].r >= now ){
            not_cover += e[i].l - now;       // 这个时候会产生额外花销，因为没有覆盖
            ans_id.push_back(e[i].id);
            now = e[i].r;
        }else{
            e[++cnt] = e[i]; //存还没有遍历到的
        }
    }
    sort(e + 1, e + 1 + cnt, [&](node lx, node ly)
         { return lx.r > ly.r; });
    // 答案就是cost + not_cover，现在只需要把没有完成的任务按照r排序即可
    for (int i = 1; i <= cnt; i ++){
        ans_id.push_back(e[i].id);
    }
    cout << cost + not_cover << endl;
    for (int i = 1; i <= n; i++){
        cout << ans_id[i - 1] << (i == n ? "\n" : " ");
    }
    return;
}

int main()
{
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    ll t;
    cin >> t;
    while (t--)
        solve();
    return 0;
}

M. Make It Divisible

题意：

给定一个长度为 n 的序列 b 和一个整数 k。你需要找到所有在 1 到 k 范围内的整数 x，使得新序列 a（其中 $a_i = b_i + x$ ）满足一个特殊性质，这个性质被称为“可除序列”。

一个序列是“可除序列”，指的是它的每一个子区间都满足：区间内存在一个“支配者”元素，它可以整除这个区间内的所有其他元素。

分析：数学，笛卡尔树。

不难推断，这个“支配者”必定是该区间内的最小值。

如果直接从 1 到 k 检查每个 x，当 k 很大时一定会超时。所以必须先缩小 x 的范围。

假设mn是数组中最小的数。

根据取模的性质：
，即 。
这个条件必须对所有 $i$ 都成立。因此， $mn+x$ 必须是所有的公约数。
所以， $mn + x$ 必然是的一个因子。代码中的变量 g 就是这个最大公约数。

同样的性质可以推广到任意区间中，可以用相邻两个数的差分 $b_i - b_{i-1}$ 的绝对值来求出公约数（和用最小值 $b_i - mn$ 是一个道理）。

我们就把 $x$ 的搜索范围从可能巨大的，缩小到了 $g$ 的所有因子。对于每个因子，一个候选的就是。

现在我们有了一小组候选的，但还需要验证它们是否真的满足条件。条件是“任意子区间的最小值都能整除该区间所有数”。

我们不可能真的去检查所有 $O(n^2)$ 个子区间。这里用了一个非常聪明的方法：单调栈，这和构建笛卡尔树的思想完全一致。

因为对于笛卡尔树中的任意一个节点，它都是其整个子树（包括它自己）所对应原始区间的最小值。只要一个节点能整除它的所有“直接孩子”，它就必然能整除它的所有“子孙节点”！。

这段代码为序列中的每一个元素，找到了一个最大的连续区间，使得是这个区间内的最小值。
这实际上是在说，在笛卡尔树的结构中，以 $b_i$ 为根节点的子树，对应的就是 $[b_{i,l}, b_{i,r}]$ 这个区间。
现在，我们只需要验证一个简化后的条件：对于每个 $i$ ， $b_i + x$ 是否能整除它所支配的区间 $[b_{i,l}, b_{i,r}]$ 内的所有 。如果这个条件对所有 i 都成立，那么整个序列就是“可除序列”。

auto check = [&](ll add) -> bool
    {
        for (ll i = 1; i <= n; i++)
        {
            ll div = b[i].v + add;
            for (ll j = b[i].l; j <= b[i].r; j++)  // 这一层循环可以优化
            {
                if ((b[j].v + add) % div != 0)
                {
                    return false;
                }
            }
        }
        return true;
    };

这个 check 函数的复杂度是 $O(n^2)$ 的，但因为它只在 $g$ 的因子（数量很少）上被调用，如果不放心的话可以用rmq快速求区间gcd，check的时间复杂度就是 $O(n \log n)$ 。

下列代码中前两个提供另一个思路存单调区间的思路，比较了解笛卡尔树的可以直接看第代码三。

代码一（单调栈不加优化）：

时间复杂度： $O(d(g) \cdot n^2)$

但是竟然没有超时，只能说当数据量很大时有效的因子实在是太少了。

#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define endl "\n"
struct node
{
    ll l, r, v = 0;
};

ll gcd(ll a, ll b)
{
    if (a == 0)
        return b;
    return gcd(b % a, a);
}

void solve()
{
    ll n, k;
    cin >> n >> k;
    vector<node> b(n + 2);
    ll mn = 1e9, mx = 0;
    for (ll i = 1; i <= n; i++)
    {
        cin >> b[i].v;
        mn = min(mn, b[i].v);
        mx = max(mx, b[i].v);
        b[i].l = i, b[i].r = i;
    }
    ll g = 0;
    // 生成所有的 mn
    if (mn == mx)
    {
        cout << k << " " << k * (k + 1) / 2 << endl;
        return;
    }
    for (ll i = 1; i <= n; i++)
    {
        if (b[i].v == mn)
            continue;
        g = gcd(g, b[i].v - mn);
    }
    // 单调栈求出所有的区间
    stack<ll> q;
    q.push(0);
    for (ll i = 1; i <= n; i++)
    {
        while (b[q.top()].v > b[i].v)
            q.pop();
        b[i].l = q.top() + 1;
        q.push(i);
    }
    while (q.size())
        q.pop();
    q.push(n + 1);
    for (ll i = n; i >= 1; i--)
    {
        while (b[q.top()].v > b[i].v)
            q.pop();
        b[i].r = q.top() - 1;
        q.push(i);
    }
    // 初始化每个节点管理的区间
    ll cnt = 0, sum = 0;
    auto check = [&](ll x) -> bool
    {
        for (ll i = 1; i <= n; i++)
        {
            ll div = b[i].v + x;
            for (ll j = b[i].l; j <= b[i].r; j++)
            {
                if ((b[j].v + x) % div != 0)
                {
                    return false;
                }
            }
        }
        return true;
    };
    for (ll i = 1; i * i <= g; i++)
    {
        if (g % i == 0)
        { // 这是一个因数
            ll x = i - mn;
            if (x > 0 && x <= k)
            {
                if (check(x))
                {
                    cnt++;
                    sum += x;
                }
            }
            ll j = g / i;
            x = j - mn;
            if (j != i && x > 0 && x <= k)
            {
                if (check(x))
                {
                    cnt++;
                    sum += x;
                }
            }
        }
    }
    cout << cnt << " " << sum << endl;
}

int main()
{
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    ll t;
    cin >> t;
    while (t--)
        solve();
}

代码二（单调栈RMQ优化）：

理论时间复杂度： $O(n \log n + d(g) \cdot n)$ 。

但和上面的代码速度接近~

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl "\n"
struct elem{
    ll l, r, v = 0 ;
};
const int N = 200010, M = 18;
int n, m;
int w[N], f[N][M];

void solve(){
    ll n, k;
    cin >> n >> k;
    vector<elem> b(n + 2);
    ll mn = 1e9 , mx = 0;
    for (ll i = 1; i <= n; i++)
    {
        cin >> b[i].v;
        mn = min(mn, b[i].v);
        mx = max(mx, b[i].v);
        b[i].l = i, b[i].r = i;
    }
    ll g = 0;
    if(mn == mx){ //直接退出
        cout << k << " " << k * (k + 1) / 2 << endl;
        return;
    }
    for (ll i = 1; i <= n; i++)
    {
        if (b[i].v == mn)
            continue;
        g = __gcd(g, b[i].v - mn);
    }
    // 单调栈求出所有的区间
    stack<ll> q;
    q.push(0);
    for (ll i = 1; i <= n; i++)
    {
        while (b[q.top()].v > b[i].v)
            q.pop();
        b[i].l = q.top() + 1;
        q.push(i);
    }
    while (q.size())
        q.pop();
    q.push(n + 1);
    for (ll i = n; i >= 1; i--)
    {
        while (b[q.top()].v > b[i].v)
            q.pop();
        b[i].r = q.top() - 1;
        q.push(i);
    }
    // 初始化每个节点管理的区间
    ll cnt = 0, sum = 0;
    auto init = [&]() -> void
    {
        for (int j = 0; j < M; j++)
        {
            for (int i = 1; i + (1 << j) - 1 <= n; i++)
                if (!j)
                    f[i][j] = abs(b[i].v - b[i-1].v);  
    // 不能减去mn 因为我们没有单独去求[b[i].l，b[i].r]这个小区间的mn
                else
                    f[i][j] = __gcd(f[i][j - 1], f[i + (1 << j - 1)][j - 1]);
        }
    };
    init();
    auto ask = [&](int la, int rb)->int{   // RMQ询问区间gcd
        int len = rb - la + 1;
        int j = log(len) / log(2);
        return __gcd(f[la][j], f[rb - (1 << j) + 1][j]);
    };

    auto check = [&](ll add) -> bool
    {
        for (ll i = 1; i <= n; i++)
        {
            ll div = b[i].v + add;
            int la = b[i].l, rb = b[i].r;
            if(la == rb)
                continue;
            if (ask(la + 1, rb) % div != 0)
            {
                return false;
            }
        }
        return true;
    };
    vector<int> d; // 存因数
    for (ll i = 1; i * i <= g; i++)
    {
        if (g % i == 0)
        {
            d.push_back(i);
            if (i * i != g)
                d.push_back(g / i);
        }
    }
    for (auto x : d)
    {
        int add = x - mn;
        if (add > 0 && add <= k)
        {
            if (check(add))
            {
                cnt++;
                sum += add;
            }
        }
    }
    cout << cnt << " " << sum << endl;
}

int main(){
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    ll t;
    cin >> t;
    while(t --)
        solve();
}

代码三（笛卡尔树遍历）：

复杂度近似： $O(n \log n + d(g) \cdot n)$ ，效率和上面代码类似。

本质上树遍历的思路是比较直接的。

笛卡尔树建树代码（详细注释）：

int ls[N], rs[N], stk[N];

void build() {
    // top 是栈顶指针，指向 sta 数组中的栈顶位置。0代表栈为空。
    int top = 0;

    // 每次建树前，重置左右孩子数组，防止多组测试数据之间互相影响。
    for (int i = 1; i <= n; i++) ls[i] = rs[i] = 0;

    // 从左到右依次处理每个节点 i
    for (int i = 1; i <= n; i++) {
        // pos 是一个临时指针，从当前栈顶开始，用于寻找节点 i 的插入位置。
        // 这样可以保留原始的栈顶位置 top，方便后续比较。
        int pos = top;

        // --- 核心：单调栈操作 ---
        // 这个循环的目的是找到 i 在“右轮廓”上的正确位置。
        // 只要栈不为空(pos>0)，且栈顶节点的值大于当前节点 b[i] 的值，
        // 就不断将栈顶指针向栈底移动（模拟出栈）。
        // 循环结束后，sta[pos] 将是 i 的父节点。
        while (pos > 0 && b[sta[pos]] > b[i]) {
            pos--;
        }

        // --- 建立连接关系 ---

        // 如果循环结束后栈不为空（pos > 0），
        // 那么新的栈顶 sta[pos] 就是 i 的父节点。
        // 因为 i 的索引比父节点大（即 i 在父节点的右边），所以 i 成为其父节点的右孩子。
        if (pos > 0) {
            rs[sta[pos]] = i;
        }

        // 如果 pos < top，说明刚刚的 while 循环至少弹出了一个元素。
        // sta[pos+1] 就是最后一个被弹出的元素。这个被弹出的子树现在整体作为 i 的左孩子。
        // sta[pos+1] 是这个子树的根，所以它被连接为 i 的左孩子。
        if (pos < top) {
            ls[i] = sta[pos + 1];
        }

        // --- 更新栈 ---
        // 将当前节点 i 的索引压入栈中，放在 pos 指向的位置的下一个。
        sta[++pos] = i;
        // 更新真实的栈顶指针，完成本次操作。
        top = pos;
    }
}

完整代码：

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N = 5e4 + 10; 
int n, k; 
int a[N], b[N];
// 构建笛卡尔树的全局变量
int ls[N], rs[N], sta[N];

void build(){  // 建笛卡尔树
    int top = 0;
    // 初始化，防止旧数据影响
    for(int i = 1; i <= n; i++) ls[i] = rs[i] = 0;
    for(int i = 1; i <= n; i++){
        int pos = top;
        while(pos > 0 && b[sta[pos]] > b[i]){
            pos--;
        }
        if(pos > 0){
            rs[sta[pos]] = i;
        }
        if(pos < top){
            ls[i] = sta[pos+1];
        }
        sta[++pos] = i;
        top = pos;
    }
}

bool dfs(int node, int fa_node){
    // 如果父节点存在，且父节点的值不能整除当前节点的值，则不合法
    if (fa_node != 0 && b[node] % fa_node != 0) {
        return false;
    }
    // 递归检查左子树和右子树
    bool left_ok = true, right_ok = true;
    if (ls[node]) {
        left_ok = dfs(ls[node], b[node]);
    }
    if (rs[node]) {
        right_ok = dfs(rs[node], b[node]);
    }
    return left_ok && right_ok;
}

// check(x)函数: 验证给定的x是否合法
// 这个函数是你的代码的精华，它正确地实现了对一个解的验证
bool check(int add){
    for(int i = 1; i <= n; i++) b[i] = a[i] + add;
    build();
    // 从笛卡尔树的根节点sta[1]开始DFS，根没有父节点，父节点值设为0
    return dfs(sta[1], 0);
}

void solve(){
    cin >> n >> k;
    int mn = 1e9 , mx = 0 ;
    for(int i = 1; i <= n; i++){
        cin >> a[i];
        mn = min(mn, a[i]);
        mx = max(mx, a[i]);
    }
    // 特殊情况：mx == mn
    if(mn == mx){
        cout << k << " " << k * (k + 1) / 2 << "\n";
        return;
    }

    // 步骤1：根据题解思路，生成候选x
    // 计算整个序列相邻元素的差分的GCD
    int g = 0;
    for(int i = 1; i < n; i++){
        g = __gcd(g, abs(a[i + 1] - mn));
    }
    // 找到g的所有因子d
    vector<int>d;
    for(int i = 1; i * i <= g; i++){
        if(g % i == 0){
            d.push_back(i);
            if(i * i != g) d.push_back(g / i);
        }
    }

    int cnt = 0, sum = 0;
    // 步骤2：遍历所有候选x，并用check函数进行验证
    for(int x : d){
        // 根据 (mn + x) = x 反解出候选x
        int add = x - mn;
        // 检查x是否在合法范围内
        if(add < 1 || add > k) continue;
        // 调用验证函数
        if(check(add)) {
            cnt++;
            sum += add;
        }
    }

    cout << cnt << " " << sum << "\n";
}

signed main() {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    int t;
    cin >> t;
    while(t--) solve();
    return 0;
}