题目链接
这道题目可以说是很典的一个题目,解法很多,适合练习,这里给出随机选数、摩尔投票、主席树,三种解法。
题意:给定一个数组,有q次询问,每次询问该数组的一个区间[ l ,r ] ,让你找出其中出现超过 的数,并且输出。
数据范围:
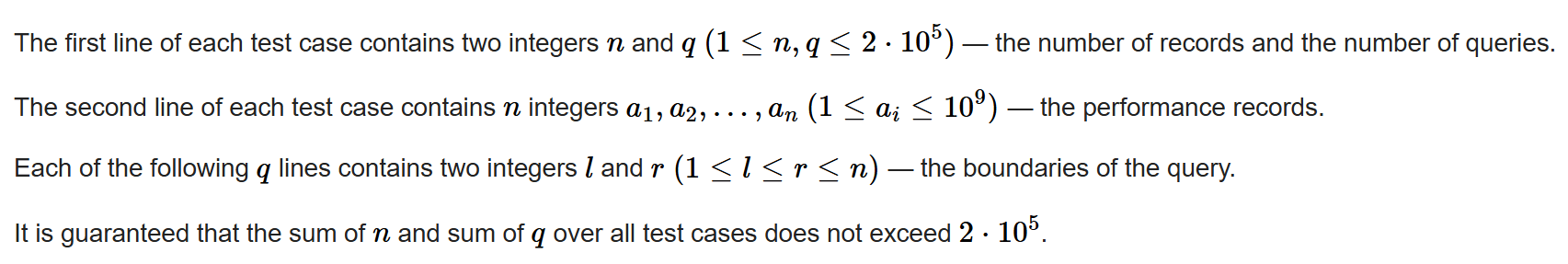
代码一(随机选数)
就是对于一个区间中的数字,每次随机选取一个数字,二分统计这个区间中数字出现的次数,我们随机50次,出错的概率可以小到 。
时间复杂度:
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,q;
int a[200005],b[200005];
vector<int> v[200005];
mt19937 rnd(time(0));
int query(int l,int r,int x)
{
return upper_bound(v[x].begin(),v[x].end(),r)-lower_bound(v[x].begin(),v[x].end(),l);
}
void test()
{
cin>>n>>q;
for(int i=1;i<=n;i++)
cin>>a[i],b[i]=a[i];
sort(b+1,b+n+1);
int m=unique(b+1,b+n+1)-b-1;
for(int i=1;i<=n;i++)
a[i]=lower_bound(b+1,b+m+1,a[i])-b;
for(int i=1;i<=m;i++)
v[i].clear();
for(int i=1;i<=n;i++)
v[a[i]].push_back(i);
for(int i=1;i<=q;i++)
{
int l,r;
cin>>l>>r;
int k=(r-l+1)/3;
set<int> st;
for(int j=1;j<=50;j++)
{
int x=rnd()%(r-l+1)+l;
if(query(l,r,a[x])>k)
st.insert(b[a[x]]);
if(st.size()>=3)
break;
}
for(int x:st)
cout<<x<<" ";
if(st.empty())
cout<<-1;
cout<<"\n";
}
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int t;
cin>>t;
for(int i=1;i<=t;i++)
test();
}代码二(主席树)
主席树一般解决区间第k小问题,在这里其实就是求某区间出现次数大于k的数
重点理解query逻辑就行,目的是找到区间中某一个点的计数 > k ,而不是每次计算一个区间中的数了,但是只有当某个区间中的cnt > k ,我们要找的点才可能存在于这样的区间 ,然后不断收缩,直到找到 ,或者直接路径中断,并用fg标记有没有找到解,没有找到的话就输出-1,找到的话就直接输出,其余就是主席树模板。
核心代码:
void query_k(int u, int v, int l, int r, int k)
{
if (l == r) // 最后收缩到一个点 说明这个点的数量 > k
{
fg = 1;
cout << nums[l - 1] << " ";
return;
}
int diff_l = tr[tr[u].l].cnt - tr[tr[v].l].cnt;
int diff_r = tr[tr[u].r].cnt - tr[tr[v].r].cnt;
int mid = l + r >> 1;
if (k < diff_l) // 右子树找不到再往左子树中找
{
// 第 k 小的数在左子树
query_k(tr[u].l, tr[v].l, l, mid, k);
}
if (k < diff_r)
{
// 第 k 小的数在右子树
query_k(tr[u].r, tr[v].r, mid + 1, r, k);
}
}理解这个直接套模板就行:
时间复杂度:
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 200005; // 序列长度和查询次数的最大值
vector<int> v[N];
int n, m, fg;
int a[N]; // 原始序列
vector<int> nums; // 用于存储所有待离散化的值
// 获取 x 离散化后的排名
int get_id(int x)
{
return lower_bound(nums.begin(), nums.end(), x) - nums.begin() + 1;
}
struct Node
{
int l, r; // 左右子节点的编号
int cnt; // 区间内数的个数
} tr[N * 24]; // 空间大小估算: n * log(n) + m * log(n),开大一些比较保险
int root[N]; // root[i] 存储第 i 个版本的根节点
int tot = 0; // 节点总数
int insert(int p, int l, int r, int x)
{
int q = ++tot; // 创建一个新节点 q
tr[q] = tr[p]; // 复制上一个版本的信息
tr[q].cnt++; // 当前区间的计数值+1
if (l == r)
return q; // 到达叶子节点,返回
int mid = l + r >> 1;
if (x <= mid)
{
// 如果 x 在左半区间,递归更新左子树,并把新左子树的根节点赋给 q->l
tr[q].l = insert(tr[p].l, l, mid, x);
}
else
{
// 否则递归更新右子树
tr[q].r = insert(tr[p].r, mid + 1, r, x);
}
return q; // 返回新节点的编号
}
void query_k(int u, int v, int l, int r, int k)
{
if (l == r) // 最后收缩到一个点 说明这个点的数量 > k
{
fg = 1;
cout << nums[l - 1] << " ";
return;
}
int diff_l = tr[tr[u].l].cnt - tr[tr[v].l].cnt;
int diff_r = tr[tr[u].r].cnt - tr[tr[v].r].cnt;
int mid = l + r >> 1;
if (k < diff_l) // 右子树找不到再往左子树中找
{
// 第 k 小的数在左子树
query_k(tr[u].l, tr[v].l, l, mid, k);
}
if (k < diff_r)
{
// 第 k 小的数在右子树
query_k(tr[u].r, tr[v].r, mid + 1, r, k);
}
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
int t;
cin >> t;
while (t--)
{
tot = 0;
nums.clear();
cin >> n >> m;
for (int i = 1; i <= n; ++i)
{
root[i] = 0;
v[i].clear();
}
for (int i = 1; i <= n; ++i)
{
cin >> a[i];
nums.push_back(a[i]);
}
// 离散化
sort(nums.begin(), nums.end());
nums.erase(unique(nums.begin(), nums.end()), nums.end());
int range = nums.size();
for (int i = 1; i <= n; ++i)
{
int id = get_id(a[i]);
root[i] = insert(root[i - 1], 1, range, id);
}
// 处理 m 次查询
for (int i = 0; i < m; ++i)
{
fg = 0;
int l, r;
set<int> st;
cin >> l >> r;
int k = (r - l + 1) / 3;
query_k(root[r], root[l - 1], 1, range, k);
if (!fg)
cout << -1;
cout << endl;
}
}
return 0;
}
代码三(摩尔投票+线段树)
摩尔投票相比前两者有些麻烦,感兴趣的可以了解一下。
时间复杂度:
#include <iostream>
#include <vector>
#include <algorithm>
#include <map>
using namespace std;
// 线段树节点结构体
struct Node {
pair<int, int> c[2]; // 存储两个候选数 {值id, 票数}
Node() {
c[0] = {0, 0}; // 初始化两个候选数为空
c[1] = {0, 0};
}
};
// 全局变量
vector<int> arr; // 存储原始数组
vector<Node> seg; // 线段树
vector<vector<int>> pos; // 每个值出现的位置列表
map<int, int> val2id; // 值到离散化id的映射
vector<int> id2val; // 离散化id到值的映射
// 合并两个节点的候选信息
Node merge(const Node &l, const Node &r) {
Node res = l; // 以左节点为基础
// 处理右节点的两个候选数
for (int i = 0; i < 2; ++i) {
if (r.c[i].second == 0) continue; // 跳过空候选
int val = r.c[i].first; // 候选数值id
int cnt = r.c[i].second; // 候选数票数
// 情况1: 候选数已在res中
if (res.c[0].first == val) {
res.c[0].second += cnt;
}
// 情况2: 候选数在res的第二个位置
else if (res.c[1].first == val) {
res.c[1].second += cnt;
}
// 情况3: res有空位
else if (res.c[0].second == 0) {
res.c[0] = {val, cnt};
}
else if (res.c[1].second == 0) {
res.c[1] = {val, cnt};
}
// 情况4: 需要三方抵消
else {
// 计算最小票数进行抵消
int minv = min({res.c[0].second, res.c[1].second, cnt});
res.c[0].second -= minv;
res.c[1].second -= minv;
cnt -= minv;
// 抵消后如果还有剩余票数,尝试占据空位
if (cnt > 0) {
if (res.c[0].second == 0) {
res.c[0] = {val, cnt};
} else if (res.c[1].second == 0) {
res.c[1] = {val, cnt};
}
}
}
}
// 清理票数为0的候选
if (res.c[0].second == 0) res.c[0].first = 0;
if (res.c[1].second == 0) res.c[1].first = 0;
// 确保票数多的在前
if (res.c[0].second < res.c[1].second) {
swap(res.c[0], res.c[1]);
}
return res;
}
// 构建线段树
void build(int u, int l, int r) {
if (l == r) { // 叶子节点
seg[u].c[0] = {arr[l], 1}; // 初始候选是自己,票数为1
seg[u].c[1] = {0, 0}; // 第二个候选为空
return;
}
int mid = (l + r) / 2;
build(u * 2, l, mid); // 构建左子树
build(u * 2 + 1, mid + 1, r); // 构建右子树
seg[u] = merge(seg[u * 2], seg[u * 2 + 1]); // 合并子节点信息
}
// 区间查询
Node query(int u, int l, int r, int ql, int qr) {
if (qr < l || r < ql) return Node(); // 查询区间与当前区间无交集
if (ql <= l && r <= qr) return seg[u]; // 当前区间完全包含在查询区间内
int mid = (l + r) / 2;
Node left = query(u * 2, l, mid, ql, qr); // 查询左子树
Node right = query(u * 2 + 1, mid + 1, r, ql, qr); // 查询右子树
return merge(left, right); // 合并左右子树结果
}
// 统计某个值在区间[l,r]内的出现次数
int count_in_range(int id, int l, int r) {
if (id == 0) return 0; // 无效id
auto &p = pos[id]; // 获取该值的所有位置
// 使用二分查找统计在[l,r]范围内的数量
auto itl = lower_bound(p.begin(), p.end(), l);
auto itr = upper_bound(p.begin(), p.end(), r);
return distance(itl, itr);
}
void solve() {
int n, q;
cin >> n >> q;
// 读取并离散化数据
arr.assign(n + 1, 0);
vector<int> tmp(n);
for (int i = 1; i <= n; ++i) {
cin >> arr[i];
tmp[i - 1] = arr[i];
}
// 去重排序
sort(tmp.begin(), tmp.end());
tmp.erase(unique(tmp.begin(), tmp.end()), tmp.end());
// 建立双向映射
val2id.clear();
id2val.assign(tmp.size() + 1, 0);
for (size_t i = 0; i < tmp.size(); ++i) {
val2id[tmp[i]] = i + 1; // 值到id
id2val[i + 1] = tmp[i]; // id到值
}
// 记录每个值的位置
pos.assign(tmp.size() + 1, vector<int>());
for (int i = 1; i <= n; ++i) {
arr[i] = val2id[arr[i]]; // 将值转换为id
pos[arr[i]].push_back(i); // 记录位置
}
// 构建线段树
seg.assign(4 * (n + 1), Node());
build(1, 1, n);
// 处理查询
for (int i = 0; i < q; ++i) {
int l, r;
cin >> l >> r;
Node res = query(1, 1, n, l, r); // 查询区间候选
int len = r - l + 1;
int thr = len / 3; // 阈值
// 验证候选是否满足条件
vector<int> ans;
if (res.c[0].second > 0 && count_in_range(res.c[0].first, l, r) > thr) {
ans.push_back(id2val[res.c[0].first]);
}
if (res.c[1].second > 0 && count_in_range(res.c[1].first, l, r) > thr) {
ans.push_back(id2val[res.c[1].first]);
}
// 去重排序输出
sort(ans.begin(), ans.end());
ans.erase(unique(ans.begin(), ans.end()), ans.end());
if (ans.empty()) {
cout << -1 << "\n";
} else {
for (size_t j = 0; j < ans.size(); ++j) {
cout << ans[j] << (j == ans.size() - 1 ? "" : " ");
}
cout << "\n";
}
}
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
int t;
cin >> t;
while (t--) {
solve();
}
return 0;
}




















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








