统计学基础-周计划1

数据的集中趋势

众数

概念：一组数据中出现次数最多的数，众数可以是多个，也可以没有。
举个栗子：[0,0,1,1,2,3]中的众数是0和1，[0,1,2,3]中没有众数，[0,1,2,1]中的众数是1。

中位数

概念：一组数据中，中间位置的那个数，假设n为奇数，排序之后中间的那个值就是中位数，如果n是偶数，排序之后中间两个数的平均值即为中位数。
举个栗子：假设排序之后的数据为[0,1,2,4,4]，此时的中位数是2，假设排序之后的数据为[0,1,2,3]，此时该组数据的中位数是(1+2)/2=1.5。

分位数

概念：把一组数据分成n等分，则称之为n分位数。常用的有Q1、Q2、Q3，分别为上四分位数，中位数和下四分位数。Q1、Q2、Q3的position分别为Q1_pos=(n+1)*0.25，Q2_pos(n+1)*0.5，Q3_pos=(n+1)*0.75，对应的分位数值见下图的栗子：

极差

概念：一组数据中最大值与最小值之差。
举个栗子：[1,3,5,2,0]的max=5,min=0，so 极差=5-0=5

算数平均数

概念：一组数据之和与个数之比。
举个栗子：[0,1,3,4]的平均数为(0+1+3+4)/4=2

加权平均数

概念：若n个数 的权分别是 ，那么 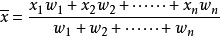叫做这n个数的加权平均值。

几何平均数

概念：对各变量值的连乘积开项数次方根。
举个栗子：一组数据为[1,2,2,4]，则几何平均数为。如果有负数，开根号出来是虚数，如果包含0，就是0了。

数据离散程度

方差

概念：每一个变量（观察值）与总体均数之间的差异，包含样本方差和总体方差。样本方差的分母为n-1，总体方差的分母为n。

标准差

概念：对方差开根号，即可。常用的是样本方差。

平均差

概念：各个变量值同平均数的离差绝对值的算术平均数。

四分位差

概念：上四分位数（Q3，即位于75%）与下四分位数（Q1，即位于25%）的差。

离散系数

概念：当进行两个或多个资料离散程度的比较时，如果度量单位与平均数相同，可以直接利用标准差来比较。如果单位和（或）平均数不同时，比较其离散程度就不能采用标准差，而需采用标准差与平均数的比值（相对值）来比较 ：

异众比率

概念：衡量众数对一组数据的代表程度。异众比率越大，说明非众数组的频数占总频数的比重越大，众数的代表性就越差；异众比率越小，说明非众数组的频数占总频数的比重越小，众数的代表性越好。

偏态系数

概念：数据偏斜程度的测定。

SK表示偏斜系数：偏态系数小于0，因为平均数在众数之左，是一种左偏的分布，又称为负偏。偏态系数大于0，因为均值在众数之右，是一种右偏的分布，又称为正偏；当SK=0时，数据完全对称分布。

峰态系数

概念：数据扁平程度的测定。

当K=3时，扁平程度适中；当K>3时为尖峰分布；当K<3时为扁平分布。