代码随想录算法训练营第七天|LeetCode454.四数相加II、LeetCode383.赎金信、LeetCode15.三数之和、LeetCode18.四数之和-优快云博客

class Solution {
public:
    int fourSumCount(vector<int>& nums1, vector<int>& nums2, vector<int>& nums3, vector<int>& nums4) {
        unordered_map<int, int> umap;
        for(int n1:nums1)
        {
            for(int n2:nums2)
            {
                umap[n1 + n2]++;
            }
        }

        int cnt = 0;
        for(int n3:nums3)
        {
            for(int n4:nums4)
            {
                if(umap.find(-(n3 + n4)) != umap.end())
                {
                    cnt += umap[-(n3 + n4)];
                }
            }
        }
        return cnt;
    }
};

代码思路：

此题跟第六天的两数之和有异曲同工之妙，思路是进行分组，将四个vector分成两组，通过 $O(N^{2})$ 复杂度的遍历，得到两个组的和，然后再通过unordered_map查找有无符合要求结果。其中unordered_map的key表示的是两个vector的和，value表示的是两个vector的所求的元素和的次数。

二、LeetCode383.赎金信

数组哈希表法：

class Solution {
public:
    bool canConstruct(string ransomNote, string magazine) {
        int cNum[26] = {0};
        if(ransomNote.size() > magazine.size())
            return false;
        
        for(int i = 0; i < magazine.size(); i++)
        {
            cNum[magazine[i] - 'a']++;
        }
        for(int i = 0; i < ransomNote.size(); i++)
        {
            if(cNum[ransomNote[i] - 'a'] == 0)
            {
                return false;
            }
            cNum[ransomNote[i] - 'a']--;
        }
        
        return true;
    }
};

代码思路：

题目本质就是两数组的字符比较，只要第二个数组中所有字符数都大于等于第一个数组的字符数，就返回true，否则返回false，其中正好可以遍历字符后保存字符出现的次数这一思想，所以可以采用哈希表法，而字母只有26个固定的，所以直接用数组即可。

三、LeetCode15.三数之和

双指针法：

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        
        int fast = 0;
        int slow = 0;
        vector<vector<int>> ret;
        // 1.先对数组进行排序
        sort(nums.begin(), nums.end());
        
        // 2.采用双指针法遍历
        for(int i = 0; i < nums.size(); i++)
        {
            if(nums[i] > 0)
                return ret;
            
            // 3.去重操作Ⅰ
            if (i > 0 && nums[i] == nums[i - 1]) {
                continue;
            }
            
            slow = i + 1;
            fast = nums.size() - 1;
            while(fast > slow)
            {
                if(nums[i] + nums[fast] + nums[slow] > 0)
                {
                    fast--;
                }
                else if(nums[i] + nums[fast] + nums[slow] < 0)
                {
                    slow++;
                }
                else
                {
                    ret.push_back(vector<int>{nums[i], nums[slow], nums[fast]});
                    // 4.去重操作Ⅱ
                    while(fast > slow && nums[fast] == nums[fast - 1])
                    {
                        fast--;
                    }
                    while(fast > slow && nums[slow] == nums[slow + 1])
                    {
                        slow++;
                    }

                    //找到答案时，指针收缩
                    fast--;
                    slow++;
                }
                
            }
        }   
        return ret;

    }
};

代码思路：

这道题采用双指针法的难点在于怎么进行去重，这点放在“代码细节注意”上讲解，首先我们要讲解最基本的遍历和运算，这道题是求和为0的三元组(a, b, c)，即a+b+c = 0。为了方便使用双指针法，还需要对数组进行排序。假设排序后当前数组内容是{-1, -1, -1, 0, 0, 1, 1, 2}，在第一次循环时，i，slow，fast的状态如下图：

每一层循环都会让slow=i-1,fast=nums.size()-1。那么当(nums[i] + nums[slow] + nums[fast])的值小于0，说明当前的和比较小，此时我们让slow向后移动来使得三元组的和变大。如果(nums[i] + nums[slow] + nums[fast])的值大于0，我们就向前移动fast让三元组的和变小。然后当slow不小于fast时，这一层循环结束，让i++进入下一层循环。这就是最基本的循环计算。

代码细节注意：

①首先使用双指针法之前要先对数组进行排序，为了方便slow和fast的指针移动。

②当nums[i] > 0时，即代表三元组(nums[i], nums[slow], nums[fast])的最小值nums[i]都大于0，所以三元组的和一定大于0，无论slow和fast怎么移动，都得不到和为0的三元组。

③去重操作Ⅰ：去重操作为什么会进行nums[i] == nums[i - 1]的条件判断？

假设有如下图所示的数组：

此时的三元组(nums[i], nums[slow], nums[fast])的和已经等于0了，所以我们可以直接把这个三元组记录下来，即当前的ret = {(-1, -1, 2)}，且接下来移动slow和fast一定会变成接下来的状态：

此时的三元组之和也为0，所以也可以记录下来，即ret此时的内容为{(-1, -1, 2), (-1, 0, 1)}。然后第一层循环结束， i 向后移动，得到下面状态：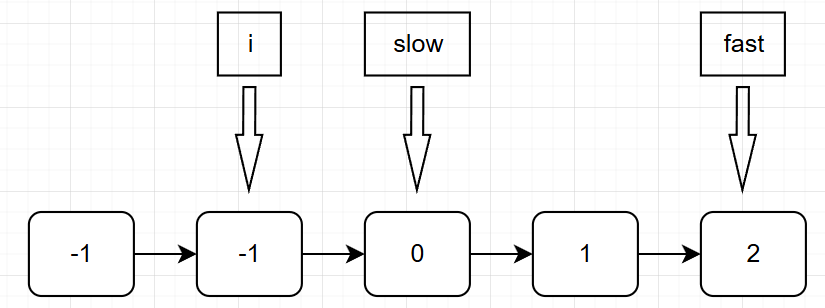

这时可以看到，如果nums[i] = nums[i - 1]的话，后续slow和fast的移动还会得到相同的三元组，即(-1, 0, 1)，这与之前得到的三元组重复了，所以当nums[i] = nums[i - 1]时，我们直接continue退出这次循环即可。

④去重操作Ⅱ：为什么还要用两个while对slow和fast所值元素进行去重呢？

假设数组的初始状态如下：

当我们得到第一个三元组（-1，-1，2）后，slow的下一个元素仍然是-1，而fast的前一个元素仍然是2，如果我们没有进行while来让slow和fast持续移动，而是只执行slow++和fast--的话就有可能出现下面这种错误情况：

最终我们又得到了一个与之前三元组重复的三元组（-1，-1，2），所以我们还需要对slow和fast位置元素也进行去重操作。即执行了while后再执行slow++和fast--。可以得到正确的状态：

四、LeetCode18.四数之和

题目链接： 18. 四数之和 - 力扣（LeetCode）

代码：

class Solution {
public:
    vector<vector<int>> fourSum(vector<int>& nums, int target) {
        int slow = 0;
        int fast = 0;
        sort(nums.begin(), nums.end());
        vector<vector<int>> ret;

        for(int i = 0; i < nums.size() - 1; i++)
        {
            // 剪枝操作
            if(nums[i] > target && nums[i] >= 0)
            {
                break;
            }
            // 去重操作
            if(i > 0 && nums[i] == nums[i - 1])
                continue;
            
            for(int k = i + 1; k < nums.size(); k++)
            {
                // 剪枝操作
                if(nums[k] + nums[i] > target && nums[k] + nums[i] >= 0)
                {
                    break;
                }
                //去重操作
                if(k > i + 1 && nums[k] == nums[k - 1])
                    continue;

                slow = k + 1;
                fast = nums.size() - 1;
                while(slow < fast)
                {
                    if((long)nums[i] + nums[k] + nums[slow] + nums[fast] > target) 
                        fast--;
                    else if((long)nums[i] + nums[k] + nums[slow] + nums[fast] < target)
                        slow++;
                    else
                    {
                        ret.push_back(vector<int>{nums[i], nums[k], nums[slow], nums[fast]});
                        while(slow < fast && nums[slow] == nums[slow + 1]) slow++;
                        while(slow < fast && nums[fast] == nums[fast - 1]) fast--;

                        slow++;
                        fast--;
                    }
                }
                
            }
        }
        return ret;
    }
};

代码思路：

跟三数之和一样的写法，但是多了一层for循环，并且两层for循环里面都进行了对应的剪枝操作和去重操作。